LoginSignup
3
5

More than 3 years have passed since last update.

@code0327(T Wada)

Pythonによる単回帰分析入門（数値計算/数式処理系の6ライブラリの比較）

Posted at

概要

Pythonで単回帰分析をしたいとき、つまり、回帰直線を求めたいとき、それを簡単に叶えてくれるライブラリが複数用意されています。ここでは「numpy」「scipy」「scikit-learn」「statsmodels」「sympy」「tensorflow」の6つライブラリを使って回帰直線（$y=ax+b$ のパラメータ $a$ と $b$）を求めるための方法／コードについて比較・整理をしました。

また、おまけとしてデータ可視化ライブラリ「seaborn」で自動描画される回帰直線から強引に回帰式パラメータを求める方法についても記載しました。

コードの動作確認は、GoogleColab.（Python 3.6.9）により行なっています。

準備

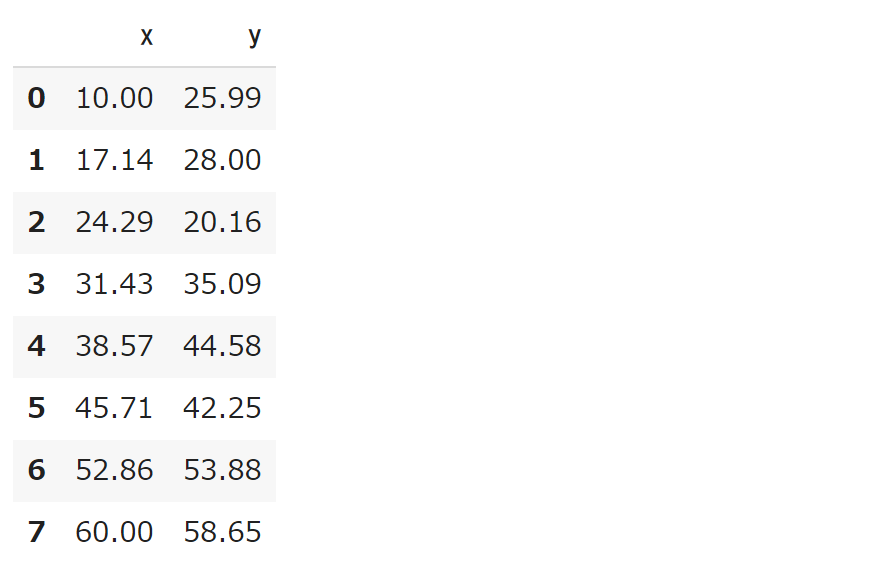
各種ライブラリをインポートをします。そして、一次関数 $8x+10$ に対して、正規分布 $N(0,6^2)$ に従う乱数 $\varepsilon$ を加えた $y=8x+10+\varepsilon$ からサンプルデータ（$8$個のセット）を生成します。

データの準備
import numpy as np
import pandas as pd
import scipy
import sklearn.linear_model
import statsmodels
import sympy
import tensorflow as tf
import matplotlib.pyplot as plt
import seaborn as sns

np.random.seed(10) # ランダムシートの固定
n = 8
x_range = (10,60)
x = np.round(np.linspace(*x_range,n),2)
e = np.random.normal(0,6,n)
y = np.round(0.8 * x + 10 + e,2)
df = pd.DataFrame({'x':x,'y':y})
display(df)

実行結果は、次のようになります。
2020-12-29_21h15_28.png

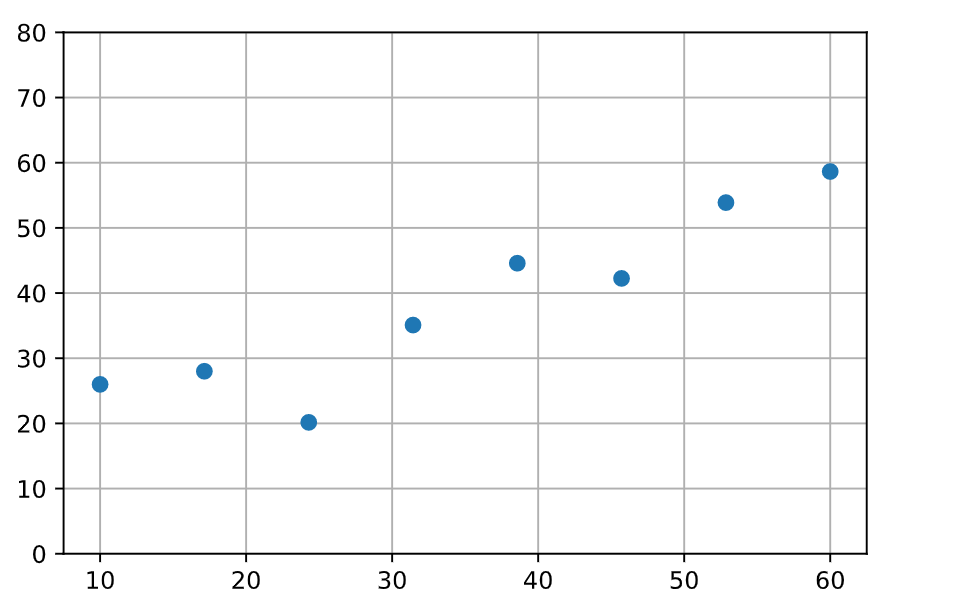
このデータを、matplotlib でプロットしていきます。

データのプロット
fig,ax = plt.subplots(1,1)
ax.scatter(x,y)
ax.set_ylim(0,80)       # Y軸の描画範囲
ax.grid()               # グリッドをオン
ax.set_axisbelow(True)  # グリッドを背面に移動
plt.show()              # 出力セルに描画

実行結果は、次のようになります。
2020-12-29_21h18_29.png

上記にプロットしたデータ（入力 $x$、出力 $y$）に対して、回帰式 $y=ax+b$ のパラメータ $a$ を $b$ を求めていきます。

回帰分析：statsmodels 編

statsmodels.formula.api.ols(...) を利用して回帰式を求めます。

statsmodels
print(f'> statsmodels {statsmodels.__version__}')
c = statsmodels.formula.api.ols(formula='y ~ x',data=df).fit()
print(f'a = {c.params["x"]:.2f}')
print(f'b = {c.params["Intercept"]:.2f}')
実行結果
> statsmodels 0.10.2
a = 0.72
b = 13.27

また、上記につづけて、print(c.summary()) とすれば、決定係数やパラメータの信頼区間といった情報を確認することができます。

c.summary()
                            OLS Regression Results                            
==============================================================================
Dep. Variable:                      y   R-squared:                       0.856
Model:                            OLS   Adj. R-squared:                  0.832
Method:                 Least Squares   F-statistic:                     35.69
Date:                Tue, 29 Dec 2020   Prob (F-statistic):           0.000987
Time:                        12:32:03   Log-Likelihood:                -23.986
No. Observations:                   8   AIC:                             51.97
Df Residuals:                       6   BIC:                             52.13
Df Model:                           1                                         
Covariance Type:            nonrobust                                         
==============================================================================
                 coef    std err          t      P>|t|      [0.025      0.975]
------------------------------------------------------------------------------
Intercept     13.2717      4.676      2.838      0.030       1.830      24.713
x              0.7230      0.121      5.974      0.001       0.427       1.019
==============================================================================
Omnibus:                        5.195   Durbin-Watson:                   2.078
Prob(Omnibus):                  0.074   Jarque-Bera (JB):                1.759
Skew:                          -1.142   Prob(JB):                        0.415
Kurtosis:                       3.242   Cond. No.                         91.3
==============================================================================

回帰分析：scikit-learn 編

sklearn.linear_model.LinearRegression() を利用して回帰式を求めます。単回帰の場合であっても、入力は行列（ndim=2）にして与える必要があります。今回の場合であれば、X.shape が (8,) ではダメで、(8,1) に変形しないといけません。

scikit-learn
print(f'> sklearn {sklearn.__version__}')
X = df['x'].values.reshape(len(df),1) # X.shape -> (8,1)
y = df['y'].values                    # y.shape -> (8,)
lr = sklearn.linear_model.LinearRegression()
lr.fit(X,y)
print(f'a = {lr.coef_[0]:.2f}')
print(f'b = {lr.intercept_:.2f}')
実行結果
> sklearn 0.22.2.post1
a = 0.72
b = 13.27

回帰分析：numpy 編

numpy.polyfit(...) を利用して回帰式を求めます。

numpy
print(f'> numpy {np.__version__}')
x = df['x'].values
y = df['y'].values
c = np.polyfit(x,y,1)
print(f'a = {c[0]:.2f}')
print(f'b = {c[1]:.2f}')
実行結果
> numpy 1.19.4
a = 0.72
b = 13.27

回帰分析：scipy 編

scipy.optimize.leastsq(...) あるいは scipy.optimize.curve_fit(...) を利用して回帰式を求めます。

scipy.optimize.leastsq(...)
print(f'> scipy {scipy.__version__}')
x = df['x'].values
y = df['y'].values
c = scipy.optimize.leastsq(lambda c,x,y:y-(c[0]*x+c[1]),(0,0),args=(x,y))
print(f'a = {c[0][0]:.2f}')
print(f'b = {c[0][1]:.2f}')
scipy.optimize.curve_fit(...)
print(f'> scipy {scipy.__version__}')
x = df['x'].values
y = df['y'].values
c = scipy.optimize.curve_fit(lambda x,a,b:a*x+b,x,y)
print(f'a = {c[0][0]:.2f}')
print(f'b = {c[0][1]:.2f}')

実行結果は、いずれも同じで次のようになります。

実行結果
> scipy 1.4.1
a = 0.72
b = 13.27

回帰分析：sympy 編

sympyは数値計算ではなく、数式処理のライブラリになります。よって、最小二乗法に基づく解析解を求めることができます。

コードのなかの J は、次のように残差の平方和（最小二乗法における最小化対象）になります。

$$ J(a,b) = \sum_{i=1}^{n}\left( y - ( ax+b ) \right)^2$$

また dJa と dJb は、それぞれ $J(a,b)$ の偏微分の解析解です。また、eq1 と eq2 は、次のように、それらをイコールゼロとした方程式になります。

$$ \frac{\partial J(a,b)}{\partial a}=0,\ \ \ \frac{\partial J(a,b)}{\partial b}=0 $$

そして、sympy.solve((eq1,eq2),(a,b)) で、これらの連立方程式を解いています。

sympy
print(f'> sympy {sympy.__version__}')
rx = df['x'].values
ry = df['y'].values

a, b = sympy.symbols('a,b')
n = sympy.symbols('n', integer=True, positive=True)
i = sympy.Idx('i')
x = sympy.IndexedBase('x')
y = sympy.IndexedBase('y')

xi = [ (x[i+1],rx[i]) for i in range(len(rx)) ]
yi = [ (y[i+1],ry[i]) for i in range(len(ry)) ]

J = sympy.Sum((y[i]-(a*x[i]+b))**2,(i,1,n)) # 残差平方和

dJa = sympy.diff(J,a) # aで偏微分
dJb = sympy.diff(J,b) # bで偏微分

dJa = dJa.subs(n,len(df)).doit().subs(xi).subs(yi) # xi,yiの代入
dJb = dJb.subs(n,len(df)).doit().subs(xi).subs(yi) # xi,yiの代入

eq1, eq2 = sympy.Eq(dJa,0), sympy.Eq(dJb,0) # 連立方程式を解く

r = sympy.solve((eq1,eq2),(a,b))
print(f'a = {float(r[a].subs(xi,yi)):.2f}')
print(f'b = {float(r[b].subs(xi,yi)):.2f}')
実行結果
> sympy 1.1.1
a = 0.72
b = 13.27

回帰分析：tensorflow 編

TensorFlow（2.X）の低レイヤの関数 tf.GradientTape(...) を使った勾配降下法により、回帰分析を行ないます。いい感じの結果を得るためには、学習率や反復回数などの調整が必要です。

tensorflow
print(f'> tensorflow {tf.__version__}')

x = df['x'].values
y = df['y'].values

a = tf.Variable(0.)
b = tf.Variable(0.)

for i in range(50000):
  with tf.GradientTape() as tape:
    y_pred = a*x+b
    loss = tf.math.reduce_mean(tf.square(y_pred-y))
  gradients = tape.gradient(loss,[a,b])
  a.assign_sub(0.0005 * gradients[0]) # 学習率 0.0005
  b.assign_sub(0.0005 * gradients[1])

  if (i + 1) % 10000 == 0:
    print(f'Step:{i+1} a = {a.numpy():.2f} b = {b.numpy():.2f}')

print(f'a = {a.numpy():.2f}')
print(f'b = {b.numpy():.2f}')
実行結果
> tensorflow 2.4.0
Step:10000 a = 0.77 b = 11.07
Step:20000 a = 0.73 b = 12.90
Step:30000 a = 0.72 b = 13.21
Step:40000 a = 0.72 b = 13.26
Step:50000 a = 0.72 b = 13.27
a = 0.72
b = 13.27

回帰分析：seaborn 編（おまけ）

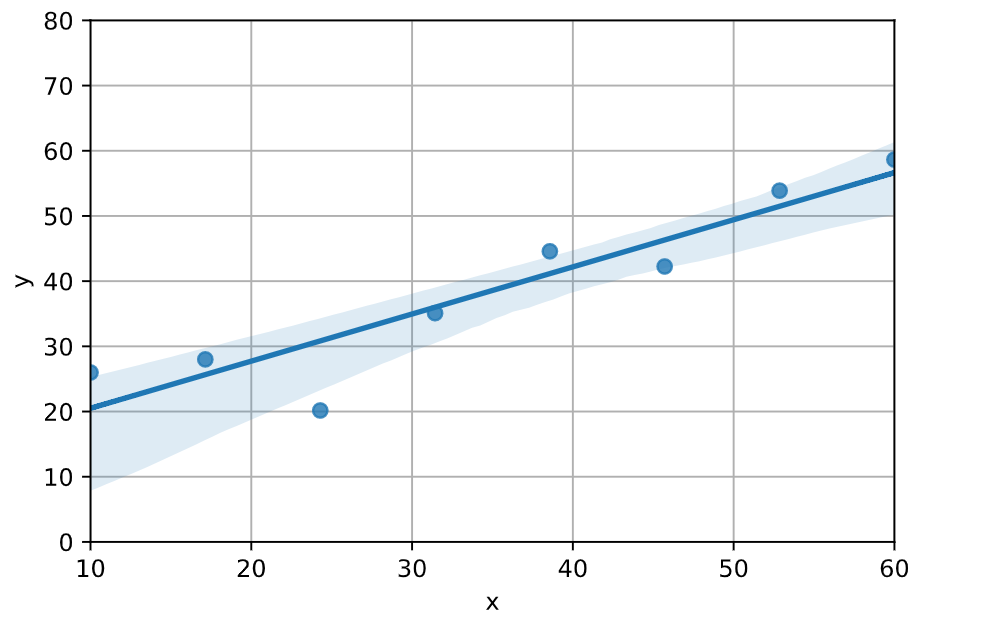
可視化ライブラリ seaborn.regplot(...) では、次のように回帰直線と$95\%$信頼区間をデフォルトで描画してくれます。

2020-12-29_22h50_31.png

しかし残念ながら、それら回帰直線や信頼区間のパラメータを参照する手段は用意されていないようなのです（参考）。そこで、回帰直線のプロットデータを取得し、そこから式のパラメータを計算することができます。

seaborn
print(f'> seaborn {sns.__version__}')
fig,ax = plt.subplots(1,1)
d = sns.regplot(x='x', y='y', data=df, ax=ax) # プロットデータの取得
ax.set_ylim(0,80)
ax.grid() 
ax.set_axisbelow(True)
plt.show()

xr = d.get_lines()[0].get_xdata() # 図内の回帰直線のXデータ
yr = d.get_lines()[0].get_ydata() # 図内の回帰直線のYデータ
a = (yr[-1]-yr[0])/(xr[-1]-xr[0])
b = yr[0]-a*xr[0]
print(f'a = {a:.2f}')
print(f'b = {b:.2f}')

実行結果は、次のようになります。

実行結果
> seaborn 0.11.0
a = 0.72
b = 13.27

参考

3
5
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
3
5