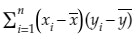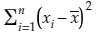はじめに
数理的な分野への適用を重視したブロック型のビジュアル･プログラミング･エディタであるところのK3Tunnel。
「数理的分野」のひとつの例として「本の厚さと重さ」の関係を表す直線の式を最小二乗法を使って求める例を紹介しています。初歩的な機械学習の例でもあり、やや骨太な内容になっています。正直言うと、この内容で最小二乗法で直線の式を決めるだけなら、Excelのグラフでちょろっとやればいいんじゃないの？という気もしますが、その裏で何をしているのか見えるようにしていきたいと思います。
なお、プログラムコードは、Loquatのエンジニアの方に協力していただいて作成しました。
プログラム例
ものはコチラです。
https://k3tunnel.com/k3t/sampleWork.html?sampleId=A0027
使うデータ
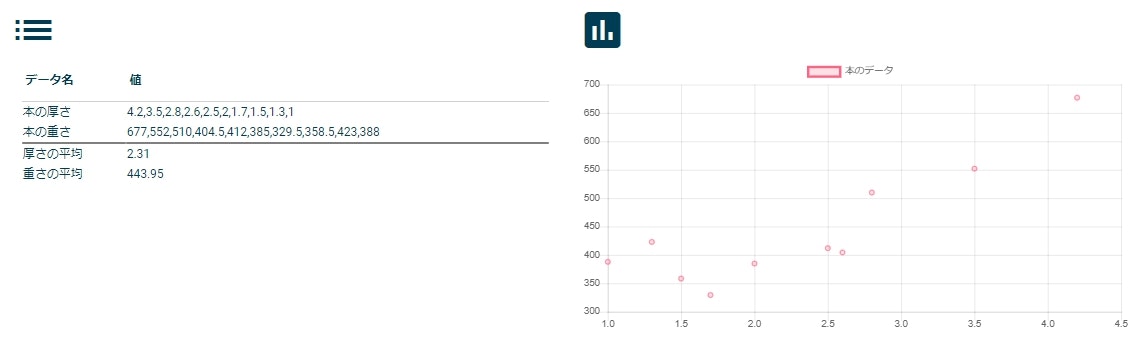
本の厚さと重さの実データから、その関係を表す式を求めていきます。
| 書籍名 | 厚さ[cm] | 重さ[g] |
|---|---|---|
| 謎の独立国家ソマリランド | 4.2 | 677 |
| 天地明察 | 3.5 | 552 |
| FACTFULNESS | 2.8 | 520 |
| フーガはユーガ | 2.6 | 404.5 |
| ライフロング・キンダーガーテン | 2.5 | 412 |
| 鳥類学者無謀にも恐竜を語る | 2 | 385 |
| ゾンビ対数学 | 1.7 | 329.5 |
| 鉄と鉄鋼がわかる本 | 1.5 | 358.5 |
| ルビィの冒険 | 1.3 | 423 |
| へんしんトンネル | 1 | 388 |
上記データは、すべて実測値です。
重さをはかっているところ。
厚さはかなりアバウトです。
こんな感じで地道に10冊すべて測定しました。
とりあえず実行してみる
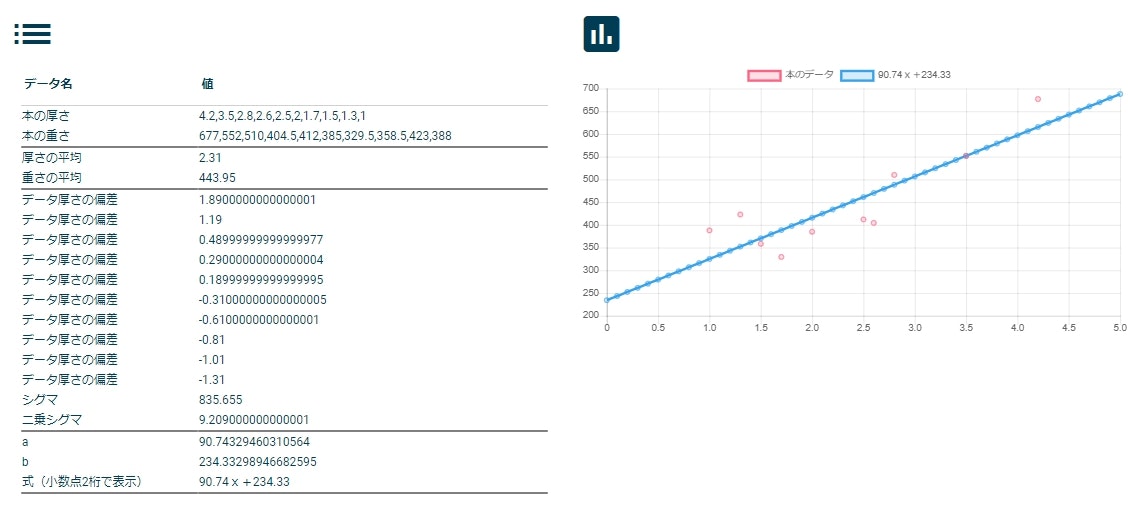
何をともあれ、実行してみると、こうなります。
右のグラフは、ピンクの〇が実データ。青い線が、プログラムで求めた式の直線。
左の表は、まあ、いろいろです。
コードを上から眺めていきます
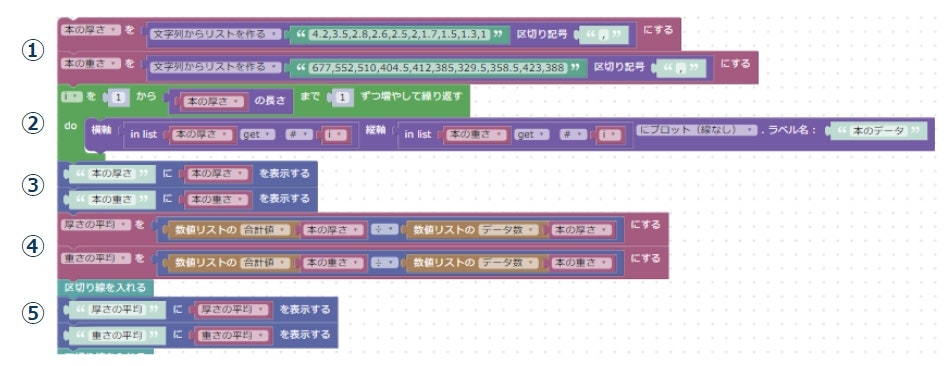
前半は、実データを確認しているだけ
まずはこの部分。
みたまんまですが、ざっくりまとめるとこんな感じ。
- 本の厚さと本の重さのリストを作って変数に入れる。
- 横軸を本の厚さ、縦軸を本の重さにしたグラフにデータをプロットしていく。
- リストの内容を表に出力。
- 厚さと重さの平均を計算。（合計値÷データ数）
- 計算した平均値を表に出力
ここまでで実行するとこう。
ここまでは、K3Tunnelのクセはあるものの、特に難しいことはしていません。
このあと、シグマだの偏差だの出てくるので、いったんコードから離れます。
このプログラムのゴール
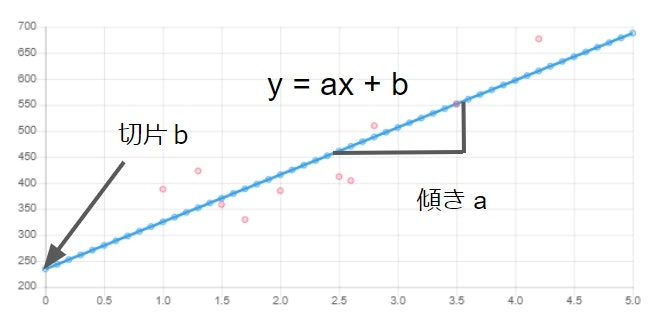
直線を表す数式を求めたい
直線を表す式が、y = ax + bであることは、中学生のときに習いました。ここでは、yが本の重さ、xが本の厚さということになります。未知のパラメータa, bを決めてこの式を求める。というのが、このプログラムのゴールです。
a, bを求める数式
最小二乗法を使うと、a, bは、以下の式で表すことができます。
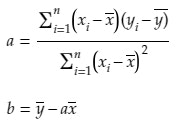
なぜこうなるかは、おいておいて、この式を使ってa, bを計算します。
Σは全部足す。文字の上に線があるやつは、平均値という意味です。
aを求める数式を日本語にする
今回の問題設定にあわせて、aを求める数式を日本語にしてみます。
まずは分子から
- すべての本について、
(本の厚さ - 厚さの平均）× (本の重さ - 重さの平均)を計算する - 上で求めた数値を全部足す
プログラム例では、この値を**「偏差のシグマ」**と呼んでいます。
次は分母
- すべての本について、
(本の厚さ - 厚さの平均）の二乗を計算する - 上で求めた数値を全部足す
プログラム例では、この値を**「偏差の二乗シグマ」**と呼んでいます。
最終的にaは以下で求められます。
bを求める数式を日本語にする
bを求める数式も、一応、日本語にしておきます。
b = (重さの平均）- a × (厚さの平均)
aの分母と分子をそれぞれ計算する
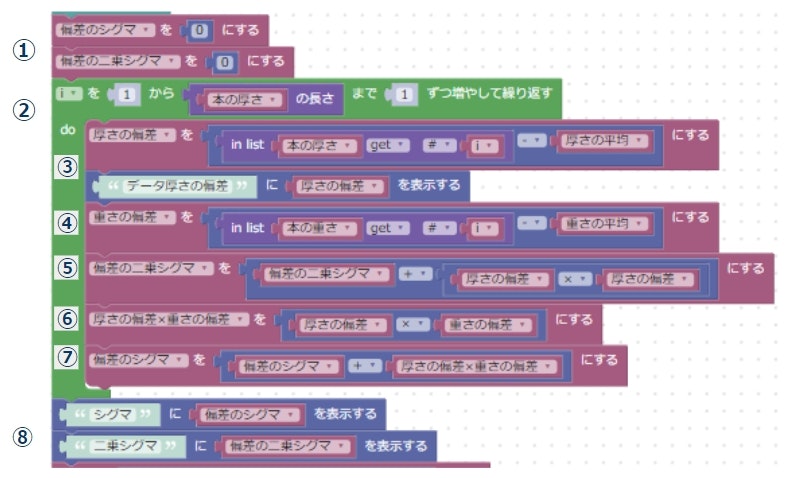
プログラムに戻ります。
リストに入れたデータをひとつずつ取り出してきて、「偏差の二乗シグマ」と「偏差のシグマ」を計算しています。
見たまんまですが、日本語にするとこんな感じ。
- 変数を初期化
- 本のデータの1番目から最後まで③から⑦までの処理を繰り返す
-
(本の厚さ - 厚さの平均）を計算して「厚さの偏差」とする -
(本の重さ - 重さの平均）を計算して「重さの偏差」とする - 「偏差の二乗シグマ」変数に
「厚さの偏差」の二乗を足していく（繰り返しのたびに値が増える） - 「厚さの偏差」× 「重さの偏差」を計算する
- 「偏差のシグマ」変数に
「厚さの偏差」×「重さの偏差」を足していく（繰り返しのたびに値が増える） - 「偏差の二乗シグマ」と「偏差のシグマ」を表に出力する
ここまでで、a を求める用意ができました。
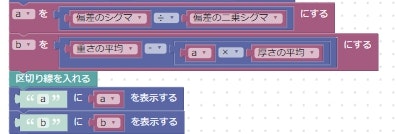
a,b を計算する
その次は、計算式に代入した結果を、表出力しているだけです。
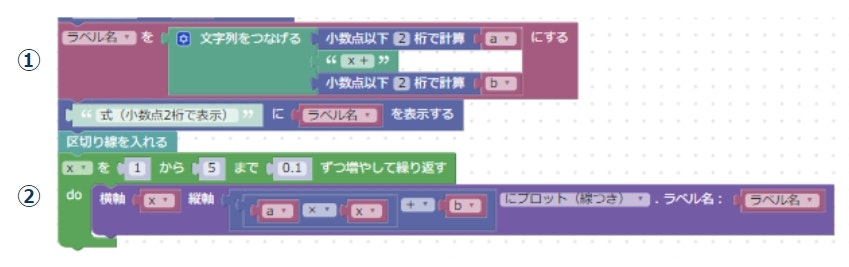
もとめた直線をかく
最後のパート。表示するためにごちゃごちゃやっています。
- y = ax + b の形で表示するために文字列操作。
- 式に値を代入して、グラフにプロットして線をつなぐ。
完成
この式を使えば、「厚さを測れば、重さを推定できるようになる。(似たような紙質であれば)」というわけです。紙質まで考慮しようとすると、どーんと難しくなりますが、それは、また別のお話。
自分でいろいろやってみるには
プログラム例の画面にて、「コピーしてプロジェクト作成」すると、編集できるようになります。プログラム例の画面ではブロックを動かすこともできません。。
これをクリックしたのち、確認画面で「新規作成」をクリックすると編集画面に移ります。
おわりに
自分で最小二乗法を実装することは、もうないような気がします。