Atcoderで使える! pythonで優先付きキュー 【ABC137 D問題】

はじめに

8月10日21時開催の AtCoder Beginner Contest 137のD問題が良問で、勉強になったので、解法も含め記事にまとめます。

問題

問題は以下の通りでした。

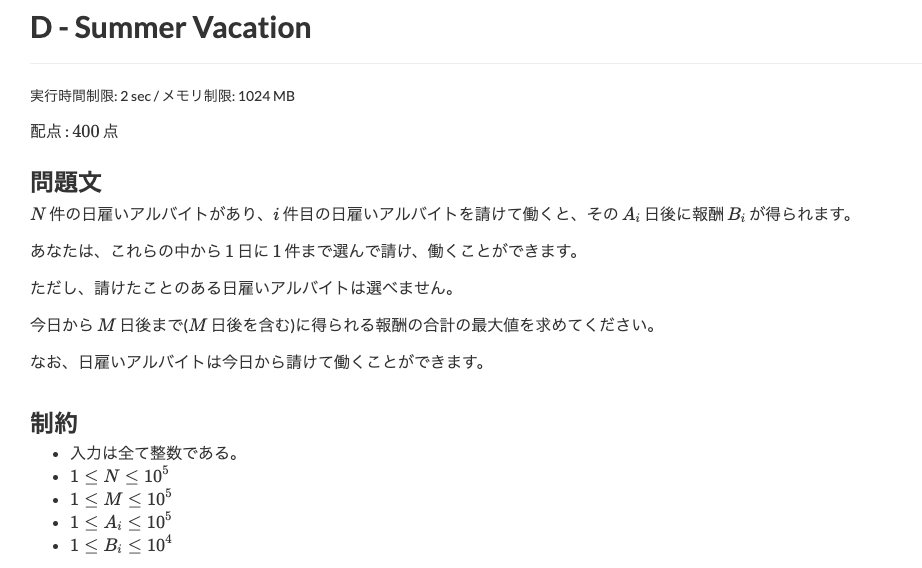
(https://atcoder.jp/contests/abc137/tasks/abc137_d)

一見、ナップサック問題のような印象を受け、最適解求めることできるのかよ。。。と思いましたが少し考えたのち、以下のような方針で最適解が導出可能であることがわかりました。

方針

公式の解説がまんまだったので、引用させて頂きます。

(https://img.atcoder.jp/abc137/editorial.pdf)

• 候補の追加
• 候補の中から最大値を取り出す
• 以下、条件を満たすまで繰り返し

Atcoderでは上記を実装したい場面が度々訪れますよね、、今回、私ははじめ、単純に以下のようなコードを書いて実装しました。
とりあえずリストに追加して、毎回max関数を呼び出しているため、計算量がえげつない事になり、**TLE(実行時間超過)**でした。

今回の問題のような場合では、優先付きキューを使うと高速に計算が可能です。

# 標準入力受け取り
N, M = list(map(int, input().split()))
jobs = [[] for _ in range(M)]

for i in range(N):
    d, r = list(map(int, input().split()))
    if d-1 < M:
        jobs[d-1].append(r)

# 解法
rewards = 0
li = []
for i in range(M):
    #候補をリストに追加(給料が間に合うもの仕事が一日ごとに増える)
    li.extend(jobs[i])
    if len(li) >0:
        #最大値を求める(給料が高いバイトをしたい)
        reward = max(li)
        rewards += reward
        #使った値は取り除く(同じバイトはNGのため)
        li.remove(reward)
    
print(rewards)

優先付きキュー

https://ufcpp.net/study/algorithm/col_heap.html を見ると完全に理解できます。
簡単にまとめると**ヒープ(heap)**という2分木を利用する事で、追加、取り出し操作を最大でも木の深さ回で実行可能な手法です。

pythonで実装する際にはheapqというモジュールがあるので利用し、コードを改良しました。
(ただし、heapqはMin heapのみ対応しているため全ての値にマイナスを付け反転させて利用しました)
この実装により無事に**AC(正答)**をゲットしました。

import heapq
# 標準入力受け取り
N, M = list(map(int, input().split()))
jobs = [[] for _ in range(M)]

for i in range(N):
    d, r = list(map(int, input().split()))
    if d-1 < M:
        jobs[d-1].append(-r) #マイナスにしている

rewords = 0
heap = []

# 解法
for i in range(M):
    print(jobs[:i])
    #要素を一つづつヒープに追加
    for reword in jobs[i]:
        heapq.heappush(heap, reward)
    if len(heap) >0:
        #最大値(最小値)をヒープから取り出し
        reword = heapq.heappop(heap)
        print(r)
        rewards += -reword#マイナスにしている

print(rewards)

まとめ

• Atcoderにおいて、データ数が多い場合には、とりあえずリストに追加はTLEの餌食
• リストで何をしたいか考えてそれにあったデータ構造にすべし
• 追加、最大(小)値取り出しの繰り返しにはヒープを用いた優先付きキュー