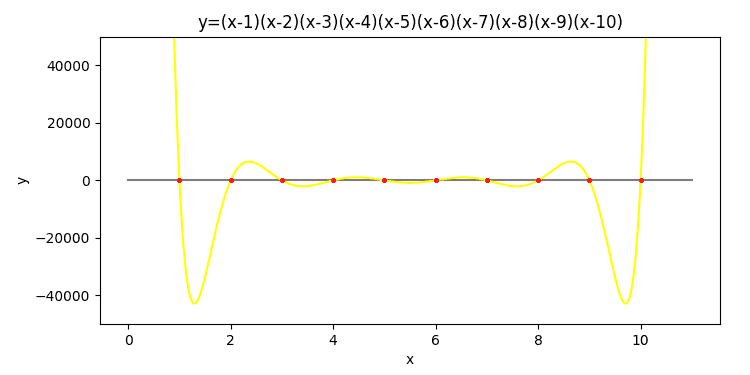
解の検証
前回の4台クラスターで、高次方程式を解く I (重解なし)では、4台のRaspberry Pi4Bクラスターを使い、上図のような10次方程式(重解なし)を解くプログラムを作りました。(上図グラフはmatplotlib 3.3.3で描いています)今回は続編または付録です。ただ今回使用するRaspberry Pi4Bは1台だけです。そして前回は10次でしたが、今回は100次方程式(重解なし)を解くプログラムを作ります。
まず最初に、前回やり残していた解の検証を増設し、10次方程式(重解なし)を解くプログラムを完成させました。xの2点間でy値の符号が変わる点(x軸を横切る点)を解とするシンプルな判定法です。プログラム的な変更点は、高速化の@jitと4 coreマルチプロセッシングを追加しました。numbaの@jitは、Raspberry OS with Desktop添付のオリジナルpythonプログラムで書いたシンプルな関数前に@jitを1行追加するだけで高速化します。ローカルリストが使えます。ただし1次元リストは使えるが2次元リストは使えない。グローバル変数およびリストは使えない。またnumpyのコードを使って高速化コーディングしていると逆にエラーが出る。プログラム作成途上、エラーがたくさん出たのですが、今回のプログラムはnumbaの@jitで使える(2021JAN04現在)、ローカル1次元リスト,append,forループ,if条件文,args引数リスト受取,return結果リスト返却というシンプルな構成で関数を書いています。導入時の詳細は前回の基本オプション@njitおよびmultiprocessingを見てください。今回のプログラムを下に添付しています。
import time
from multiprocessing import Pool
# from numba import njit
# @njit(cache=True)
def calc_2s(i0,R_f,X_init,X_end,A0,A1,A2,A3,A4,A5,A6,A7,A8,A9,A10):
Ypre=0
totalsXY=[i0]
for x0 in range(int(X_init), int(X_end)+1):
X = x0/R_f
Y = A0+A1*(X)**1+A2*(X)**2+A3*(X)**3+A4*(X)**4+A5*(X)**5+\
A6*(X)**6+A7*(X)**7+A8*(X)**8+A9*(X)**9+A10*(X)**10
if x0==int(X_init):
Ypre=Y
if Ypre * Y > 0:
Ypre=Y
else:
if Y == 0.0:
totalsXY.append(X)
totalsXY.append(Y)
else:
Ypre=Y
totalsXY.append(X)
totalsXY.append(Y)
return totalsXY
def wrapper_func(args):
return calc_2s(*args)
def multi_processing_pool(Args_Lists):
p = Pool(4)
process_XY = p.map(wrapper_func, Args_Lists)
p.close()
return process_XY
if __name__=="__main__":
print(f"pre-cache")
x_Range_to = 12
r_f = 10
f_range = x_Range_to * r_f
a0=1.
a1=0.
a2=0.
a3=0.
a4=0.
a5=0.
a6=0.
a7=0.
a8=0.
a9=0.
a10=0.
ArgsLists= [(i,r_f,i*f_range/4,(i+1)*f_range/4,\
a0,a1,a2,a3,a4,a5,a6,a7,a8,a9,a10) for i in range(4)]
processXY = multi_processing_pool(ArgsLists)
processXY.clear()
print(f"Calculation Start")
x_Range_to = 12
r_f = 1000000
f_range = x_Range_to * r_f
a0 = 3628801.0
a1 =-10628640.0
a2 = 12753576.0
a3 =-8409500.0
a4 = 3416930.0
a5 =-902055.0
a6 = 157773.0
a7 =-18150.0
a8 = 1320.0
a9 =-55.0
a10= 1.0
initial_time=time.time()
ArgsLists= [(i,r_f,i*f_range/4,(i+1)*f_range/4,\
a0,a1,a2,a3,a4,a5,a6,a7,a8,a9,a10) for i in range(4)]
processXY = multi_processing_pool(ArgsLists)
print(f"Calculation Finished")
processXYstr = str(processXY)
processXYstr = processXYstr.replace('[[', '')
processXYstr = processXYstr.replace(']]', '')
processesXYstr=processXYstr.split('], [')
process0XYstr=processesXYstr[0]
process1XYstr=processesXYstr[1]
process2XYstr=processesXYstr[2]
process3XYstr=processesXYstr[3]
process0sXYstr=process0XYstr.split(', ')
process1sXYstr=process1XYstr.split(', ')
process2sXYstr=process2XYstr.split(', ')
process3sXYstr=process3XYstr.split(', ')
if process0sXYstr[0]=='0' or process0sXYstr[0]=='0.0':
ProcessAdatas=process0sXYstr.copy()
elif process1sXYstr[0]=='0' or process1sXYstr[0]=='0.0':
ProcessAdatas=process1sXYstr.copy()
elif process2sXYstr[0]=='0' or process2sXYstr[0]=='0.0':
ProcessAdatas=process2sXYstr.copy()
elif process3sXYstr[0]=='0' or process3sXYstr[0]=='0.0':
ProcessAdatas=process3sXYstr.copy()
if process0sXYstr[0]=='1' or process0sXYstr[0]=='1.0':
ProcessBdatas=process0sXYstr.copy()
elif process1sXYstr[0]=='1' or process1sXYstr[0]=='1.0':
ProcessBdatas=process1sXYstr.copy()
elif process2sXYstr[0]=='1' or process2sXYstr[0]=='1.0':
ProcessBdatas=process2sXYstr.copy()
elif process3sXYstr[0]=='1' or process3sXYstr[0]=='1.0':
ProcessBdatas=process3sXYstr.copy()
if process0sXYstr[0]=='2' or process0sXYstr[0]=='2.0':
ProcessCdatas=process0sXYstr.copy()
elif process1sXYstr[0]=='2' or process1sXYstr[0]=='2.0':
ProcessCdatas=process1sXYstr.copy()
elif process2sXYstr[0]=='2' or process2sXYstr[0]=='2.0':
ProcessCdatas=process2sXYstr.copy()
elif process3sXYstr[0]=='2' or process3sXYstr[0]=='2.0':
ProcessCdatas=process3sXYstr.copy()
if process0sXYstr[0]=='3' or process0sXYstr[0]=='3.0':
ProcessDdatas=process0sXYstr.copy()
elif process1sXYstr[0]=='3' or process1sXYstr[0]=='3.0':
ProcessDdatas=process1sXYstr.copy()
elif process2sXYstr[0]=='3' or process2sXYstr[0]=='3.0':
ProcessDdatas=process2sXYstr.copy()
elif process3sXYstr[0]=='3' or process3sXYstr[0]=='3.0':
ProcessDdatas=process3sXYstr.copy()
process0sXYstr.clear()
process0XYstr=''
process1sXYstr.clear()
process1XYstr=''
process2sXYstr.clear()
process2XYstr=''
process3sXYstr.clear()
process3XYstr=''
ProcessAdatas.pop(0)
ProcessBdatas.pop(0)
ProcessCdatas.pop(0)
ProcessDdatas.pop(0)
answersXY=[]
for i in range(int(len(ProcessAdatas)/2)):
answersXY.append((float(ProcessAdatas[2*i]),\
float(ProcessAdatas[2*i+1])))
for i in range(int(len(ProcessBdatas)/2)):
answersXY.append((float(ProcessBdatas[2*i]),\
float(ProcessBdatas[2*i+1])))
for i in range(int(len(ProcessCdatas)/2)):
answersXY.append((float(ProcessCdatas[2*i]),\
float(ProcessCdatas[2*i+1])))
for i in range(int(len(ProcessDdatas)/2)):
answersXY.append((float(ProcessDdatas[2*i]),\
float(ProcessDdatas[2*i+1])))
print(f"Time :")
print(str(time.time() - initial_time))
print(f"Answers :")
for i in range(len(answersXY)):
print(answersXY[i])
time.sleep(10)
100次方程式を解く(重解なし)
Raspberry Pi4Bを1台だけ使用して、100次方程式(重解なし)を解くプログラムを作成しました。今回もあらかじめ解の分かっている因数分解可能な式を使いました。
y=
(x- 0.950)(x- 0.951)(x- 0.952)(x- 0.953)(x- 0.954)×
(x- 0.955)(x- 0.956)(x- 0.957)(x- 0.958)(x- 0.959)×
(x- 0.960)(x- 0.961)(x- 0.962)(x- 0.963)(x- 0.964)×
(x- 0.965)(x- 0.966)(x- 0.967)(x- 0.968)(x- 0.969)×
(x- 0.970)(x- 0.971)(x- 0.972)(x- 0.973)(x- 0.974)×
(x- 0.975)(x- 0.976)(x- 0.977)(x- 0.978)(x- 0.979)×
(x- 0.980)(x- 0.981)(x- 0.982)(x- 0.983)(x- 0.984)×
(x- 0.985)(x- 0.986)(x- 0.987)(x- 0.988)(x- 0.989)×
(x- 0.990)(x- 0.991)(x- 0.992)(x- 0.993)(x- 0.994)×
(x- 0.995)(x- 0.996)(x- 0.997)(x- 0.998)(x- 0.999)×
(x- 1.000)(x- 1.001)(x- 1.002)(x- 1.003)(x- 1.004)×
(x- 1.005)(x- 1.006)(x- 1.007)(x- 1.008)(x- 1.009)×
(x- 1.010)(x- 1.011)(x- 1.012)(x- 1.013)(x- 1.014)×
(x- 1.015)(x- 1.016)(x- 1.017)(x- 1.018)(x- 1.019)×
(x- 1.020)(x- 1.021)(x- 1.022)(x- 1.023)(x- 1.024)×
(x- 1.025)(x- 1.026)(x- 1.027)(x- 1.028)(x- 1.029)×
(x- 1.030)(x- 1.031)(x- 1.032)(x- 1.033)(x- 1.034)×
(x- 1.035)(x- 1.036)(x- 1.037)(x- 1.038)(x- 1.039)×
(x- 1.040)(x- 1.041)(x- 1.042)(x- 1.043)(x- 1.044)×
(x- 1.045)(x- 1.046)(x- 1.047)(x- 1.048)(x- 1.049) = 0
1.00は100乗しても1.00です。1.00極近傍の数は100乗しても小数点より上の整数部の桁数が増えません。これよりpythonの倍精度浮動小数点の有効数字桁数をすべて小数点以下で使えます。今回は上のような100次方程式を用意しました。(小数点以下が小さ過ぎると、逆に少数以下の桁数が倍精度浮動小数点の桁数の圏外に外れるので、用意した式が最適かどうかはわからないですが)
この100次方程式を解くプログラムを次に示しました。計算する100次方程式が1.00極近傍にだけ解を持つという特殊性以外、前述の10次方程式でのプログラムとプログラム自体はほとんど同じです。(変数は10次方程式の時の11個から、100次方程式では100個に増えていますが)
import time
from multiprocessing import Pool
# from numba import njit
# @njit(cache=True)
def calc_2s(i0,x_Range_from,R_f,X_init,X_end,\
A0, A1, A2, A3, A4, A5, A6, A7, A8, A9,\
A10,A11,A12,A13,A14,A15,A16,A17,A18,A19,\
A20,A21,A22,A23,A24,A25,A26,A27,A28,A29,\
A30,A31,A32,A33,A34,A35,A36,A37,A38,A39,\
A40,A41,A42,A43,A44,A45,A46,A47,A48,A49,\
A50,A51,A52,A53,A54,A55,A56,A57,A58,A59,\
A60,A61,A62,A63,A64,A65,A66,A67,A68,A69,\
A70,A71,A72,A73,A74,A75,A76,A77,A78,A79,\
A80,A81,A82,A83,A84,A85,A86,A87,A88,A89,\
A90,A91,A92,A93,A94,A95,A96,A97,A98,A99):
totalsXY=[i0]
Ypre=0
for x0 in range(int(X_init), int(X_end)+1):
X = x_Range_from + (x0/R_f)
Y = (X -A0)*(X -A1)*(X -A2)*(X -A3)*(X -A4)*\
(X -A5)*(X -A6)*(X -A7)*(X -A8)*(X -A9)*\
(X-A10)*(X-A11)*(X-A12)*(X-A13)*(X-A14)*\
(X-A15)*(X-A16)*(X-A17)*(X-A18)*(X-A19)*\
(X-A20)*(X-A21)*(X-A22)*(X-A23)*(X-A24)*\
(X-A25)*(X-A26)*(X-A27)*(X-A28)*(X-A29)*\
(X-A30)*(X-A31)*(X-A32)*(X-A33)*(X-A34)*\
(X-A35)*(X-A36)*(X-A37)*(X-A38)*(X-A39)*\
(X-A40)*(X-A41)*(X-A42)*(X-A43)*(X-A44)*\
(X-A45)*(X-A46)*(X-A47)*(X-A48)*(X-A49)*\
(X-A50)*(X-A51)*(X-A52)*(X-A53)*(X-A54)*\
(X-A55)*(X-A56)*(X-A57)*(X-A58)*(X-A59)*\
(X-A60)*(X-A61)*(X-A62)*(X-A63)*(X-A64)*\
(X-A65)*(X-A66)*(X-A67)*(X-A68)*(X-A69)*\
(X-A70)*(X-A71)*(X-A72)*(X-A73)*(X-A74)*\
(X-A75)*(X-A76)*(X-A77)*(X-A78)*(X-A79)*\
(X-A80)*(X-A81)*(X-A82)*(X-A83)*(X-A84)*\
(X-A85)*(X-A86)*(X-A87)*(X-A88)*(X-A89)*\
(X-A90)*(X-A91)*(X-A92)*(X-A93)*(X-A94)*\
(X-A95)*(X-A96)*(X-A97)*(X-A98)*(X-A99)
if x0==int(X_init):
Ypre=Y
if Ypre * Y > 0:
Ypre=Y
else:
if Y == 0.0:
totalsXY.append(X)
totalsXY.append(Y)
else:
Ypre=Y
totalsXY.append(X)
totalsXY.append(Y)
return totalsXY
def wrapper_func(args):
return calc_2s(*args)
def multi_processing_pool(Args_Lists):
p = Pool(4)
process_XY = p.map(wrapper_func, Args_Lists)
p.close()
return process_XY
if __name__=="__main__":
''' INPUT START '''
x_range_from = 0.9
x_range_to = 1.1
r_f = 2000
a0 = 0.950
a1 = 0.951
a2 = 0.952
a3 = 0.953
a4 = 0.954
a5 = 0.955
a6 = 0.956
a7 = 0.957
a8 = 0.958
a9 = 0.959
a10= 0.960
a11= 0.961
a12= 0.962
a13= 0.963
a14= 0.964
a15= 0.965
a16= 0.966
a17= 0.967
a18= 0.968
a19= 0.969
a20= 0.970
a21= 0.972
a22= 0.972
a23= 0.973
a24= 0.974
a25= 0.975
a26= 0.976
a27= 0.977
a28= 0.978
a29= 0.979
a30= 0.980
a31= 0.981
a32= 0.982
a33= 0.983
a34= 0.984
a35= 0.985
a36= 0.986
a37= 0.987
a38= 0.988
a39= 0.989
a40= 0.990
a41= 0.991
a42= 0.992
a43= 0.993
a44= 0.994
a45= 0.995
a46= 0.996
a47= 0.997
a48= 0.998
a49= 0.999
a50= 1.000
a51= 1.001
a52= 1.002
a53= 1.003
a54= 1.004
a55= 1.005
a56= 1.006
a57= 1.007
a58= 1.008
a59= 1.009
a60= 1.010
a61= 1.011
a62= 1.012
a63= 1.013
a64= 1.014
a65= 1.015
a66= 1.016
a67= 1.017
a68= 1.018
a69= 1.019
a70= 1.020
a71= 1.021
a72= 1.022
a73= 1.023
a74= 1.024
a75= 1.025
a76= 1.026
a77= 1.027
a78= 1.028
a79= 1.029
a80= 1.030
a81= 1.031
a82= 1.032
a83= 1.033
a84= 1.034
a85= 1.035
a86= 1.036
a87= 1.037
a88= 1.038
a89= 1.039
a90= 1.040
a91= 1.041
a92= 1.042
a93= 1.043
a94= 1.044
a95= 1.045
a96= 1.046
a97= 1.047
a98= 1.048
a99= 1.049
''' INPUT END '''
print(f"Calculation Start")
initial_time=time.time()
f_range = (x_range_to - x_range_from) * r_f
ArgsLists= [(i,x_range_from,r_f,i*f_range/4,(i+1)*f_range/4,\
a0, a1, a2, a3, a4, a5, a6, a7, a8, a9,\
a10,a11,a12,a13,a14,a15,a16,a17,a18,a19,\
a20,a21,a22,a23,a24,a25,a26,a27,a28,a29,\
a30,a31,a32,a33,a34,a35,a36,a37,a38,a39,\
a40,a41,a42,a43,a44,a45,a46,a47,a48,a49,\
a50,a51,a52,a53,a54,a55,a56,a57,a58,a59,\
a60,a61,a62,a63,a64,a65,a66,a67,a68,a69,\
a70,a71,a72,a73,a74,a75,a76,a77,a78,a79,\
a80,a81,a82,a83,a84,a85,a86,a87,a88,a89,\
a90,a91,a92,a93,a94,a95,a96,a97,a98,a99) for i in range(4)]
processXY = multi_processing_pool(ArgsLists)
print(f"Calculation Finished")
processXYstr = str(processXY)
processXYstr = processXYstr.replace('[[', '')
processXYstr = processXYstr.replace(']]', '')
processesXYstr=processXYstr.split('], [')
process0XYstr=processesXYstr[0]
process1XYstr=processesXYstr[1]
process2XYstr=processesXYstr[2]
process3XYstr=processesXYstr[3]
if process0XYstr[0]=='0' or process0XYstr[0]=='0.0':
process0sXYstr=process0XYstr.split(', ')
elif process1XYstr[0]=='0' or process1XYstr[0]=='0.0':
process0sXYstr=process1XYstr.split(', ')
elif process2XYstr[0]=='0' or process2XYstr[0]=='0.0':
process0sXYstr=process2XYstr.split(', ')
elif process3XYstr[0]=='0' or process3XYstr[0]=='0.0':
process0sXYstr=process3XYstr.split(', ')
if process0XYstr[0]=='1' or process0XYstr[0]=='1.0':
process1sXYstr=process0XYstr.split(', ')
elif process1XYstr[0]=='1' or process1XYstr[0]=='1.0':
process1sXYstr=process1XYstr.split(', ')
elif process2XYstr[0]=='1' or process2XYstr[0]=='1.0':
process1sXYstr=process2XYstr.split(', ')
elif process3XYstr[0]=='1' or process3XYstr[0]=='1.0':
process1sXYstr=process3XYstr.split(', ')
if process0XYstr[0]=='2' or process0XYstr[0]=='2.0':
process2sXYstr=process0XYstr.split(', ')
elif process1XYstr[0]=='2' or process1XYstr[0]=='2.0':
process2sXYstr=process1XYstr.split(', ')
elif process2XYstr[0]=='2' or process2XYstr[0]=='2.0':
process2sXYstr=process2XYstr.split(', ')
elif process3XYstr[0]=='2' or process3XYstr[0]=='2.0':
process2sXYstr=process3XYstr.split(', ')
if process0XYstr[0]=='3' or process0XYstr[0]=='3.0':
process3sXYstr=process0XYstr.split(', ')
elif process1XYstr[0]=='3' or process1XYstr[0]=='3.0':
process3sXYstr=process1XYstr.split(', ')
elif process2XYstr[0]=='3' or process2XYstr[0]=='3.0':
process3sXYstr=process2XYstr.split(', ')
elif process3XYstr[0]=='3' or process3XYstr[0]=='3.0':
process3sXYstr=process3XYstr.split(', ')
process0sXYstr.pop(0)
process1sXYstr.pop(0)
process2sXYstr.pop(0)
process3sXYstr.pop(0)
answersXY=[]
for i in range(int(len(process0sXYstr)/2)):
answersXY.append((float(process0sXYstr[2*i]),\
float(process0sXYstr[2*i+1])))
for i in range(int(len(process1sXYstr)/2)):
answersXY.append((float(process1sXYstr[2*i]),\
float(process1sXYstr[2*i+1])))
for i in range(int(len(process2sXYstr)/2)):
answersXY.append((float(process2sXYstr[2*i]),\
float(process2sXYstr[2*i+1])))
for i in range(int(len(process3sXYstr)/2)):
answersXY.append((float(process3sXYstr[2*i]),\
float(process3sXYstr[2*i+1])))
print(f"Time :")
print(str(time.time() - initial_time))
print(f"Answers :")
for i in range(len(answersXY)):
print(answersXY[i])
time.sleep(10)
上のプログラム実行すると、解100個+候補100個が並びます。次図はmatplotlibで描いた今回の100次方程式のグラフです。matplotlibは100次方程式でも簡単に描きます。上側のグラフは0.950と1.050でx軸を横切っていることが分かります。中間は直線に見えます。100個の解があるはずなのですが何かわかりません。下側のグラフはy軸を拡大したものです。x軸を横切る上下動を繰り返しながらx=1.000で限りなく0に近づいています。確かにx軸を100回横切っています。
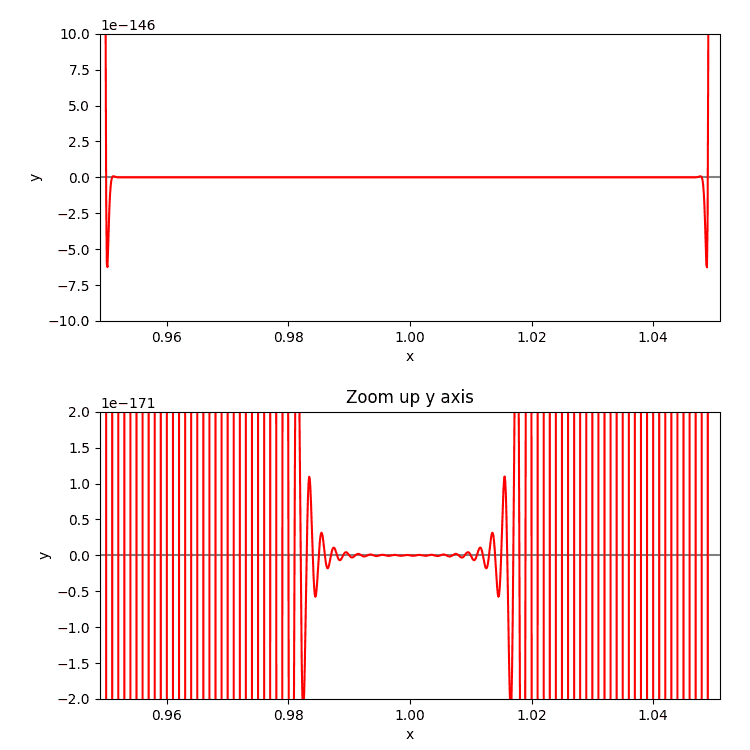
matplotlibはまったく初描画という段階で下のようなプログラムです。
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0.949, 1.051, 1000)
y = (x-0.950)*(x-0.951)*(x-0.952)*(x-0.953)*(x-0.954)*(x-0.955)*(x-0.956)*(x-0.957)*(x-0.958)*(x-0.959)*\
(x-0.960)*(x-0.961)*(x-0.962)*(x-0.963)*(x-0.964)*(x-0.965)*(x-0.966)*(x-0.967)*(x-0.968)*(x-0.969)*\
(x-0.970)*(x-0.971)*(x-0.972)*(x-0.973)*(x-0.974)*(x-0.975)*(x-0.976)*(x-0.977)*(x-0.978)*(x-0.979)*\
(x-0.980)*(x-0.981)*(x-0.982)*(x-0.983)*(x-0.984)*(x-0.985)*(x-0.986)*(x-0.987)*(x-0.988)*(x-0.989)*\
(x-0.990)*(x-0.991)*(x-0.992)*(x-0.993)*(x-0.994)*(x-0.995)*(x-0.996)*(x-0.997)*(x-0.998)*(x-0.999)*\
(x-1.000)*(x-1.001)*(x-1.002)*(x-1.003)*(x-1.004)*(x-1.005)*(x-1.006)*(x-1.007)*(x-1.008)*(x-1.009)*\
(x-1.010)*(x-1.011)*(x-1.012)*(x-1.013)*(x-1.014)*(x-1.015)*(x-1.016)*(x-1.017)*(x-1.018)*(x-1.019)*\
(x-1.020)*(x-1.021)*(x-1.022)*(x-1.023)*(x-1.024)*(x-1.025)*(x-1.026)*(x-1.027)*(x-1.028)*(x-1.029)*\
(x-1.030)*(x-1.031)*(x-1.032)*(x-1.033)*(x-1.034)*(x-1.035)*(x-1.036)*(x-1.037)*(x-1.038)*(x-1.039)*\
(x-1.040)*(x-1.041)*(x-1.042)*(x-1.043)*(x-1.044)*(x-1.045)*(x-1.046)*(x-1.047)*(x-1.048)*(x-1.049)
plt.plot([0.949,1.051],[0,0],C="Gray")
plt.plot(x, y,C="Red")
plt.ylim([-2e-171,2e-171])
plt.xlim([0.949,1.051])
plt.xlabel('x')
plt.ylabel('y')
plt.title("Zoom up y axis")
plt.show()
このように1.00近傍にだけ解を持つという特殊な代数方程式であれば、それが100次方程式であっても、Raspberry Pi のpythonプログラムで解くことができました。
最後までご覧いただき、ありがとうございました。
次回に予定していた重解ありの高次方程式は、残念ながらプログラムが作成できずとりやめになりました。また他のテーマを探してRaspberry Piのpythonでプログラムを作ってみようと思っています。
今回はQiitaの主旨に同意して投稿していますので、公開したプログラムはコピー、改変などでのご使用は自由です。著作権に関する問題も発生しません。
ただし、Raspberry Pi 4Bを使う場合にはCPUに特に大きめのヒートシンクが必須です。LAN通信の頻度の少ない今回のプログラムのような場合、LANチップは熱くなりません。しかし計算時間が継続するとCPUの激しい発熱で分かるように相当電力を使っています。電源USB Cタイプの後ろにある黒い小さなチップも熱くなりますので、ファンでの風流も必要です。