現在、Python・データ解析(統計含む)を勉強中なので、このページでは勉強しながら、統計とPythonでのグラフ化などについてメモを追加していく。
データに基づく判断はロジカルシンキングでは防げない判断の誤りを防ぐことができる力を持つ、有効なツールなので積極的に勉強していきたところ。
※注意※
勉強しながら記載しているので誤解して記述する可能性があります。気づき次第修正しますが、誤りに気付かれたときには、指摘いただけると幸いです。
参考図書
・栗原伸一著「入門 統計学」
・Wes McKinney著「Pythonによるデータ分析入門」
・あんちべ著「データ解析の実務プロセス入門」
・Bill Lubanovic著「入門Python3」
・藤井良宜ら著「日本統計学会公式認定 統計検定3級対応 データの分析」
・田中豊ら著「改訂版 日本統計学会公式認定 統計検定2級対応 統計学基礎」
・南風原著「心理統計学の基礎」
2冊統計検定のテキストが含まれていますが、テキストの内容というよりは、どちらかというと統計検定に向けて学習することがオススメです。民間資格ですが、なかなか良い問題を出してくる資格試験だと思います。ちなみに、統計検定3級は公式テキストだけでいけます。2級は、あんちべ氏推奨の栗原著「入門 統計学」が良いです。これだけで良いです。
要約統計量
標本平均(分散)、不偏平均(分散)
統計を学習するときに分散の計算で、標本数nで割ったり、n-1で割ったりするが、ここらへんをしっかり理解しないと混乱のもとになる。
記述統計の立場、つまり取ってきた標本を要約して統計値として特徴を示そうとするときには、標本平均・標本分散と表現して、標本数nで割る。
推測統計の立場としては、不偏性という望ましい性質、つまり、推定量の期待値が推定しようとしている母集団の真の値に一致する性質を持つ値を採用する。まず標本平均については、そのままで不偏性を持つことからこれを推測統計の立場においても採用する。推測統計の立場で分散を推測するときには、標本を取ってくるときの誤差を考えた結果であったり、標本分散が真の分散に比べて小さい値になる傾向を考慮して、標本数n-1で割ることになる。
(算術)平均と中央値
外れ値がある場合や、データに偏りがある場合には、中央値と思いがち(な気がするの)だが、平均値は、ある点から各データまでの「距離」の2乗値を最小にする統計量であり、中央値は、距離の絶対値(2乗ではない)を最小化する統計量。異なる基準を最適化する値なので、単純にどちらが適切か言えない。平均値と中央値が大きくことなる値をとるときには、両方の値を示すことが推奨される。
データの分布の形状から値が大きく異なってくるのであれば、ヒストグラムもあわせて提示するといいのかもしれませんね。
標準化変量と偏差値
(複数の)データx_iで、データから計算した(母集団の)平均μ、(母集団の)標準偏差σとしたときに、z_i=(x_i-μ)/ σ で計算する値が標準化変量です。
平均ゼロ、偏差1にしたいわけですね。統計検定3級や2級(および現実の問題)では、生徒Aの数学の成績と理科の成績を比較することがあります。しかし、科目によって平均点や分散が異なるわけです。そのままでは比較が難しいので、標準化変量を計算します。
標準化されているので、値の大小だけで異なる科目の成績を比較できるようになります。ちなみに、偏差値は、この標準化変量を10倍して、50を足した値になります。
y=ax+bで、データを変換したとき、平均値は、aE[x]+b、偏差は|a|倍になるので、偏差値というのは、標準化変量をつかって、平均値50点,偏差10点の値を作ったということになります。こう考えると、偏差値というものがどういうものか覚えやすいと思います。統計検定でも、暗記していることが前提になります。
変動係数
平均値が異なる分布の分散を比較するのは、難しいです。そこで、(偏差)/(平均)で計算するのが変動係数です。平均値の差を吸収して値のちらばりを比較しやすくします。統計検定3級でも出るくらいなので記憶が必要です。計算もシンプルなので実生活でも使えると思います。
変動係数、という単語だけ覚えると平均値が分母だったか分子だったか混乱してしまうこともあると思います。そこで、大前提として「変動係数は分散同様に、値のちらばりを考えるときの値である」ことを覚えておけば、偏差が分子、平均値が分母にくることが覚えやすいと思います。平均をゼロ、標準偏差を1に変換するときの標準化変量と混乱しないように注意が必要かと思います。
まず、xの平均がE[x]、分散がV[x]とすると、y=ax+bすると、
E[y]=aE[x]+b、V[y]=|a|^2 *E[x]
です。
この関係を使って、dataを2種類つくって、スケールが異なるものの、似たような分散のデータに対して、変動係数を計算して、似たような値になることを以下で試してみました。
※0.4程度の違いをどう評価したらよいのかは、現時点で私は理解できていません。
※標本サイズで割られているのか、-1されているのか、以下のソースで確認していないのですが、標本サイズがある程度大きいと差は無視できるとして、気にしないことにします。
import numpy as np
import matplotlib.pyplot as plt
def main():
sample_size = 1000
a = 10
b = 5
data = np.random.standard_normal(sample_size)+1
data2 = a*data+b
print('data Mean:{} Var:{}'.format(np.mean(data), np.var(data)))
print('data2 Mean:{} Var:{}'.format(np.mean(data2), np.var(data2)))
print('coefficient of var {} : {}'.format(np.std(data)/np.mean(data), np.std(data2)/np.mean(data2)))
plt.subplot(2, 1, 1)
plt.hist(data)
plt.subplot(2, 1, 2)
plt.hist(data2)
plt.show()
if __name__ == "__main__":
main()
y=ax+bでの確率変数の変換
平均μ,分散σ^2の確率変数xに、ax+bの変換をすると、平均がaμ+b,分散が|a|^2になる関係を利用すると、
N(0,1)に従う乱数を生成する、numpyのrandnをつかって、平均μ、分散σ^2の正規分布に従う乱数を生成したいときには、
σrandn() + μ
すればいいことがわかる。
numpyのサイト:http://docs.scipy.org/doc/numpy/reference/generated/numpy.random.randn.html
にも、書かれている。
歪度と尖度
統計分布の非対称性を表す値が、歪度(わいど)です。ゼロが左右対称を表し、正になるときには、上側にのびる分布になっていることを示します。負であればその反対です。scipyでも計算する関数がありますし、もちろんエクセルにもあります。
※scipy http://docs.scipy.org/doc/scipy-0.15.1/reference/generated/scipy.stats.skew.html
実用上は、外れ値の有無の確認に使える、ということです。例えば、大きく正の値があるときには、プラス方向に、大きな外れ値がある、ことを示します。外れ値は、統計データを要約するとき(ものによって影響の大きさは変わりますが)影響があるので、なんらかの形で処理する必要があります。その必要性を考えるときに使える値、ということになります。
人力で処理する場合には、ヒストグラムを描くなり、散布図を描くなりすれば、外れ値には気付くことができますが、プログラムで外れ値に応じて処理を変えたい場合などに、有用な気がしますね。
尖度は、正規分布と比較したときに、どれだけいま考えている分布がとんがっているのかを示す値です。KURTで計算ができます。
統計関連のソースをみていると、SKEWやKURTが出てきたりしますが、歪度と尖度を受けているわけです。
例えば、あんちべさんの本の、外れ値を含む、dirty_iris.csvのデータ(Googleで検索すると、Githubのページが出てきます)を読み込んで、統計量や歪度を以下のように計算してみます。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
def main():
iris = pd.read_csv('./dirty_iris.csv')
print(iris.head(n=5))
print(iris.describe())
print(iris.skew())
if __name__ == "__main__":
main()
sepallength sepalwidth petallength petalwidth class
0 5.1 3.5 1.4 0.2 setosa
1 4.9 3.0 1.4 0.2 setosa
2 4.7 3.2 1.3 0.2 setosa
3 4.6 3.1 1.5 0.2 setosa
4 5.0 3.6 1.4 0.2 setosa
sepallength sepalwidth petallength
count 150.000000 150.000000 150.000000
mean 6.464000 3.040667 3.738000
std 7.651181 0.578136 1.763221
min 4.300000 -1.000000 1.000000
25% 5.100000 2.800000 1.600000
50% 5.800000 3.000000 4.300000
75% 6.400000 3.300000 5.100000
max 99.000000 5.400000 6.900000
sepallength 12.030413
sepalwidth -1.681226
petallength -0.248723
dtype: float64
となりまして、describeだけでも、sepallengthがあやしいのはなんとなく気づけるのですが、skewで出た値でも、他にくらべて、sepallengthがあやしいのがわかるわけです。
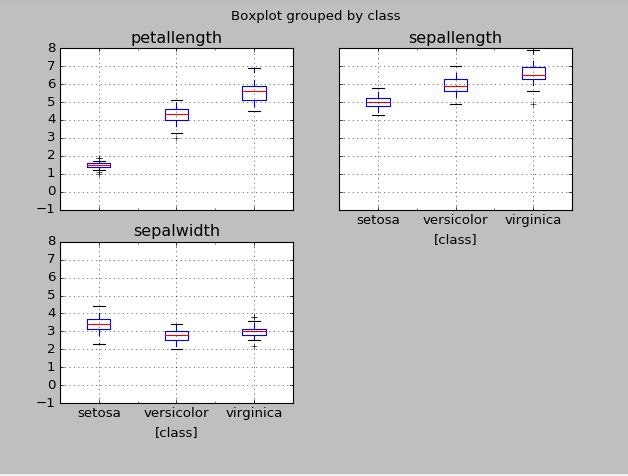
※上のデータで箱ひげ図を描いてみたところ、想像に反して外れ値の存在が見にくく(縦軸のスケールがおかしくて気づけるといえば気づけるのですが)、歪度skewの計算の有用性を実感しました。、
外れ値については、単に除外すればいいというものではなく、なぜその値がデータにあるのかを、ドメイン知識(業務知識や専門知識といった解析している分野の知識)を使って、対処方法を考える必要があるのですが、今回は適当にNaNとすることにして、
iris[np.abs(iris['sepallength'])>10] = np.nan
iris.boxplot(by='class')
plt.show()
すると、いい感じの箱ひげ図になりました。
※外れ値以外にも変な値はありまずが、とりあえず、歪度をつかって外れ値を見つける、ということで。
統計分布
ポアソン分布
ポアソン分布については、稀に起こる事象の解析に用いられる統計分布。
平均値=(分散=)λとするとき、
λ=(試行回数n) × (確率p)であることがポイントになる。pで起こる事象について、実際に起きる回数xを指定することで確率の値が得られる。
n,p,xは、問題の解釈次第で設定の仕方が異なることがあるが、ポアソン分布の式にしたときには、解釈がちがっていても、同じ数式になって同じ確率を計算できるので、心配しなくてよい。
実際に事が起きる回数xによって異なる値が得られるので、たとえば、k回以下である確率を求めるような場合には、複数回の計算を繰り返す必要がある。でもプログラムを使えば簡単だし、確率の和がある値になるときの回数も、scipyとか使えば計算できるので、あまり問題にならなさそう。
※ポアソン分布は平均値と分散が同じ値になる。分散の導出時には、V[x]=E[x^2]-E[x]^2の関係式を用いると楽になる。V[]は[]の中身の分散、E[]は[]の中身の期待値。
scipyだと参考になるのが、
http://docs.scipy.org/doc/scipy/reference/generated/scipy.stats.poisson.html
上のページで、細い縦棒でグラフを書く方法が興味深かったので引用して解説。
>>> ax.plot(x, poisson.pmf(x, mu), 'bo', ms=8, label='poisson pmf')
>>> ax.vlines(x, 0, poisson.pmf(x, mu), colors='b', lw=5, alpha=0.5)
まずは、'bo'で青丸で値を描画して、そのあと、ax.vlinesで、縦線を描画している。xが縦線の位置で、0が縦線の下端で、poisson.pmf(x,mu)で縦線の上端を指定してる。lwはline widthの略語だろう。alphaは線の透明度の指定。グラフを見やすくするときに横軸の範囲を指定するには、plt.xlim()を利用する。
ちなみに、pmfは、確率質量関数(Probability mass function)の略です。連続値の場合は確率密度関数(PDF)ですが、ポアソン分布のような離散値の場合は、PMFです。
可視化手法
箱ひげ図(boxplot)
探索的データ分析に重要な、データの可視化ですが、よく使われる散布図やヒストグラムに加えて、箱ひげ図も知っておくとよいと思います。統計3級でも必要な知識になります。複数のデータの分布を比較するのに適しています。
ヒストグラムを描いたときにわかる、山の数などの情報は消えてしまうのですが、これに対応した、ヴァイオリンプロット、というものもありますが、若干きもいデザインです。
※参考:http://stat.biopapyrus.net/graph/violinplot.html
外れ値の表現方法がちょっとポイントで、(第3四分位数)-(第1四分位数)の1.5倍以上、それぞれの値から離れた値を外れ値にすることが多いようです。扱うデータによって、外れ値の定義は変わるはずで、ここらへんは、デフォルトのままでよいわけではないところかと思います。
山が1つであれば、箱ひげ図の形から、だいたいヒストグラムを想像できるので、そういうデータが複数あるときの比較に、箱ひげ図は便利です。キモいヴァイオリンプロットでもいいですけどね。Pythonなら描けるし。