確率伝播法とは
確率伝播法とは信念伝播法(Belief Propagation)ともよばれ,ベイジアンネットワークやマルコフ確率場(MRF)などのグラフィカルモデル上で各ノードが持つ状態の周辺分布を効率的に求めるためのアルゴリズムです.元々はこの周辺分布を求めようとするとノード数がNで状態数がKとすると,計算量が$O(K^N)$となり,ノード数が多くなると有限時間で計算が出来なくなります.でもこの確率伝播法を使うと$O(NK^2)$となり有限時間で計算できるようになります.この周辺分布が求められると何が便利かというと,グラフの構造によっては各ノードの最適な状態が周辺分布を使って求められたり,最適解でなくともそれに近い解を求められることです.今回はPythonでこの確率伝播法を組んでみたので順を追ってそのコードの解説を行っていきたいと思います.
プログラム解説
使用データ
今回はノイズのかかったレナさんの画像に対して確率伝播法を適用し,ノイズ除去を行いたいと思います.各画素がとる値は0と1の2値です.
プログラム
まずは原画像に対してノイズを掛けます.コードは以下の様になります.
```python: def addNoise(image): output = np.copy(image) flags = np.random.binomial(n=1, p=0.05, size=image.shape)for i in range(image.shape[0]):
for j in range(image.shape[1]):
if flags[i,j]:
output[i,j] = not(output[i,j])
return output
<p>次に画像中の各画素をノードとみなし,MRFを構築します.このMRFクラスで特に注目すべきはbeliefPropagation関数です.画像上でのマルコフ確率場はループ構造をもったネットワークなのでメッセージ送信を複数回繰り返す必要があります.今回はそれをiter回繰り返します.送信を繰り返す前に各ノードが隣接するノードから受け取るメッセージを1で初期化しておきます.送信ループに入った後は隣接ノードへsendMessageメソッドでメッセージを送信し続け,最後に各ノードについて自分が持つ隣接ノードからのメッセージを統合し,周辺分布を計算します.これを行うのがmarginalメソッドです.</p>
```python:
class MRF:
def __init__(self):
self.nodes = [] #MRF上のノード
self.id = {} #ノードのID
#MRFにノードを追加する
def addNode(self, id, node):
self.nodes.append(node)
self.id[id] = node
#IDに応じたノードを返す
def getNode(self, id):
return self.id[id]
#全部のノードを返す
def getNodes(self):
return self.nodes
#確率伝播を開始する
def beliefPropagation(self, iter=20):
#各ノードについて隣接ノードからのメッセージを初期化
for node in self.nodes:
node.initializeMessage()
#一定回数繰り返す
for t in range(iter):
print(t)
#各ノードについて,そのノードに隣接するノードへメッセージを送信する
for node in self.nodes:
for neighbor in node.getNeighbor():
neighbor.message[node] = node.sendMessage(neighbor)
#各ノードについて周辺分布を計算する
for node in self.nodes:
node.marginal()
次にノードクラスを定義します.
```python: class Node(object): def __init__(self, id): self.id = id self.neighbor = [] self.message = {} self.prob = None #エネルギー関数用パラメータ
self.alpha = 10.0
self.beta = 5.0
def addNeighbor(self, node):
self.neighbor.append(node)
def getNeighbor(self):
return self.neighbor
#隣接ノードからのメッセージを初期化
def initializeMessage(self):
for neighbor in self.neighbor:
self.message[neighbor] = np.array([1.0, 1.0])
#全てのメッセージを統合
#probは周辺分布
def marginal(self):
prob = 1.0
for message in self.message.values():
prob *= message
prob /= np.sum(prob)
self.prob = prob
#隣接ノードの状態を考慮した尤度を計算
def sendMessage(self, target):
neighbor_message = 1.0
for neighbor in self.message.keys():
if neighbor != target:
neighbor_message *= self.message[neighbor]
compatibility_0 = np.array([np.exp(-self.beta * np.abs(0.0 - 0.0)), np.exp(-self.beta * np.abs(0.0 - 1.0))])
compatibility_1 = np.array([np.exp(-self.beta * np.abs(1.0 - 0.0)), np.exp(-self.beta * np.abs(1.0 - 1.0))])
message = np.array([np.sum(neighbor_message * compatibility_0), np.sum(neighbor_message * compatibility_1)])
message /= np.sum(message)
return message
#観測値から計算する尤度
def calcLikelihood(self, value):
likelihood = np.array([0.0, 0.0])
if value == 0:
likelihood[0] = np.exp(-self.alpha * 0.0)
likelihood[1] = np.exp(-self.alpha * 1.0)
else:
likelihood[0] = np.exp(-self.alpha * 1.0)
likelihood[1] = np.exp(-self.alpha * 0.0)
self.message[self] = likelihood
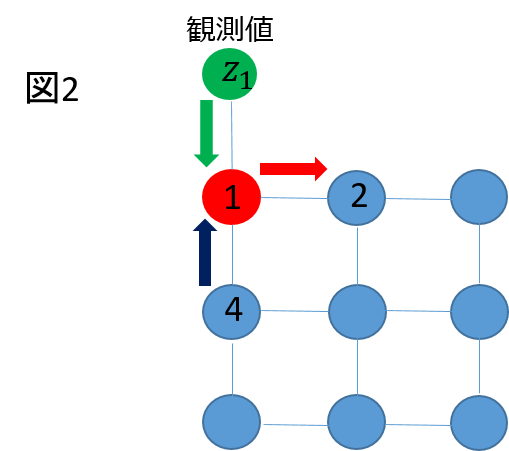
<p>重要なのはcalcLikelihood,sendMessage,marginalメソッドです.図1のようにノード1からノード2にメッセージを送信したいとします.このメッセージはノード1からノード2を見た時に,ノード2がどの値をとるべきかを教えるための物です.</p>

<p>それを計算するためにはまずノード1の各値についてその信頼度(その値をとった時の妥当性)を計算する必要があります.まずノード1の観測値のみを見た時の信頼度を計算します.これを計算しているのがcalcLikelihoodメソッドです.もし観測値が0ならノードが0をとるだろうという信頼度が高まり,逆にノードが1をとるだろうという信頼度が下がります.もし観測値が1をとればその逆になります.</p>
<p>次に観測値から計算された信頼度に,ノード4から見たときのノード1の各値の信頼度(ノード4からノード1へのメッセージ)を掛けてあげます.これらを表したのが図2です.この計算ではコード中ではsendMessageメソッド中の</p>
```python:
neighbor_message = 1.0
for neighbor in self.message.keys():
if neighbor != target:
neighbor_message *= self.message[neighbor]
の部分です.
そしてこれらを使ってノード2へ送信するメッセージを計算します.そのメッセージ(信頼度)は以下の様に計算されます.
これを計算しているのがsendMessageメソッド中の
```python: compatibility_0 = np.array([np.exp(-self.beta * np.abs(0.0 - 0.0)), np.exp(-self.beta * np.abs(0.0 - 1.0))]) compatibility_1 = np.array([np.exp(-self.beta * np.abs(1.0 - 0.0)), np.exp(-self.beta * np.abs(1.0 - 1.0))])message = np.array([np.sum(neighbor_message * compatibility_0), np.sum(neighbor_message * compatibility_1)])
message /= np.sum(message)
<p>になります.</p>
<p>これを全てのノードにおいて隣接するノードへメッセージ送信を行います.これを複数回繰り返した後,最後にmarginalメソッドでノードが隣接ノードからもらったメッセージを全て掛けることで周辺分布が求まり,ノードがどの値をとるべきかが分かります.</p>
<p>次はマルコフ確率場を構築するための関数を作成します.</p>
```python:
# 各画素ごとにノードを作成し,隣接画素ノードとの接続を作成する
def generateBeliefNetwork(image):
network = MRF()
height, width = image.shape
for i in range(height):
for j in range(width):
nodeID = width * i + j
node = Node(nodeID)
network.addNode(nodeID, node)
dy = [-1, 0, 0, 1]
dx = [0, -1, 1, 0]
for i in range(height):
for j in range(width):
node = network.getNode(width * i + j)
for k in range(4):
if i + dy[k] >= 0 and i + dy[k] < height and j + dx[k] >= 0 and j + dx[k] < width:
neighbor = network.getNode(width * (i + dy[k]) + j + dx[k])
node.addNeighbor(neighbor)
return network
最後はメイン関数です
import numpy as np
import cv2
import matplotlib.pyplot as plt
from skimage.filters import threshold_otsu
def main():
#使用データ
image = cv2.imread("Lenna.png", 0)
binary = image > threshold_otsu(image).astype(np.int)
noise = addNoise(binary)
#MRF構築
network = generateBeliefNetwork(image)
#観測値(画素値)から尤度を作成
for i in range(image.shape[0]):
for j in range(image.shape[1]):
node = network.getNode(image.shape[1] * i + j)
node.calcLikelihood(noise[i,j])
#確率伝播法を行う
network.beliefPropagation()
#周辺分布は[0の確率,1の確率]の順番
#もし1の確率が大きければoutputの画素値を1に変える
output = np.zeros(noise.shape)
for i in range(output.shape[0]):
for j in range(output.shape[1]):
node = network.getNode(output.shape[1] * i + j)
prob = node.prob
if prob[1] > prob[0]:
output[i,j] = 1
#結果表示
plt.gray()
plt.subplot(121)
plt.imshow(noise)
plt.subplot(122)
plt.imshow(output)
plt.show()
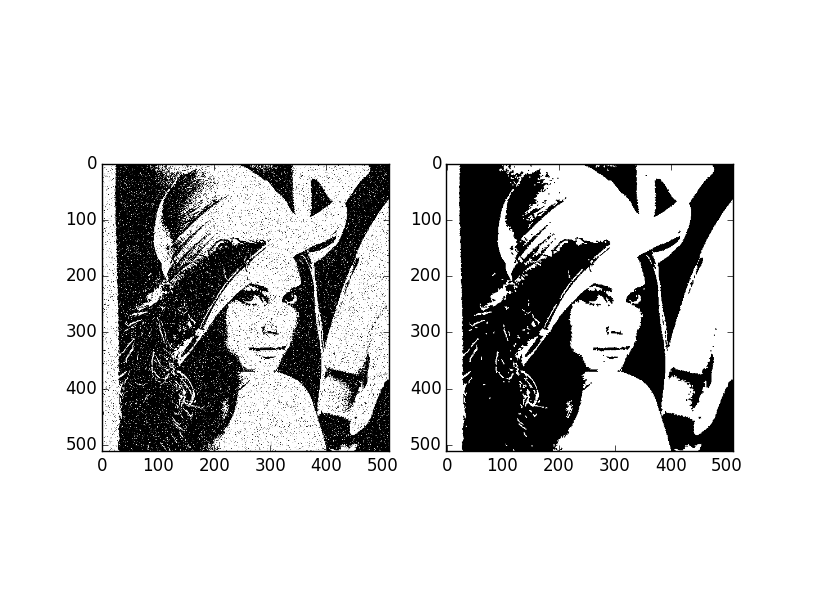
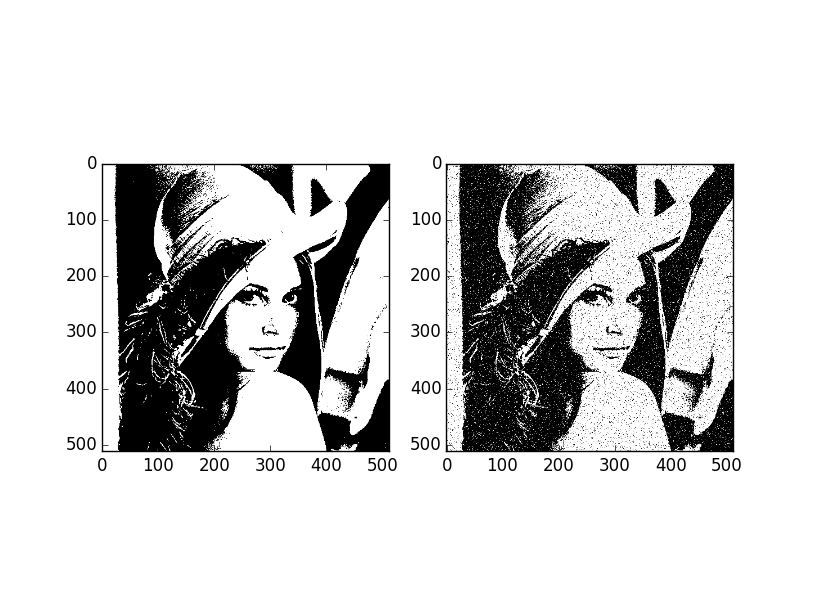
実行結果
確かに殆どのノイズが除去されて原画像が復元されていることが分かります.数式自体は結構難しいですが,プログラムで組んでみると結構簡単に組めます.今回は状態数が2値の離散的な場合を取り扱いましたが,トラッキングなどの連続的な状態を取り扱おうとすると連続変数版の確率伝播法を用いる必要があります.様々なものが提案されていますが,比較的簡単に組めるMean shift Belief Propagationを次回は組んでみたいと思います.
参考文献・サイト
Python networkx でマルコフ確率場 / 確率伝搬法を実装する
有名なグラフ理論用のライブラリnetworkXを用いて確率伝播法によるデノイジングを行っています.図を使ってアルゴリズムを解説してくれているので非常に分かりやすいです.
東北大学のとある研究室の先生が書いたpowerpointのようです.図と数式を用いて分かりやすく解説してくれています.