全てのプログラムが、そのCPUの最大性能を出せるわけではない。
実際にはデータ転送時間がネックとなり、プログラムごとで性能上限がある。
メモリ性能が10GB/sであれば一秒間に10GBしか送れないということであり、基本的にCPUはデータ転送時間より早く処理するからデータが来るまで待ち時間が発生する。
(また、VPSなどの仮想サーバなどでも、メモリ性能があまり良くないことが多くあるようである。3項目目にさくらVPSのルーフラインモデルを計測した結果があります。)
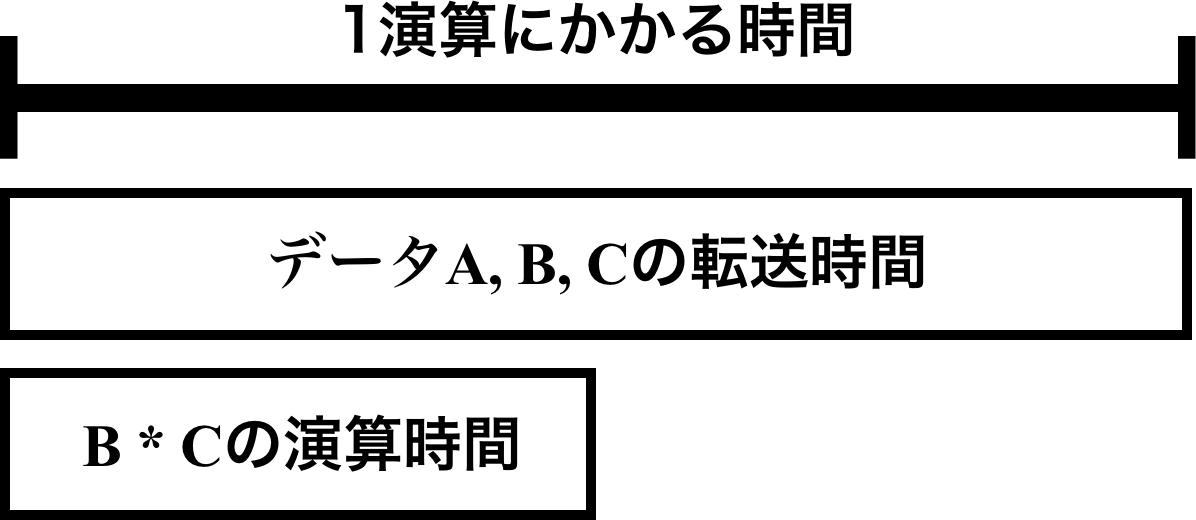
ルーフラインモデル
データ転送量によってプログラムの演算性能に上限があることを示したモデル。
途中で折れ曲がるため屋根のようであることからルーフラインモデルと呼ばれる。
「データ転送時間 < CPU内部の演算時間」となった瞬間にデータ転送時間のネックはなくなり、実測値の上限となる。
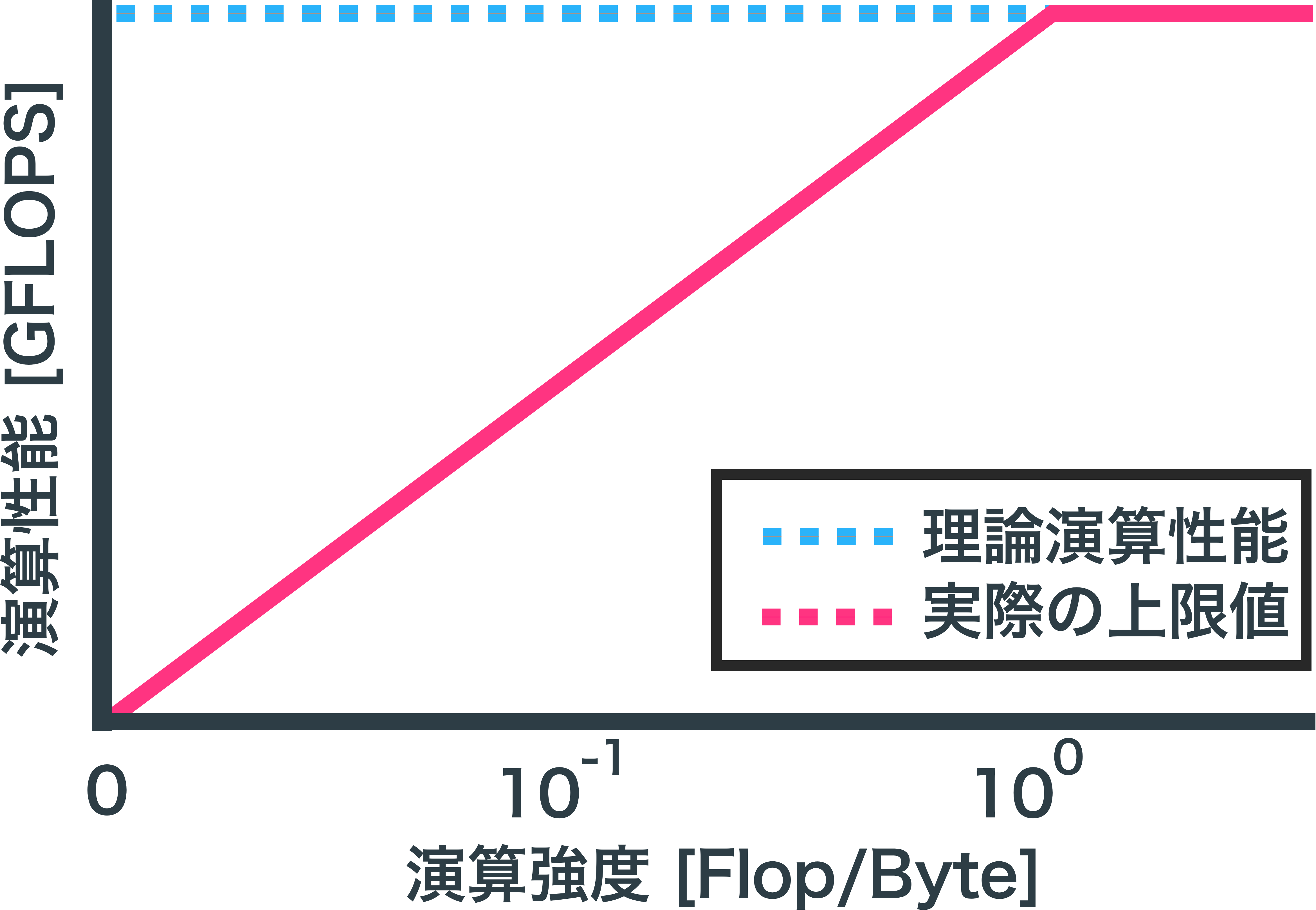
さくらVPS仮想3coreサーバでは
メモリ性能は予測上の最大値を考慮したが、実際にはもう少し低かったようである。
この図では、さくらVPS仮想3coreがメモリ性能が高くないことを示している。
左側のグラフはすぐにデータ転送時間のネックがなくなっているのに対して、右側のグラフはデータ転送時間のネックがなかなか無くなっていない。
このように半分ぐらい性能が変わったりもする。
右側のさくらVPSは最大値まで計測されてないがおそらく6GFlopsぐらいが上限値であると思われる。
青のグラフは最大値、緑のグラフは実測値である。
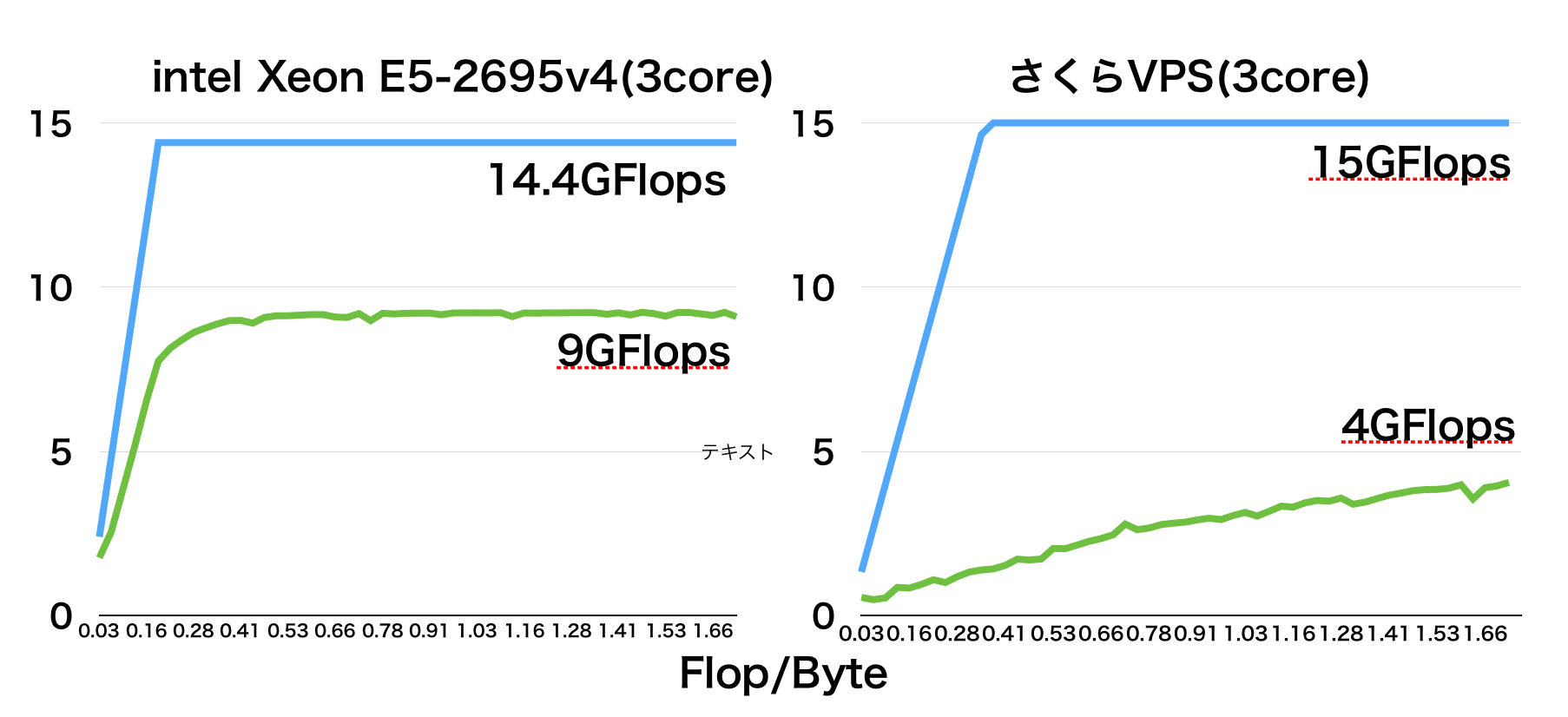
データ転送時間がネックになる
for(i=0;i<N;i++){
A=B*C;
}
という演算を例にする。
BとCを読み込んで、Aに書き込みをするという処理であり、3つのデータがCPUとメモリとの間を移動している。
一方、CPUの方での計算はB*C(mul命令)とデータを移動する(mov命令)の処理しかしていない。
ここでメモリ転送時間が演算時間よりも大きいと、データ転送が終わってから次のループが始まる。
以下の図で説明ができる。
これを計算式にすると、
以下の式が1反復ループあたりの演算時間となる。
MAX(データ転送時間, CPU内での演算時間)
このようにデータ転送時間がプログラムに大きな影響を与えている。
メモリを大量に読み込むプログラムの性能を上げるのであれば、DDR4などメモリの性能も考える必要がある。複数のCPUで処理を分散させるとメモリアクセスも分散されるためネックになりにくくなる。
演算強度とは
1Byteデータ転送あたりに何回浮動小数点演算をしているか(Flop/Byte)
Flop ÷ Byte
演算性能とは
一秒間に浮動小数点演算が何回できるか(GFlops)
Flop ÷ Time(Sec)
理論演算性能とは
そのシステムの最大の演算性能(GFLOPS)
・2.1GHz
・4コア
・加算器の数2つ
であった場合は、
2.1 × 4 × 2 = 16.8GFlops
がこのシステムの最大の演算性能である。(実際にはここまで性能はでない)
SIMDやMPIの処理を入れるとさらに大きくなる。
演算強度からの演算性能の求め方
・メモリバスの速度が16(GB/sec)
・演算強度が0.25
であった場合の最大性能は、
16 × 0.25 = 4GFlops
つまりメモリ性能が倍になると理論的な性能も倍になる。
演算強度の計測方法
演算強度はこのように設定できる。
※ 配列は全てdouble(8Byte)とする。
・FLOP=1, データ転送数 = 3, 演算強度 = 1Flop / (8Byte * 3) = 0.0416
for(i=0;i<N;i++){
A[i] = B[i] * C[i];
}
・FLOP=2, データ転送数 = 3, 演算強度 = 2Flop / (8Byte * 3) = 0.083
for(i=0;i<N;i++){
A[i] = B[i] * C[i] * C[i];
}
・FLOP=3, データ転送数 = 3, 演算強度 = 3Flop / (8Byte * 3) = 0.125
for(i=0;i<N;i++){
A[i] = B[i] * C[i] * C[i] * C[i];
}
配列Cが増えてもCPU内部のレジスタに保存されるため、データ転送数は3のままである。
*の数が増えれば、演算強度は増えていくことになる。
参考
ルーフラインモデル
https://www2.eecs.berkeley.edu/Pubs/TechRpts/2008/EECS-2008-134.pdf