はじめに
CodeIQで出題されていた「レッド・アンド・ホワイト」問題(by @riverplus さん)をRubyで解いてみました。
問題は次の通り。
マス目が横に直線状に並んでいます。
マス目は左右にどこまでも続いているものとします。
マス目はすべて白色で塗られています。
このうちの 1 つを赤色で塗ります。
以降、次のルールに従って、マス目の色を塗り替えていきます。
1 秒後、左右隣のマス目の色が白赤または赤白となるマス目を全て赤色で塗り、
そうでないマス目(つまり左右隣が白白または赤赤)を全て白色で塗ります。
以降、同様に、1 秒ごとに赤白でマス目を塗り替えていきます。
まずは解き方を説明する前に、提出したコードを示します。
p 2**gets.to_i.to_s(2).count('1')
コードの手順としては、
- 標準入力から自然数を読み込む
- それを数値化する
- それを二進数の文字列にする
- その中から1が何個あるか数える(個数をcとする)
- $2^c$が答えの数字
となります。
ようするに、関数$H(x)$を$x$の二進数と0とのハミング距離、$n$を標準入力に与えられた自然数とすると、**$2^{H(n)}$**が答えとなります。
これから、なぜこのように簡潔にコードを書けるか解説をしていきます。
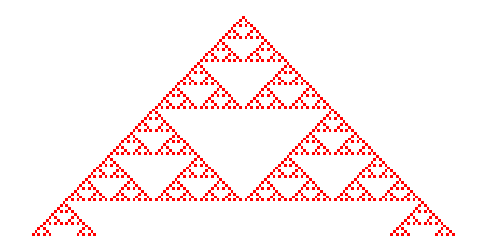
とりあえず、図示する
なんかどこかで見たことありません・・・?
そうです!これはシェルピンスキーのギャスケットです!
(複雑系の人とかはルール90の1次元セル・オートマトンとか呼んでるらしいです。)
そしてこれは、各行についてマス同士のすきまを詰めることで、
偶数マスを白、奇数マスを赤にしたパスカルの三角形と見ることもできます。
参考:「ずれたセルオートマトン・パスカルの三角形・フラクタル」 - roombaの日記
パスカルの三角形の上からn番目、左からk番目のマスは、二項係数${}_n \mathrm{C} _k$に対応しています。
また、${}_n \mathrm{C} _k$は、式$(1+x)^n$の展開式の項$x^k$の係数でもあります。
つまり、最終的に私たちは${}_n \mathrm{C} _k$の偶奇を確かめ、奇数の個数を数えれば良いことになります。
で、その偶奇とやらはどう確かめるの?
はい。${}_n \mathrm{C} _k,k=0~n$の偶奇を確かめれば簡単ですね!
・・・
これではnが増えたらトンデモないことになります。。。オーダーは$O(n^2)$ですからね
ここでは先ほど示した$(1+x)^n$の展開式の項$x^k$の係数の偶奇を確かめてみます。
そのためにまず、$n$の2進数の桁数をg、その$i$桁目数を$d_i$とすると、
n=\sum_{i=1}^{g} b_i, b_i = \begin{cases} 0 & (d_i=0) \\ 2^{i-1} & (d_i=1)\end{cases}
と表せることを利用し、
(1+x)^n=\prod_{i=1}^{g} (1+x)^{b_i}
と書き換えます。
ここで、私たちが興味があるのは,係数の偶奇についてなので、
係数の偶奇が同じ多項式を合同とみなすと(このことを「合同をとる」と呼ぶことにします)、
\begin{align}
c_i &= (1+x)^{b_i} \\
&\equiv \begin{cases}
1 & (b_i=0) \\
1+x & (b_i=1)
\end{cases}
\end{align}
より、
\begin{align}
(1+x)^n &= \prod_{i=1}^g (1+x)^{b_i} \\
&\equiv \prod_{i=1}^g c_i
\end{align}
と書けます。
このように変形していくことで、最終的に$(1+x)^n$の合同をとった多項式の項数を数えれば答えが導けることになります。
それでは、$\prod_{i=1}^g c_i$を乗算する際の計算し終わった多項式($F_i=\prod_{j=1}^{i} c_j$)の項数に注目してみます。
$F_i$の項数が増える要因は何なのでしょうか。$c_i$に何か秘密がありそうですよね。
実は、$c_i$をかけた際、$L_i$の項数は$2^{d_i}$倍(これは$c_i$の定義を見てみるとわかると思います)、
すなわち$d_i$が1である度に2倍になるのです。
ここまで書くと答えが見えてきますね。
そうです。まさに冒頭で述べた$H(n)$は、ちょうど**$\sum_{i=1}^{g} d_i$**となるのです。
よって、この問題の答えは、
\prod_{i=1}^g 2^{d_i} = 2^{\sum_{i=1}^{g} d_i} = 2^{H(n)}
となります。
これでオーダーは$O(\log n)$になりました!めでたしめでたし。
参考:2015年東大前期入試理系数学 大問5 - ほのぼの数学頑張ろう~
参考を見てもらえば分かりますが、
この問題は2015年東大前期入試理系数学 大問5と似た問題なのでした。おしまい
[おまけ] ちょっとゴルフやってみたい
出来心でコードゴルフをやってみました(笑)
p 2**("%b"%gets).count(?1) # Ruby(26)
もう少し縮められそうな気がしますが、気のせいってことにしておきます。