こんにちは、@cia_rana です!
これは CyberAgent 19新卒 エンジニア Advent Calendar 2018 の25日目の記事です。
はじめに
現在卒業研究として Delaunay triangulation (ドロネー三角形分割)のハードウェア実装による高速化を行っており、そこではベースのアルゴリズムに Fortune's Algorithm を使用しています(アルゴリズムの詳しい説明はしませんがリンク先のアニメーションが気持ちいいのでぜひご覧くださいw)。
ハードウェア実装をする際には、その前に実装するアルゴリズムが正しく動作するかどうか確認するためにデバッグの容易なソフトウェア実装を行うことが一般的です。Delaunay triangulation は(私の知る限りでは)計算幾何学的アルゴリズムを用いて行うため、可視化したほうがよりアルゴリズムの正しさを理解できると思い、ソフトウェア実装に加えて Go言語の2Dレンダリングライブラリの中で恐らく一番使われている github.com/fogleman/gg を用いて Fortune's Algorithm の計算過程を可視化しました。今回はその中でも Fortune's Algorithm のキモである放物線を描画する際に工夫した点に焦点を当ててお話します。
gg で Fortune's Algorithm 中の放物線を描画する上での注意点
gg で Fortune's Algorithm 中の放物線を描画する上でいくつか注意することがあります。
ひとつは gg には曲線描画関数にベジェ曲線しかなく(というと少し語弊がありますが...)、放物線を描画するために少々工夫が必要なことです。のちほど説明しますが、実は二次のベジェ曲線は放物線の一部であり、第1制御点と第3制御点は放物線上の点、第2制御点は第1制御点と第3制御点それぞれの接線の交点であるため、描画したい放物線の関数から開始点と終了点の$x$座標を指定してあげれば、ちょっとした計算により二次のベジェ曲線の制御点を求め放物線を描画できます。
ふたつ目に Fortune's Algorithm の放物線は、その性質からみなさんが中学・高校で習った $y=ax^2+bx+c$ の係数を直接与えて描画するのではなく、高校数学Ⅲあたりで習う焦点と準線からなる軌跡によって描画するため(しかも教科書に載っているそれは原点を通る前提なので、一般化する必要があります)、これもまたひと工夫する必要があります。
焦点と準線からなる放物線をベジェ曲線を使って描く流れ
上記の注意点をまとめると、
- 焦点と準線から放物線の関数を求める
- 放物線の関数からベジェ曲線の制御点を求める
- 制御点からベジェ曲線により放物線を描画する
の順で放物線を描画できることが分かります。それでは順に説明していきます。
焦点と準線から放物線の関数を求める
まずは高校数学Ⅲで習った焦点と準線と放物線の関係を復習します。
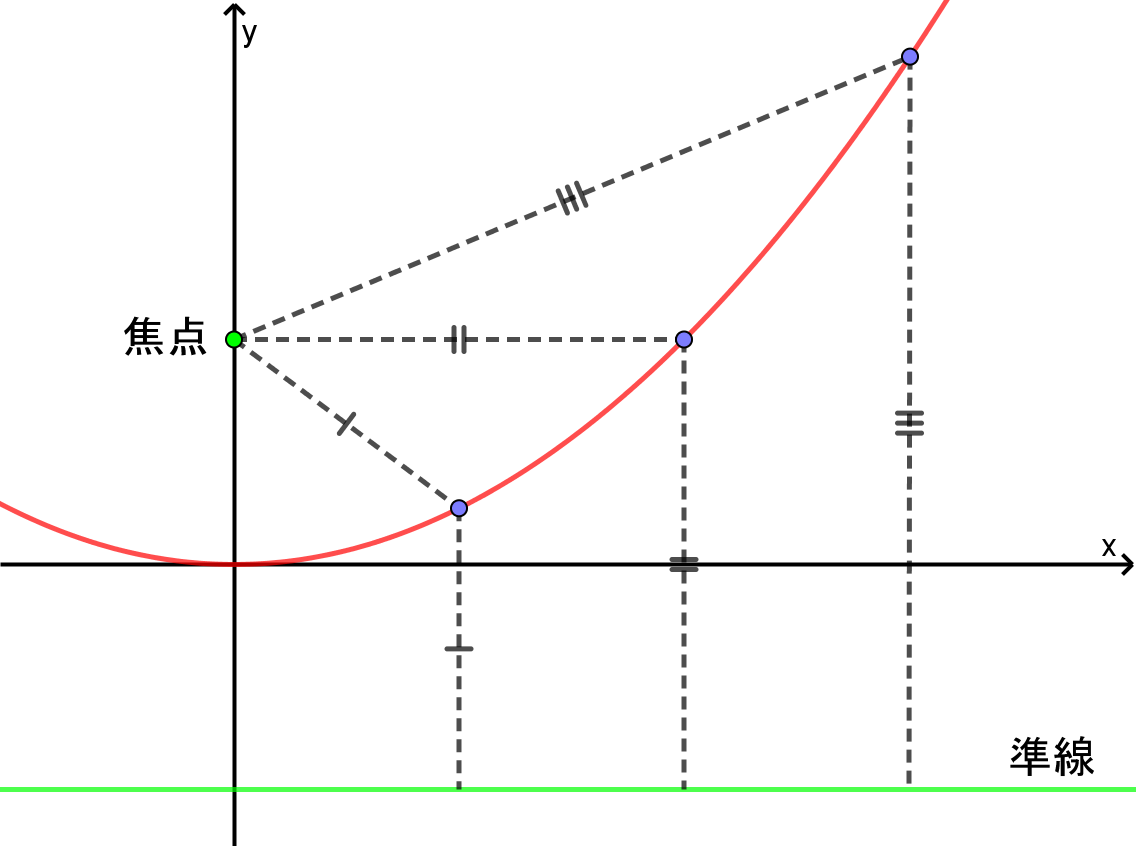
焦点と準線の意味を言葉で説明するのは難しいですが、以下の図を見ると焦点は文字通り平面上の点、準線も文字通り平面上の直線のことです。ここでは仮に教科書通り焦点の座標を $(0,\ p)$、準線の方程式を $y=-p$ とします($p $ は正数)。
それに対し放物線は、焦点からと準線からの距離が等しい平面上の点の軌跡です。
つまり、平面上の点 $(x, y)$ と焦点との距離は $\sqrt{x^2 + (y-p)^2}$、準線との距離は $|y+p|$ なので、放物線の方程式は、
\begin{eqnarray}
(y+p)^2 &=& x^2 + (y-p)^2 \Leftrightarrow y &=& \frac{1}{4p}x^2
\end{eqnarray}
となります。
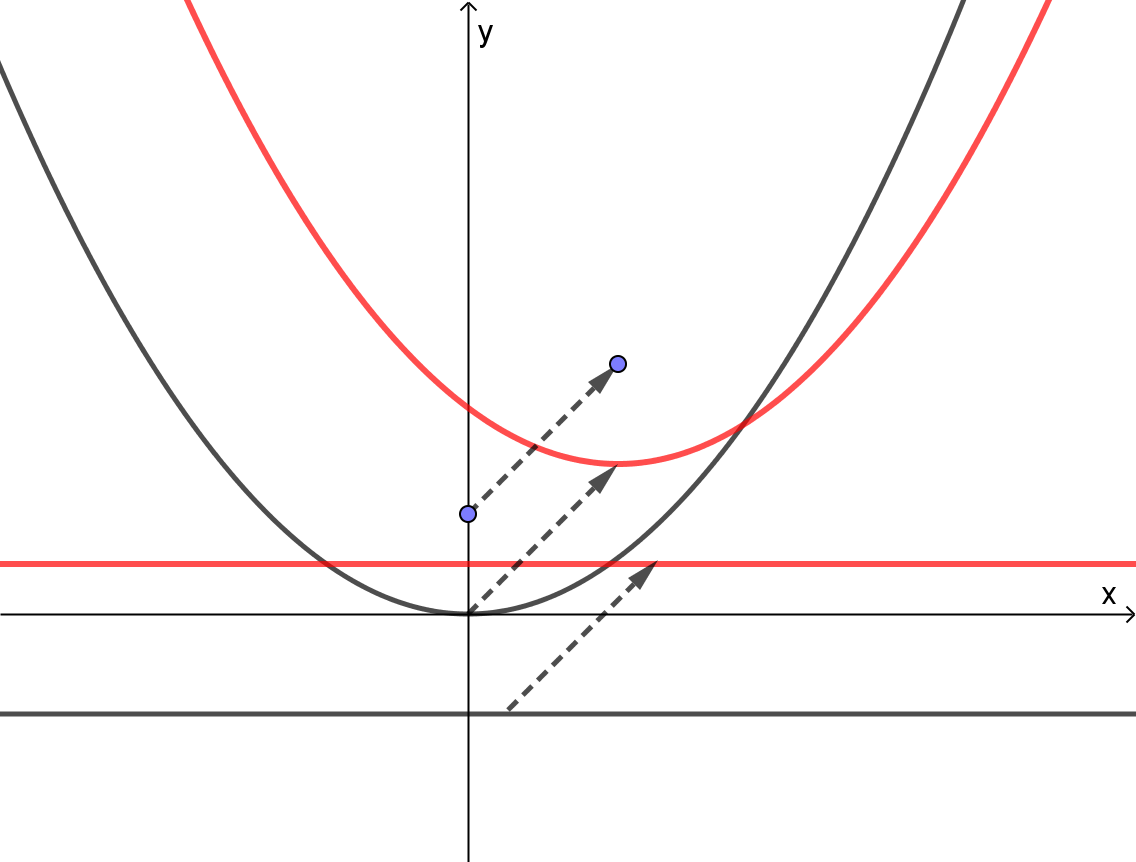
しかし、これは原点を通る放物線の方程式であり、Fortune's Algorithm に出てくる放物線は必ずしも原点を通るとは限りません。そこで以下の図のように原点を通る放物線をなす焦点と準線が与えられた焦点と準線に平行移動したと考えると、一般的な放物線も定義することができます。
与えられた焦点を $(s,\ t)$、準線を $y=q$ とすると、平行移動量は $(s, \ \frac{t+q}{2})$ であるため、放物線の方程式は、
y-\frac{t+q}{2}=\frac{1}{4 \cdot \frac{t-q}{2}}(x-s)^2 \\
y=\frac{1}{2(t-q)}x^2-\frac{s}{t-q}x+\frac{s^2+t^2-q^2}{2(t-q)}
となり、すなわち放物線の関数 $f$ は
f(x)=\frac{1}{2(t-q)}x^2-\frac{s}{t-q}x+\frac{s^2+t^2-q^2}{2(t-q)}
となります。
放物線の関数からベジェ曲線の制御点を求める
ベジェ曲線をご存じない方にも説明すると、ベジェ曲線とは $N$ 個の制御点から得られる $N-1$ 次曲線のことです。コンピュータ上で滑らかな曲線を描くときによく利用され、Google や Twitter のロゴがベジェ曲線で緻密に描かれていたり、パワポを使ってベジェ曲線でイラストを描いているのをネット上で見かけた方も多いでしょう。
具体的には制御点を $\boldsymbol{B_{0}},\ \boldsymbol{B_{1}},\ ...,\ \boldsymbol{B_{N-1}}$ とすると、ベジェ曲線 $P$ は
P(t)=\sum_{i=0}^{N-1}\boldsymbol{B}_{i}J_{N-1,\ i}(t)
と定義されます。なお、一般的には $0 \leq t \leq 1$ であり、この時 $\boldsymbol{B_{0}}$ と $\boldsymbol{B_{N-1}}$ を両端とするベジェ曲線が得られます。また、$J_{n,\ i}$ はバーンスタイン基底関数で以下で定義されます。
J_{n,\ i}(t)={}_{n}C_{i} t^i(1-t)^{n-i}.
一見複雑そうな数式ですが、二次のベジェ曲線の場合 $N=3$ なので
\begin{eqnarray}
&&\sum_{i=0}^{2}\boldsymbol{B}_{i}J_{2,\ i}(t) \\
&=&\boldsymbol{B_{0}}{}_{2}C_{0}t^0(1-t)^{2} + \boldsymbol{B_{1}}{}_{2}C_{1}t^1(1-t)^{1} + \boldsymbol{B_{2}}{}_{2}C_{2}t^2(1-t)^{0} \\
&=&\boldsymbol{B_{0}} \cdot 1 \cdot 1 \cdot (1-t)^2 + \boldsymbol{B_{1}} \cdot 2 \cdot t \cdot (1-t) + \boldsymbol{B_{2}} \cdot 1 \cdot t^2 \cdot 1 \\
&=&\boldsymbol{B_{0}}(1-t)^2 + \boldsymbol{B_{1}}2t(1-t) + \boldsymbol{B_{2}}t^2 \\
&=&(\boldsymbol{B_{0}}-2\boldsymbol{B_{1}}+\boldsymbol{B_{2}})t^2 + (-2\boldsymbol{B_{0}}+2\boldsymbol{B_{1}})t + \boldsymbol{B_{0}} \\
\end{eqnarray}
とシンプルな形式になり、二次のベジェ曲線は放物線でもあることが分かります(証明は省きますが双曲線や楕円にはなりえません。直線にはなりえます)。
次に二次のベジェ曲線の制御点を求めます。上述した通り第1,第3制御点はベジェ曲線の端点であり放物線上の点でもあるので、これらの制御点の座標をそれぞれ $\boldsymbol{B_{0}}=(x_0,\ ax_0^2+bx_0+c),\ \boldsymbol{B_{2}}=(x_2,\ ax_2^2+bx_2+c)$ と定めます。ただしこの放物線は焦点と準線から求めるので、
a=\frac{1}{2(t-q)},\ b=\frac{s}{t-q},\ c=\frac{s^2+t^2-q^2}{2(t-q)}
です。
第2制御点は上述した通り放物線上の第1制御点の接線と第3制御点の接線の交点になっているので、この交点を求めていきましょう。
一般的な放物線 $y=ax^2+bx+c$ 上の点 $(t,\ at^2+bt+c)$ における接線は $y'=2ax+b$ より $y=(2at+b)(x-t)+(at^2+bt+c)$ です。よって二接線の交点の座標は $\left(\frac{x_0+x_2}{2},\ ax_0x_2+\frac{b}{2}(x_0+x_2)+c\right)$ となり、これは同時に第2制御点 $\boldsymbol{B_1}$ でもあります。
制御点からベジェ曲線により放物線を描画する
ここまで放物線の関数やベジェ曲線の制御点を求めてきました。それでは具体的にライブラリ gg を使って放物線を描画していきましょう。
gg の二次のベジェ曲線を描画する(正確にはベジェ曲線上の離散的な点を求める)関数 gg.QuadraticBezier は第1から第3制御点の座標を引数にとるので、プログラムは次の通りになります。
var s, t float64 // 焦点の x, y 座標
var q float64 // 準線の y 座標
var x0, x2 float64 // 放物線の開始・終了位置の x 座標
tq := 1 / (t - q)
a := 0.5 * tq
b := -s * tq
c := (s*s + t*t - q*q) * 0.5 * tq
b0x := x0 // 第1制御点の x 座標
b0y := a*x0*x0 + b*x0 + c // 第1制御点の y 座標
b2x := x2 // 第3制御点の x 座標
b2y := a*x2*x2 + b*x2 + c // 第3制御点の y 座標
b1x := (x0 + x2) * 0.5 // 第2制御点の x 座標
b1y := a*x0*x2 + 0.5*b*(x0+x2) + c // 第2制御点の y 座標
points := gg.QuadraticBezier(b0x, b0y, b1x, b1y, b2x, b2y) // 放物線上の点群
おわりに
今回は焦点と準線からなる放物線を二次のベジェ曲線で描画する手順について説明してきました。放物線を描画するだけであれば素直に $y=ax^2+bx+c$ の $x$ の値を適宜変えて放物線上の点をサンプリングした後繋げばよいのですが、ベジェ曲線という多くのグラフィクスライブラリが備えている関数を利用することで、より手軽に放物線が描画できるのではないでしょうか。