2022/12/20 追記
本学内マップを実装した大元のWebサイトについての記事を、@いなにわうどんが筑波大学学園祭 Web サイト構築の舞台裏として執筆してくれました。ぜひそちらも併せてお読みください!
自己紹介
こんにちは。筑波大学情報メディア創成学類2年の@chururiです!
2022年度の筑波大学学園祭「雙峰祭」で、情報メディアシステム局(jsys)Web担当をしておりました。
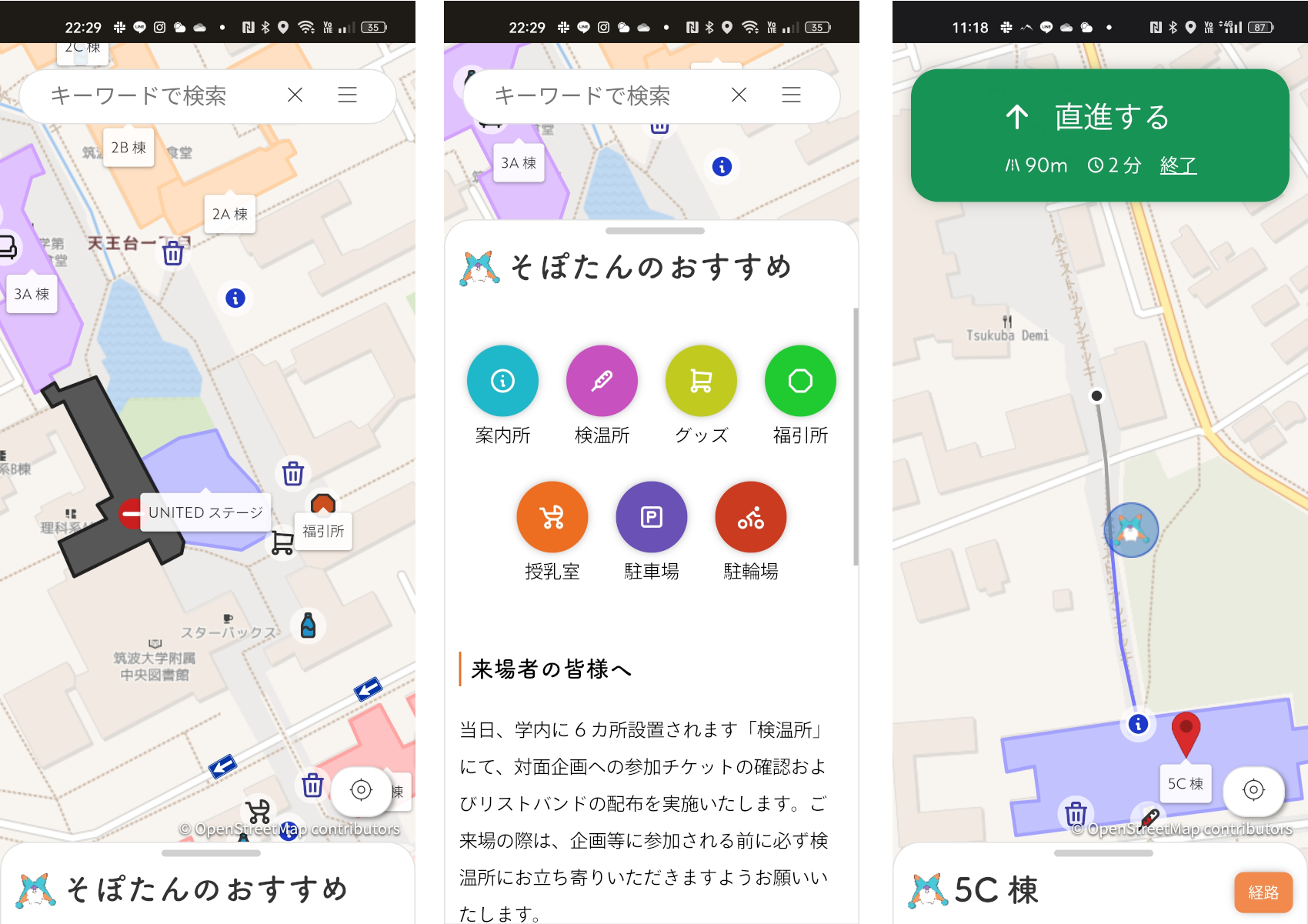
今回はその仕事の一つとして来場者向け学内マップを実装したので、それについて紹介したいと思います!
背景
「雙峰祭(そうほうさい)」は、筑波大学で毎年行われている学園祭です。第48回を飾る今年度の雙峰祭は、3年ぶりに来場者数制限をしたうえでの対面での実施となりました。そのため、来場者の多く(特に学外者)は筑波大学の敷地については慣れておらず、遭難者が発生してもおかしくない状況でした。
実際に3年前の19年度にも、遭難者を救おうとした勇者が現れています。今年は自分がその勇者になるべく、実装を決定しました。
いずれにせよ、筑波大学は大きすぎることで知られています。こことか見るとわかりやすいかもしれません。こんなの遭難者が出るに決まってます。
実装されている主な機能
- 各施設への経路表示と案内
- 各施設の位置表示
- 現在地情報と連携した近くの施設のサジェスト表示
- 施設等による企画検索
実際に↓のページから試すことができます!(実際に学内に行って試してみると面白いかもしれません!)
https://sohosai.com/maps 2022/12/1 公開終了しました
技術スタック
このマップを実装するにあたって、主に以下のライブラリや技術を用いています。
- next.js(フレームワーク)
- React Leaflet(マップコンポーネント)
- OpenStreetMap(マッププロバイダ)
- Vercel(ホスティング)
経路探索
ダイクストラ法
今回のマップにおいて、いちばん力を入れて実装したのが経路探索です。この経路探索はフロントエンドのみで実装しており、現在地をサーバー等に送信することなく実現しています。この経路探索はダイクストラ法を用いて実装されています。特に雙峰祭で使うマップでは、いくつか要件があります。
- 立ち入り禁止エリアがある
- Webの特性上、なるべく軽量かつ高速に動作させる必要がある
- データ通信量の削減
これらのことから、ダイクストラ法で使用する無向グラフのエッジを手作業でJSONに定義していくことにしました。OSMを使うエッジを抽出するツールを使ってもよかったのですが、
- エッジが極端に増えてしまうこと
- 立ち入り禁止に対応できない
などの理由から使用を見送りました。この選択により学内に約250個のエッジを設置するだけで済みました。また、コストにはエッジ間の距離を使用しています。予め計算しておいてもよかった(面倒くさかった)のですが、これについては計算の途中で随時計算することにしました(参考)。
データ構造
無向グラフのデータ構造には隣接リストを用いています。これはJSONで簡単に表現でき、かつグラフ構造が比較的疎であるためこの構造を選びました(これに対する実装方法として隣接行列を用いるものがあります)。実際にこのマップでは以下のように無向グラフとエッジを保存しています。
// キーはエッジID、値は緯度経度の配列
{
"1": [36.0000, 143.0000],
"2": [36.0001, 143.0001],
...
}
// キーは着目するエッジ、値は接続しているエッジのID
{
"1": [2],
"2": [1, 3],
...
}
また、計算を高速にするためにと優先度付きキュー(Priority Queue)を用いてダイクストラ法を実装しています。一般的なダイクストラ法の実装では計算量が$O(n^2)$となるのに対し、優先度付きキューでは$O((e+n)logn)$に抑えることができます。これにより、0.5秒以内での経路探索が可能となっています。
経路案内
マップのもう一つの機能として経路案内があります。これは、現在ルートのどの位置にいるかを判別し、次にすべき行動(右斜め前に曲がる、直進する...の後ろを除く7方向)を表示するものです。この経路案内はベクトルの内積計算によって実現しています。
例えば上のような状況があったとします。Aが現在地、Bが交差点、Cが次に進むべきエッジです。
このとき、$BA=\textbf{a}, BC=\textbf{b}$とすると、$\textbf{a}$と$\textbf{b}$のなす角$\theta$は$\theta=arccos(\textbf{a} \cdot \textbf{b}/|\textbf{a}||\textbf{b}|)$となります。しかし、この$\theta$の範囲は$0 \leq \theta \leq 180$なので、これでは右折なのか左折なのかわかりません。そのため、この範囲を$0 \leq \theta \lt 360$に補正する必要があります。
ここで登場するのがベクトルの外積です。外積には「右ねじの法則」というものがあり、なす角$\theta$が左回りならば外積のZ成分は0以上、右回りならば0以下になるという性質があります。従って、これを用いればなす角$\theta$を$0 \leq \theta \lt 360$に補正することができるというわけです。
結局、なす角$\theta$は$\theta = 360 - arccos(\textbf{a} \cdot \textbf{b}/|\textbf{a}||\textbf{b}|)\ (if\ \textbf{a} \times \textbf{b} \geq 0), otherwise\ arccos(\textbf{a} \cdot \textbf{b}/|\textbf{a}||\textbf{b}|)$と表すことができます。この情報をもとに、次にすべき行動を提案することができます(参考)。
コードで書くと以下のようになります(座標はマップの範囲が筑波大学であるという性質上、緯度と経度で近似しています)。
const A = [緯度, 経度];
const B = [緯度, 経度];
const C = [緯度, 経度];
const a = [B[0] - A[0], B[1] - A[1]];
const b = [B[0] - A[0], C[1] - C[1]];
const innerProduct = a[0] * b[0] + a[1] * b[1]; // 内積
const cos = innerProduct / getDistance(a) * getDistance(b); // cosθ
const outerZ = a[0] * b[1] - a[1] * b[0]; // 外積Z成分
let deg = (180 * Math.acos(cos)) / Math.PI; // 求める角度(degree)
deg = outerZ > 0 ? 360 - deg : deg; // 外積のZ成分が0以上なら左回り、そうでないなら右回り
おわりに
途方もない数のアクセスを受けるWeb開発は今回が初めてで、マップの実装が決まったときに正直自分にできるのか不安でした。しかし、jsysのWeb担当の他の2人のサポートもあり、協力して成し遂げることができました。めちゃくちゃ感謝しています。ありがとう。
関連リンク
- 筑波大学学園祭 Web サイト構築の舞台裏(2022年度)
- 遭難者を救うために学内Mapを作った話(2019年度)
- 約400企画が出店する学園祭を支えるWebサービスを開発した話(2018年度)
- 学園祭Webサイト制作(2018年度)