ペットボトルの底のあの形状を生成する

誰しも必ず見たことがある、炭酸飲料のペットボトルの底の、あの5角形のやつ、あれをプログラミングで作ってみようと考えました。

結論から言うと、だいたい自己評価で70点くらいの出来の形状ができました。結果が気になる方は先に一番下までスクロールして完成画像を見てから、この先を読むかどうか判断してください。

炭酸飲料のペットボトルの底の形

この5角形のやつです。

この形状は一般的にペタロイドと呼ばれています。「花の形に似たもの(petal-oid)」という意味です。下から覗いたときに花弁のように見えることでそう呼ばれています。

ご自宅に炭酸のペットボトルがあれば、一度底を眺めてみてください。

なぜこの形なの？

ペットボトルにはいろいろな形がありますが、この底部形状をとっているのは基本的に炭酸飲料だけです。炭酸飲料は内部からの圧力が強いので、お茶のボトルのような形状だと底が膨らんでしまいます。そのまま転がったり破裂したりと不具合が生じるので、強度を保つためにペタロイドが用いられているという話です。

実際にお茶のペットボトルに重曹を入れて強度を試してみる実験がありましたので、ご紹介しておきます。

ペットボトルの形には、深い秘密がある - ダイヤモンド・オンライン

ペタロイドを描く

目標

この記事の目標はペタロイドの形状をプログラミングにより生成することです。クオリティはそれなりを目指します(私のそれなりは世間一般よりユルユル判定なので、あまり期待しないでください)。

ググって資料を探す

なんかこう、簡単に数式1つで表現できたりしないかなぁと、いろいろ検索してみたのですが、なんの成果も得られませんでした。圧力試験のデータとかは出てくるのだけれども……。

多分CADとかで設計しているのかなぁ。

観察する

ネットに頼れないのであれば、自分でなんとかするしかありませんね。幸いにも実物はいくらでも手元にありますからね。まずはカッターを使って、ペットボトルの底の部分だけを切り出します。

さらに、ど真ん中から縦に真っ二つにしてみます。上の画像の12時方向から6時方向にバッサリとね。

分かったこと

• 円周上に同じ形が5つ並んでいる
• 谷の部分と山の部分が交互に存在する
• 谷の部分は中心から滑らかな曲線になっている
• 中心部は特に素材が厚い

まず、パッと見て分かりますが、同じ形が5個円周上に並んでいるので、そのうち1つを再現できれば、5個コピーして並べるだけで目標達成できることが分かります。

また、形状としては、交互に山と谷があり、谷の部分はおおよそ6～7mmの幅で中心から外周に向かって平行に筋が走っているように見えます。山の形状は大分複雑ですが、真上(あるいは真下)から見ると扇状、横から見ると台形のような形をしています。正確には山と谷の間は滑らかな曲線で傾斜が作られています。

断面図をみると、谷の部分の断面は楕円形の曲線を4分の1切り取ったようなスマートな曲線をしています。一方、山の部分の断面はちょっと複雑です。

あと、これはあまり記事に関係ありませんが、底の部分はかなり分厚くて、およそ3mmもありました。最初ハサミで切れるかと思っていましたが、刃が歯が立たなかったので、糸ノコを使う羽目になりました。

方針を定める

この情報から、どのように形状を再現するかを考えます。

まず、基本方針として、ボトルの中心を基準にものを考えることにします。
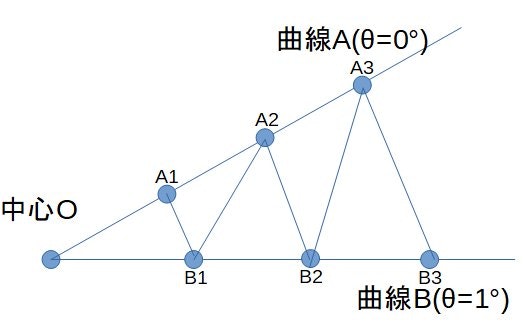
具体的には下の図のように、中心を基準として、方位角θの方向の断面形状を都度算出し、集積することで立体を再現しようと思います。

次に断面の形状の再現ですが、以下の3種類の異なる曲線を生成する必要があります。

• 谷の部分の楕円形の円弧
• 山の部分の複雑な曲線
• 傾斜の部分の複雑な曲線

もしかすると、一つの数式でまとめることもできるかもしれませんが、私の頭では思いつかないので、今回はスプライン曲線を使う方向で行くことにしました(困った時のスプライン)。

スプラインによる曲線の再現

前述の通り3種類の異なる曲線を、方位角$θ$という変数1つに基づいて生成する方法について考えます。

まず、谷の部分の曲線をスプライン関数で表すことを考えます。観察したとおりに、この曲線はおおよそ楕円上の円弧の形をしているので、スプラインで表すのは難しくありません。

簡便のため、以降では楕円ではなく、真円として表すことにします。楕円に戻したい場合は縦方向に拡大・縮小すればいいので。

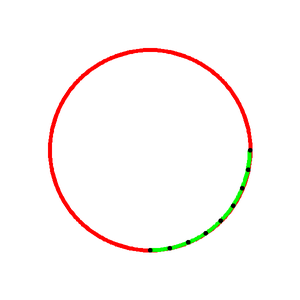
上図のように、円を描きます。第4象限(右下)部分の円弧上に$N$個の制御点を等間隔に配置し、これらをつなぐ3次スプライン曲線を描画します。この曲線は全ての制御点を通るように作られます。完璧に円弧に一致するわけではありませんが、人間の目では見分けがつかない曲線ですね。なお、$N=9$としています。

次は山の部分の曲線を作っていきます。ここでは、先ほどの谷の曲線を加工して、おおまかに観察した通りの山の曲線を模倣してみます。

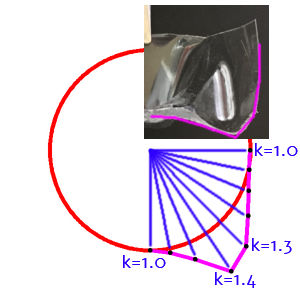
具体的に言うと、円弧上の制御点$(x_i,y_i)$を円の中心$(0,0)$から$k_i$倍して延長します($1 \leq i \leq N$)。以下の図のような感じで、ざっくり概形を作ります。

x'_i = x_i * k_i \\
y'_i = y_i * k_i

撮影した画像とにらめっこしながら、大体同じような形になるように$k_i$の値を微調整していきます。最終的なパラメータは

\begin{align}
K &= [k_1, k_2, k_3, ... , k_9]  \\
&= [1.00, 1.05, 1.18, 1.46, 1.36, 1.18, 1.07, 1.01, 1.00]
\end{align}

としました。端の点(k1とk9)は1.0にしないと出来上がりがおかしくなります。

制御点の数$N$の数を多くして、より正確な曲線を再現するようにすればクオリティが上がるかもしれませんが、調整がかなり大変です。完成した後で考えると、底の部分(左から4点目)の精度を高めるために、もう1,2点追加した方が良かったかも。

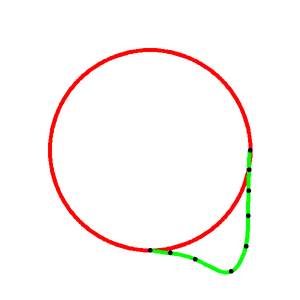
この概形をスプライン補間すると以下のようになります。実物のペットボトルを真横から見ながら$k_i$を調整したので、そこそこ似てる感じ。

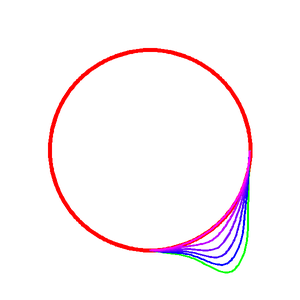
最後に、山と谷の間の傾斜部分の曲線を作ります。これは、山の曲線と谷の曲線を変形比率$D$という変数によってブレンドして求めます(やってることはただの線形補間)。

\begin{align}
x''_i &= x_i * D + x'_i * (1-D) \\
&= x_i * (D + k_i - Dk_i) \\
y''_i &= y_i * D + y'_i * (1-D) \\
&= y_i * (D+k_i - Dk_i)
\end{align}
\quad (0 \leq D \leq 1)

上の画像はDを0.0から1.0まで0.2刻みで傾斜部の曲線を描いたものです。D=0が赤紫、D=1が黄緑の線です。等高線のような、滑らかに山と谷を間を補う曲線を作れています。

方位角θと変形比率Dの関係

方針を決める際に、複数の方位角$θ$について、それぞれ断面の曲線を作ることにしました。また、曲線を作るために変形比率$D$という変数を導入したので、$θ$の値を元にして、$D$の値を求める必要があります。

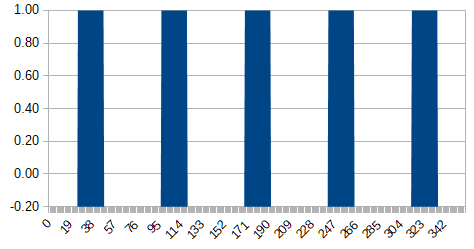
横軸にθ(0～360度)、縦軸にD(0～1)のグラフを書いて、この関係性を明らかにすることにします。まず、山のてっぺんの部分については、$D=1$とします。てっぺんとみなす角度の範囲は目測から22度としました(ざっくり)。

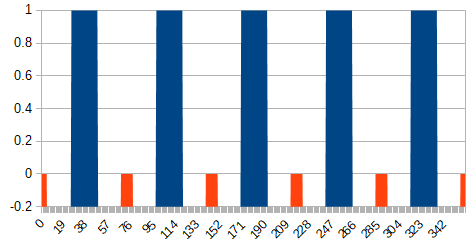
また、谷の底の部分については$D=0$とします。こちらはおよそ10度としました。グラフに映らなくて分かりにくかったので、Y軸の下限を-0.2としてあります。

オレンジと青の隙間の白い部分が山と谷の間の傾斜部分になります。この部分は曲線で0と1の間を埋めることになりますが、はてさてどのように埋めましょうか。数学的にこうだよ、と言えたらかっこいいのですが、私はそこまで頭がよくありません。ここはイージング関数を使っていい感じに埋めることにします。

参考: イージング関数チートシート

いろいろ試したところ、easeInOutQuadが見た目いい感じでしたので採用しました。

\begin{align}
y &= easeInOutQuad(x)  \\
&= 
\begin{cases}
2x^2  &(0 \leq x < \frac{1}{2}) \\
-2x^2 + 4x - 1 &(\frac{1}{2} \leq x \leq 1) 
\end{cases}
\end{align}

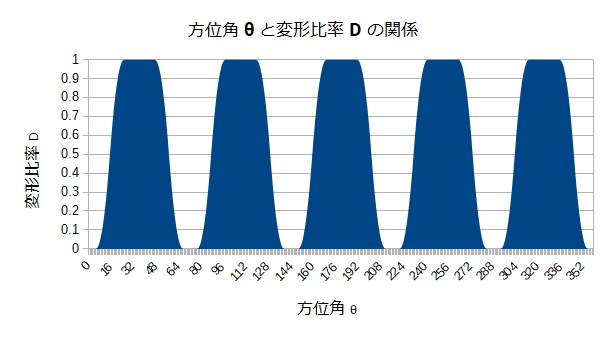
最終的なグラフは以下のようになります。縦軸の範囲は0～1に直したのに注意してください。

3Dモデル生成

ここまでで全方位における曲線が得られたので、あとはこれを使って3Dモデルを作ります。

まず方位角θを等間隔に刻んで(例えば1°毎に)、曲線を生成します。曲線はM個の点で離散化した座標を算出しておきます。2つの曲線の点について注目し、3つの点を選択して3角形ポリゴンを形成します。

完成！

このまま直接OpenGLなどで描画してもいいですが、今回はDXFフォーマットでファイルを書き出し、3Dモデリングソフトで表示させてみます。

今回はPythonでコードを書いたので、PythonでDXFフォーマットを扱えるezdxfライブラリを使用しました。出力したファイルをModoというソフトで表示したのが以下の画像です。

マテリアルを割り当て、レンダリングした結果がこちら¹。

こちらはBlenderで表示した結果です。AutoCAD DXF Importプラグインを有効にする必要があります。

※実は中心の部分はスプライン関数の影響で少し形がいびつだったので、コサインカーブを使って自然な感じに見えるように加工していますが、全体的な見栄えに影響しないので説明を割愛してあります。

横から見た感じはまあまあいいかな、という感じですが、底からの見た目はあんまし似ていないなーという感じですね。なんというか凹凸が足りないというか、丸みが乏しいせいかな。うーん……。

ソースコード

読む人はほとんどいないと思うので、畳んでおきます。

Pythonソースコードを見る

NumPy,SciPy,ezdxfのライブラリが必要です。

petaloid.py

from typing import List, Tuple
import math
import numpy as np
from scipy.interpolate import splprep, splev
import ezdxf


# 型ヒントの定義
Point2D = Tuple[float, float]
Point3D = Tuple[float, float, float]


def mix(a: float, b: float, x: float) -> float:
    """線形内分 x=0のときa, x=1のときb"""
    return b * x + a * (1.0 - x)


def easeInOutQuad(x: float) -> float:
    """Easing関数"""
    if x < 0.5:
        return 2.0 * x * x
    else:
        return -2 * x * x + 4 * x - 1


def calcDeformRate(t: float) -> float:
    """
    方位角tに対応する、曲線の変形比率Dを求める
    :param t: 方位角(単位は度)。72で割った余りが0のとき谷、36°のとき凸部分に対応
    :return: 変形比率D(0～1)
    """
    t = math.radians(math.fmod(t, 72.0))
    M = math.radians(72.0)  # 突起一つ分の角度範囲
    k = math.radians(5.0)  # 谷の部分の角度範囲
    tL = math.radians(25.0) - k  # 山の片側境界
    tR = (M - k) - tL  # 山の反対側境界

    if t < k or t > M - k:
        return 0.0  # 谷の部分
    elif t < k + tL:
        return easeInOutQuad((t-k) / tL)  # 傾斜
    elif t < tR:
        return 1.0  # 山の部分
    else:
        return easeInOutQuad(((M-k) - t) / tL)  # 傾斜(逆向き)


def curve(angle: float, div_num: int) -> List[Point2D]:
    """
    指定された方位角に応じた外形曲線を算出する
    :param angle: 方位角(0～360°)
    :param div_num: 曲線を構成する点の数。多いほど滑らか
    :return: 曲線を表す点列
    """

    # degree -> radian
    angle = math.fmod(angle, 360.0 / 5)  # 5角形なので360度を5等分

    # 方位角に対応する変形比率Dを求める(谷でD=0、山でD=1)
    D = calcDeformRate(angle)

    # 各制御点の変形比率を求める
    # 谷の部分では全ての制御点が左の比率(1.0)で、円弧となる
    # 山の部分では全ての制御点が右の比率で、規定の曲線を描く
    # それ以外の部分(山の傾斜部)ではDの値に応じて補間された曲線が描かれる
    r_rate = [
        mix(1.00, 1.00, D),
        mix(1.00, 1.05, D),
        mix(1.00, 1.18, D),
        mix(1.00, 1.46, D),
        mix(1.00, 1.36, D),
        mix(1.00, 1.18, D),
        mix(1.00, 1.07, D),
        mix(1.00, 1.01, D),
        mix(1.00, 1.00, D)]
    # 制御点の位置を求める
    xs = []
    ys = []
    n = len(r_rate)
    for i in range(n):
        deg = i * 90.0 / (n - 1)
        rad = math.radians(deg)
        x = r_rate[i] * math.sin(rad)
        y = r_rate[i] * math.cos(rad)
        xs.append(x)
        ys.append(y)
    # 全ての制御点を通るように、3次のスプライン曲線を引く
    spline = splprep([xs, ys], s=0, k=3)[0]
    detail = np.linspace(0, 1, num=div_num, endpoint=True)
    ix, iy = splev(detail, spline)
    points = list(zip(ix, iy))
    return points


def main():
    # 中央底部の微小突起を作る
    num_bottom_point = 8  # 中央底部の微小突起の点数
    bottom_width = 0.2  # 中央底部のサイズ
    bottom_height = 0.05  # 中央底部の高さ
    bottom_points = []
    for i in range(num_bottom_point):
        n = i / num_bottom_point
        angle = n * math.pi
        x = n * bottom_width
        # cosを使ってY=[1.0,1.0+height]のカーブを作る
        y = 1.0 + (math.cos(angle) + 1) / 2 * bottom_height
        bottom_points.append((x, y))

    # ペタロイド図形を表す3次元の頂点リストを作る
    num_curve: int = 180  # 方位の分割数(360なら1度毎, 180なら2度毎)
    num_point: int = 50  # 1方位における曲線の近似点数(中心点含む)
    num_point_curve = num_point - num_bottom_point  # (中心点除く)
    aspect_adjust: float = 0.75  # 縦横比率の調整値
    vertices: List[Point3D] = []
    for i in range(num_curve):
        # 各方位毎に曲線を求める
        theta_deg = 360.0 / num_curve * i
        theta_rad = math.radians(theta_deg)
        points1 = curve(theta_deg, num_point_curve)

        # 中心部の微小突起と連結する
        points2: List[Point2D] = [*bottom_points]
        for p in points1:
            # 曲線を横(X)方向に少し潰して、空いた分を平面とする(何とも微妙な処理……)
            x = bottom_width + p[0] * (1.0 - bottom_width)
            y = p[1]
            points2.append((x, y))

        # 3次元座標に変換する
        c = math.cos(theta_rad)
        s = math.sin(theta_rad)
        for p in points2:
            x2 = p[0]
            y2 = p[1]
            x3 = x2 * c
            y3 = y2 * aspect_adjust  # 縦横比率を調整
            z3 = x2 * s
            vertices.append((x3, y3, z3))

    # 3角形分割する
    indices: List[Tuple[int, int, int]] = []
    for angle in range(num_curve):
        a0 = angle
        a1 = (angle + 1) % num_curve
        for i in range(num_point - 1):
            i00 = a0 * num_point + i
            i01 = a0 * num_point + i + 1
            i10 = a1 * num_point + i
            i11 = a1 * num_point + i + 1
            if i != 0:  # 中心だけは3角形なので、重複しないよう除外
                indices.append((i00, i10, i11))
            indices.append((i11, i01, i00))

    # dxfで出力する
    # 折角vertexとindexに分けたが、dxfの3Dfaceでは頂点しか持たないので、
    # 頂点のリストを合成する
    triangles: List[Tuple[Point3D, Point3D, Point3D]] = []
    for i in indices:
        v1 = vertices[i[0]]
        v2 = vertices[i[1]]
        v3 = vertices[i[2]]
        triangles.append((v3, v2, v1))
    doc = ezdxf.new('R2010')  # MESH requires DXF R2000 or later
    msp = doc.modelspace()
    for t in triangles:
        msp.add_3dface(t)
    doc.saveas("petaloid.dxf")


if __name__ == '__main__':
    main()

残課題

私はもうこれ以上やる気はないのですが。もし、より完成度の高いペタロイドにチャレンジしたい奇特な人がいらっしゃいましたら参考にしてください。

• よりリアルなくびれの再現
  • 谷の部分の両端は実物を見ているともっとこう、くびれているように見えます。特に中心側の谷はUの字にくびれが入っていますが、今回はその点を考慮すると計算が複雑になりすぎて完成にこぎつけられないと思い断念しました。具体的にどうするかは分かっていませんが、方位角だけではなく、中心からの距離あるいは天頂角に応じて変化する要素を持たせるといいかもしれませんね。
• スプラインに依存しない形状作成
  • 今回はスプライン(多数の曲線のツギハギ)に頼ってしまったわけですが、実はもっと簡単な関数1つで表現できたりしないでしょうか。山の形はなんとなく4次関数っぽいなぁと思ったりするのですが、カーブフィッティングは試していません。
• メーカー毎の設計差異
  • 調べた限りだと、ペットボトルには規格が存在しないようです。キャップの口径は事実上の標準が定まっていて共通化されているようですが、ボトル自体の形状はメーカーに依存しているようです。今回使ったペットボトルはウィルキンソンのものなので、皆さんの手元にあるものと比べると違いがあるかもしれません。ただ、家にあるボトルは飲料メーカーによらずみんな同じ形をしているように見えますが(同じ容器メーカーの製品なのかも。寡占市場なのだろうか……)。

終わりに

Q. なんで底だけ？胴体は？
A. やる気が尽きました　_(:3」∠)_

1. DXFをimportした後、Mesh CleanUpを実行し、ポリゴンを結合しています。加えて、サブディビジョンサーフェスを用いて、形状を滑らかにしています ↩