雷を描く

CGで雷を作る方法について、まとめました。

実際に作ったものが上になります。

形を作る

雷っぽい形状を描くための、3通りのやり方を提示します。

1. 手で描く

おススメ度: ★★★★☆

原始的な手法ですが、ぶっちゃけこれが一番手っ取り早く、前提条件の少ない方法です(身も蓋もない)。

• メリット
  • 伸びる方法を自由に決められる
  • 開始点の数も枝分かれの数も自由
  • 太さ細さも自由自在
  • 少量なら短時間で描ける
• デメリット
  • センスが問われる
  • 大量に作るのは辛い

ネット上で「雷 描き方」と検索すると、いろいろ見つかりますが、やり方は実に千差万別で、奥の深さが伺えます。

2. 学術的な手法

雷の基礎知識

こういっちゃなんですが、専門的に学んだことはないので、大分適当なことを言っています。明らかに誤っている場合はコメントで指摘してください。

雷のメカニズム ←以下の説明よりこちらの記事をおススメ(図がついてるので……)

雷放電とは -雷放電の物理- ←より詳しく知りたい方はこちら

絶縁破壊

まず、絶縁破壊について説明します。絶縁体は電気を通しにくい物体のことを言いますが、物にはなんでも限度というものがあり、絶縁体でも高い電圧をかけると、イオン化してその結果電気を通してしまいます。絶縁体として有名なゴムにしろ、純水にせよ、程度の違いはありますが、絶縁破壊をおこします。空気もまた絶縁体ですが、高い電圧をかけると絶縁破壊され、電気を通します。

雷の通り道

雷の種類にはいろいろなものがありますが、ここでは下向きの負極性落雷というものについて説明します。この雷が発生する状況というのは、地表近くの空に負の電荷が、地表には正の電荷が集まっている状況です。負の電荷(空)と正の電荷(地表)の間は絶縁体の空気で満たされています(コンデンサみたく)。

この状況で負の電荷がたくさん集まり、電圧が高くなると、空気の絶縁破壊が始まります。

空気にも水分の多い少ないといったムラがあったり、ゴミが混じっていたりと、均一ではないので、絶縁破壊が起きやすい場所から順番に破壊が進んでいきます。これが雷がジグザグの形状となる理由と言われています。

絶縁破壊は1か所だけではなく、複数の箇所で発生していくので、形状は木のような枝分かれ状(根っこが上で逆さまになってしまっていますけど)になります。

ちなみに、空気を1mm絶縁破壊して進むのに約3000V必要らしいです¹。100万Vでも30cmちょいしか進めないんですね。

いろいろ省いていますが、本記事内ではこれだけ分かれば困ることはありません。

DBM(Dielectric Breakdown Model)

おススメ度: ★★☆☆☆

Fractal Dimension of Dielectric Breakdown - Physical Review Letters

以上のような雷のメカニズムを物理的な計算モデルでシミュレートできるようにした代表的な手法がDBMです。この論文が発表されたのは1984年のことです。IEEEの論文なので、読むには購読できる大学等の組織に所属するか、個人で学会員になるか、約40ドルで論文を購入するかになります(私は買いました)。

避雷針への雷放電パターンのコンピュータシミュレーション

↑こちらのペーパーに大体の説明が書いてあるので、元論文読まなくても済みますけど。

GIF動画は上空を負の電荷(黒)、地表を正の電荷(白)とした雷の生成アニメーションです。正の電荷に向かって段階的に成長します。

この方法では空間をマス上に区切り、そのうちのある1点を最初の絶縁破壊済のマス(動画中の黄色)として登録します。破壊済みマスに隣接するマス(候補マス)に対して新たに絶縁破壊が発生するかどうかの判定を行ない、判定に成功したら破壊済みマスを増やして繰り返し伝播していきます。判定は確率に基づいて行いますが、①地表(動画の白い部分)に近づくほど破壊確率が高くなる、②古い部分の破壊確率は段々と減少する、という計算式になっています。

左: 絶縁破壊されたマスの集合, 右: 短い枝が暗くなるように色を調整したもの

大変分かりやすくて、しかもいい感じの形状が出来上がりますが、この手法めちゃくちゃ時間がかかるのであまりお勧めできません。1か所絶縁破壊が発生すると、そのたびに空間全体が平衡状態になるまで全体計算を繰り返す必要があるので、マスの総数が増えるほど劇的に遅くなります。計算量オーダーは繰り返し回数をn、マスの総数をGとすると、$O(n*G^{1.5})$と言われています²。Core i7-7700K(4.2GHz)で上の300x300の画像を生成するのに20分くらいかかりました。

• メリット
  • 理論に基づいたリアルな形状が得られる
  • 3次元にも応用可能
  • 空間の電荷を適切に決めてやれば好きな方向に伸ばすことができる
  • 枝分かれの複雑さもパラメータによって調整できる
• デメリット
  • 致命的に遅い

DBM高速改良版

おススメ度: ★★★★☆

DBMがあまりに遅いので、もう少し速いのがないか探したところ、ネット上で(たぶん)オープンアクセスの論文を1つ見つけたので紹介します。論文漁れる人ならもっといいものが見つけられるしれないのですが、私はそこまで情熱と金銭を投入できないので……。

Fast Simulation of Laplacian Growth

元のDBMだと毎回絶縁破壊する度に空間全体の電荷を再計算する必要がありましたが、この改良手法では破壊済みマスに隣接する候補マスだけ再計算することで圧倒的に計算量を減らしています。新しい候補マスの絶縁破壊確率は、開始点からの距離に応じて高くなるように定義されます。計算量オーダーは$O(n^2)$にまで縮みました²。これでも画像サイズが大きくなってくると辛いですが、DBMよりは格段に速くて実用的です。Core i7-7700K(4.2GHz)で上の300x300の画像を生成するのに約10秒程度で終わります(速い！)。

論文をそのまま実装すると、画像のように中心から放射状に広がる形状しか作れませんが、下側の確率を高めにするなど、バイアスをかけるようにしてやると、任意の方向に枝を伸ばすことができて、自由度が上がります。

• メリット
  • 素のDBMより格段に速い
  • 出来上がる形状もDBMと大きく変わらない
• デメリット
  • 2007年の論文なので、特許が存在するかもしれない(未確認)

DLA(Diffusion-limited aggregation)

おススメ度: ★★★☆☆

元論文: Diffusion-Limited Aggregation, a Kinetic Critical Phenomenon - Physical Review Letters
Qiita内で2つしかないDLAの記事
DLAってアートみたいだよね。綺麗だ。
Pythonで数値シミュレーション(2) - 拡散律速凝集(DLA)

DLAは拡散律速凝集と呼ばれている物理現象です。塊魂ってゲームを知っている方はそれをイメージしてもらうと分かりやすいでしょうか。知らない方は雪の結晶とか塩の結晶とかをイメージしてみてください。最初に小さな核があり、その周囲を大量の微粒子が飛び回っています(高校で習うブラウン運動)。核に触れた微粒子は核にくっついてしまいその一部になってしまいます。核は周りの微粒子を取り込みながらどんどん成長します。

最終的にできあがる形状は中央を根とする樹形状となります。DBMのものと大分似ていますね。DBMもDLAの一種なので当然と言えば当然なのですが。

DLAの場合、どこのマスが新たに形状に追加されるかはほぼ完全に乱数次第なので、制御が難しいですが、微粒子の初期位置を偏らせるなどの工夫をすることで、ある程度形状を思い通りに伸ばせるかもしれません。実装がザルなので300x300の生成に20秒くらいかかってしまいましたが、真面目に実装すればもっと早いかと思います。

• メリット
  • 素のDBMより格段に速い
  • 微粒子の配置方法次第で伸ばし方を制御できる
  • Web上に記事や実装がたくさんある
• デメリット
  • 枝分かれの細かさは調整できない
  • 微粒子の数と初期位置の調整が画像サイズによって異なるので調整が大変(正規化すれば楽になるはず)

その他調べたけど未確認の方法

• Visual Simulation of Lightning
  • パーティクルシステムとレイトレーシングにより雷の成長を描写する方法
• Efficient Rendering of Lightning Taking into Account Scattering Effects due toClouds and Atmospheric Particles
  • 雲の反射も考慮して描写する方法。らしい
• Fast Animation of Lightning Using An AdaptiveMesh
  • 不完全コレスキー分解付き共役勾配法という手法にEisenstat trickという計算量削減方法を適用することで高速に生成する。らしい。内容が理解できない
• 電界を考慮した稲妻のCGモデル
  • 絶縁破壊した点を中心に、距離Nの位置に新しい候補点を複数置くことで枝分かれをシミュレートする方式。途中まで実装したが、なんかうまく行かず放置

3. シンプルな手法

おススメ度: ★★★★☆

手書きはダルいが、学術的なやり方はリアルだけど処理が遅いし自由度が足りない。もうちょっと適当にそれなりの画像を生成する方法はないでしょうか。

破壊確率一定の手法

放電模様（リヒテンベルク図形）のシミュレーション - Lazy Life,Easy Exit

こちらのサイトで紹介している手法は、DBMやDLAと同じように、絶縁破壊が進むかどうかは確率で決まるというものですが、その確率は場所によらず全て一定というものです。

確率を全マスで固定値にしてしまうことにより、DBMなどとは枝の伸び方は大分異なってしまいますが、非常に高速に計算が終わります。300x300が0.3秒程度で生成できました。

確率にムラを持たせる

※ここから完全にオリジナル手法になります。場当たり感maxです。

上の手法は高速でいいのですが、ちょっと形状が規則的な感じなのがいただけません。もう少し不安定な感じにならないでしょうか。上の元記事でも触れられていますが、確率が固定値の場合、確率を低くしたとしてもあまり枝分かれの形状は複雑になりません。

であれば、局所的に確率にムラを作ることでもって形状をもう少し不規則にする方法を試してみます。

マスごとの絶縁破壊確率をグレースケール画像として表してみることにします。黒が0%、白が100%ということにします。固定値の場合は全体が1色で塗られます。

今回はバリューノイズと呼ばれるノイズを用いてこのような確率分布を作ってみました。別にバリューノイズじゃなくてもパーリンノイズ等でも同じような分布が得られるでしょう。これで生成した画像が以下になります。少しは不規則な感じが出たでしょうか。

手動で確率マスクを作る

上の画像を見ると、直感的に気づくかもしれませんが、この方法で作成した雷はほとんどの場合、確率の低い部分を避けるように伸びています。

逆に言えば、通ってほしい部分の確率を高く、通ってほしくない部分の確率を低くした画像を用意すれば、雷の通り道を簡単に制御できるというわけです。

こんな感じの手書き画像を用意して、この確率の通りに雷を生成させます。

灰色のところが30%です。左上のところから生成開始します。結果は以下の通りです。

多少インコースを走りがちですが、そこは確率画像の濃淡を調整すればなんとかなります。

色を塗る

どの方法を選ぶかは人によると思いますが、とりあえず形は出来たということにして、次は色を塗り方を考えてみます。手書きの場合は、各自センスのままに好きに塗ってください。

情報としては、根本を開始点とする木構造(双方向接続)を持っているものとします(2,3いずれの手法の場合も、絶縁破壊が発生する際に破壊元⇔破壊先の対応を記録しておけば用意できます)。

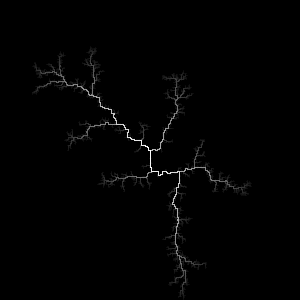
以下の画像は、3の手法を使って生成した雷の木から、一番長い枝だけを抜き出したものです。この形を使って例示していきます。

ガウシアンブラー(ぼかし)を使った方法

上の画像みたいにそのまま描画してしまうと、ドットのカクカクが気になってしまうので、ドット感を消すのと、雷ならではの光の拡散を表現するために、ぼかしを加えます。

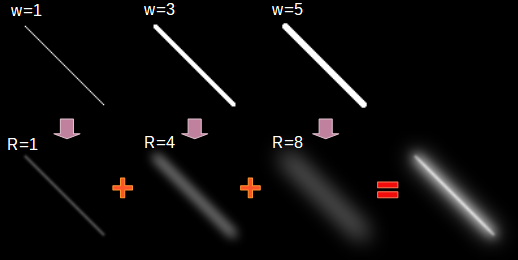
太さ1の線を描いた画像に半径1のガウシアンブラーを施します。次に太さ3の線を描いた画像に半径4のガウシアンブラーを施します。太さと半径を変えつつ、数段階分の画像を作ったところで全部を加算合成します。すると、ぼんやりと光る感じに仕上がるはずです。

太さと半径の関係と、何段階重ねるかについては、求める雷のくっきり度合いによって変わってくるので、丁度いい塩梅を模索してみてください。

適用してみると、幾分それらしくなったように感じます。人によってはまだちょっとドット感が残っているのが気にかかるかもしれませんけど。

静電ポテンシャルシミュレーションを使った方法

空間中に電荷$Q$を置くと、その電位$V$は距離に反比例して減少していきます($V=Q/r$)。$Q=1$とした場合に、電荷によって生じる電位の高低差を画像として可視化してみると以下のようになります。

グレースケールの画像ですが、電位1.0以上が輝度255(白)、電位0.0が輝度0(黒)になるように調整してあります。中央からぼんやりと光が広がる点光源のようには見えませんか？

これを雷の通り道にずらーっと配置して、電荷どうしの相互影響をシミュレートしてみれば、それっぽく雷が光っているように見えます。

通り道全部が全く同じ電荷値でもいいのですが、部分毎に数値が変わるように調整すると、太さを自由に変化させることができます。ただし、あまり変化が大きいとまだら模様になって汚くなるので緩やかに。

上のGIFは雷の開始点(左上)の電荷を0.5、終端(右下)を1.5として、中間の電荷は線形に変化するように補間したものです。左上が細く、右下が太くなり、少しダイナミックさが生まれたと思います。GIFは3枚の画像で構成されていて、それぞれ電荷に1.0倍、0.5倍、0.1倍の補正が掛かっています(ピカッと光って消えるように)。これだけでも大分それらしくなったのではないでしょうか？

具体的なシミュレートの方法については、ラプラス方程式をガウス・ザイデル法で解く方法により実現します。一見難しそうに見えますが、簡単な計算を変化がなくなるまで繰り返すだけのシンプルなアルゴリズムです。

差分法によるラプラス方程式の解法 - 秋田工業専門学校(ここの2.3節。これが一番わかりやすい)
[Pythonによる科学・技術計算] 静電位に対する2次元ラプラス・ポアソン方程式のヤコビ法による数値解法，楕円型偏微分方程式，境界値問題
世界一易しいPoisson方程式シミュレーション - 東海大学(ポアソン方程式はラプラス方程式よりちょっと複雑なバージョン。内容は大体同じだから参考になる)

なお、この手法は見た目がそれらしくなるので紹介しただけで、特に学術的にこうするのが正しい、というわけではありません。正しい方法は知らないので誰か教えてください。

加えて、ガウス・ザイデル法は普通に適用すると$O(n^3)$(たぶん)なので、画像サイズが大きくなると如実に遅くなります。画像中に疎な部分が多いと思うので、処理を工夫すればもっと早くなるとは思いますが。

ソースコード

C++でベース部分を書き、それをPythonから利用できるようにしたライブラリとPythonによるサンプルがあります。両方の言語が分からないと扱いづらいは思いますけれど、まあ、参考までに。

• コア部分
  • データ構造: header, source
  • 絶縁破壊処理部: header, source
• アルゴリズム
  • バリューノイズ実装: header, source
  • ガウス・ザイデル法による静電シミュレーション実装: header, source
• 絶縁破壊モデル
  • 共通インターフェース: header, source
  • DBM実装例: header, source
  • DBM高速改良版実装例: header, source
  • DLA実装例: header, source
  • バリューノイズ版: header, source
• 汎用(Python)
  • ガウシアンぼかしによる簡単雷描画メソッド: source, example
  • 静電ポテンシャルによる簡単雷描画メソッド: source, example1, example2

最後の2つのメソッドは直線を描くような気軽さで雷(の枝1本)を描けるようにしたもので、とりあえずこれだけ使うだけでも十分価値があると思います。

参考文献

音羽電機工業株式会社 編、横山 茂 著、石井 勝 著「写真で読み解く雷の科学」オーム社(2011年)

終わりに

雷といっても、人によってイメージするものは少しずつ違うと思うので、この方法さえあればオッケーというのは存在しないと思います。ここで提示した方法を参考に、自分なりの雷を生み出してみてください。

本記事の内容については具体的に書くと長くなりすぎるために、大分省略して書いてしまったので、詳しいところが知りたい場合はコメント欄、Twitter、メール等で気軽にお尋ねください。

---

1. https://hypertextbook.com/facts/2000/AliceHong.shtml ↩

2. http://gamma.cs.unc.edu/FRAC/laplacian_large.pdf P.5 TABLE.1 ↩