やりたい事
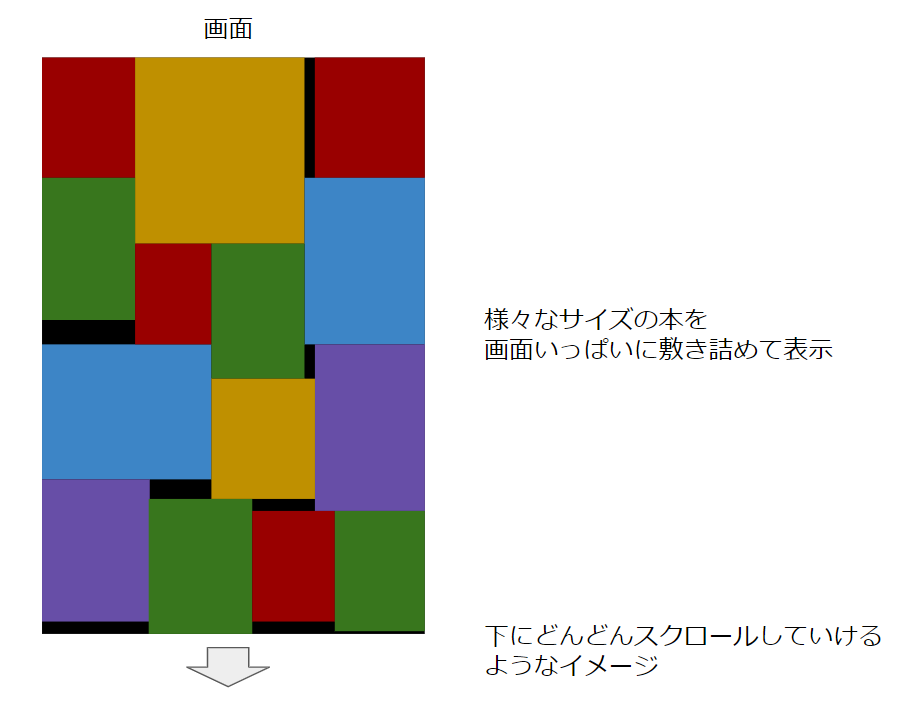
- 書籍画像を任意のスコアリング方法でリサイズして、画面いっぱいに埋めたい。
- 画面をスクロールして使うアプリを想定しているので、下から(または上から)積み上げていくような方法が良い。
製品イメージ
できるだけ隙間は少なくしたいので
- 矩形をある程度の範囲でリサイズする
- ちょっと重ねてもよいことにする
などのアイディアはあるが、実装難しそうなのでいったん保留。
問題への落とし込み
2次元のパッキング問題とか、矩形パッキング問題とか言われる問題に落とし込めることが判明。
https://qiita.com/nossey/items/0c1134a1cb287b035658
ここで紹介されてる方法がよさそう。
http://www.orsj.or.jp/archive2/or63-12/or63_12_762.pdf
結論
長方形詰込み問題を
- Bottom-Left法で
- Pythonを用いて
- 自分なりの実装法で
解いてみた。
製品イメージでは上に詰め込んでいく感じだが、
紹介されてる法では下から積み上げていくような感じなので、そちらで考える。
(製品に落とし込むときに逆にして読み替えればよい)
解き方
BL法
上記記事内には、bottom-left法とは
空の容器から始めて,図形に対して与えられた順序の先頭から順番に一つずつ図形を配置していくという貪欲法である.
図形を配置する場所は,その図形を配置しようとする時点において配置可能な場所の中の最も下の位置で,
そのような場所が複数ある場合は,その中で最も左の場所に配置する.
とある。
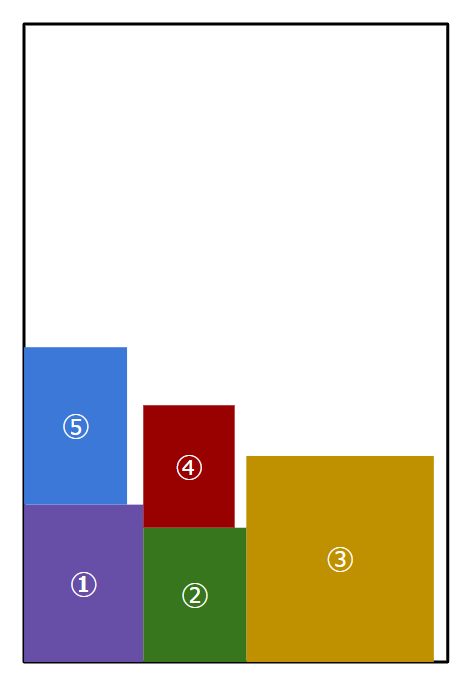
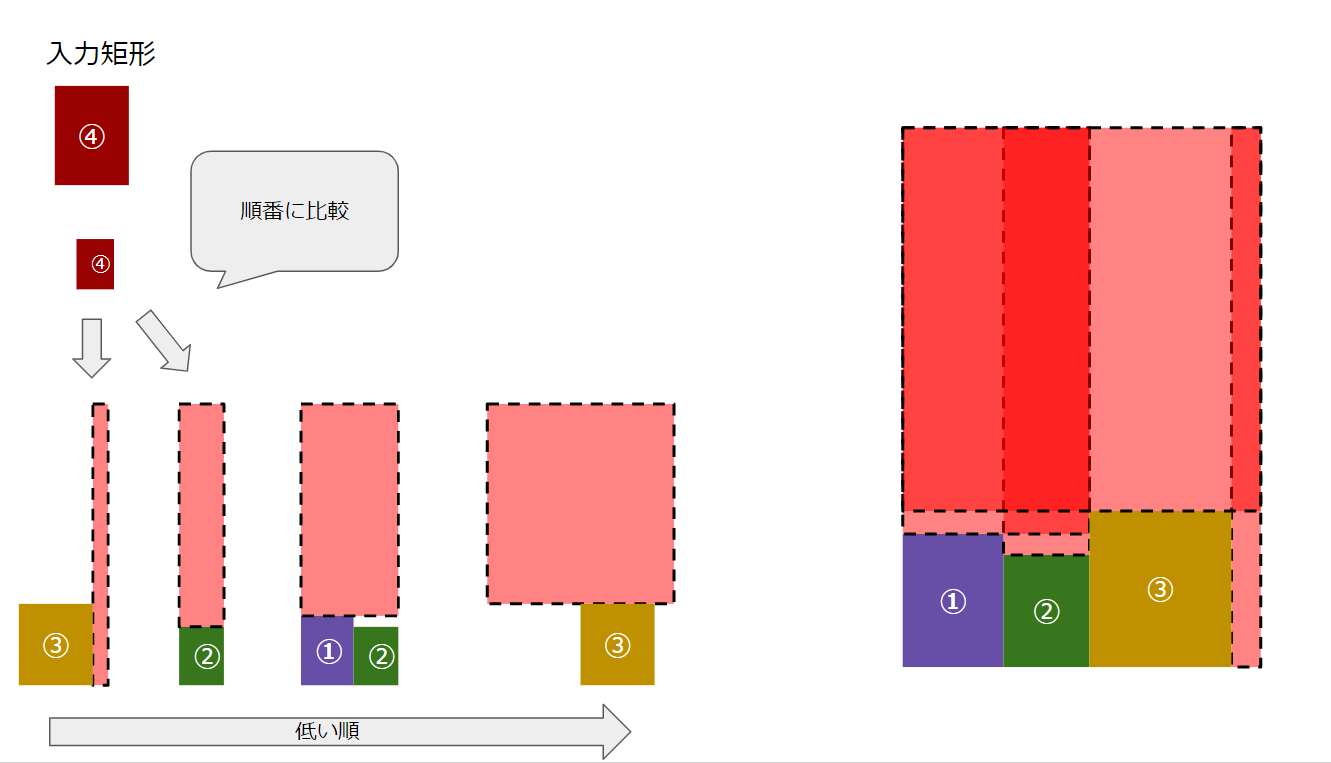
例えば以下の例では、
- まずは①を左下に配置
- その右に②、③と配置していき、
- ④を置く隙間がなくなったので一番低くおけるところ(②の上)に左詰めで配置。
- ⑤を配置する際は、①の上が一番低くなるのでそこに配置。
のように詰め込んでいく。
シンプルな方法で考えると
シンプルに考えると、
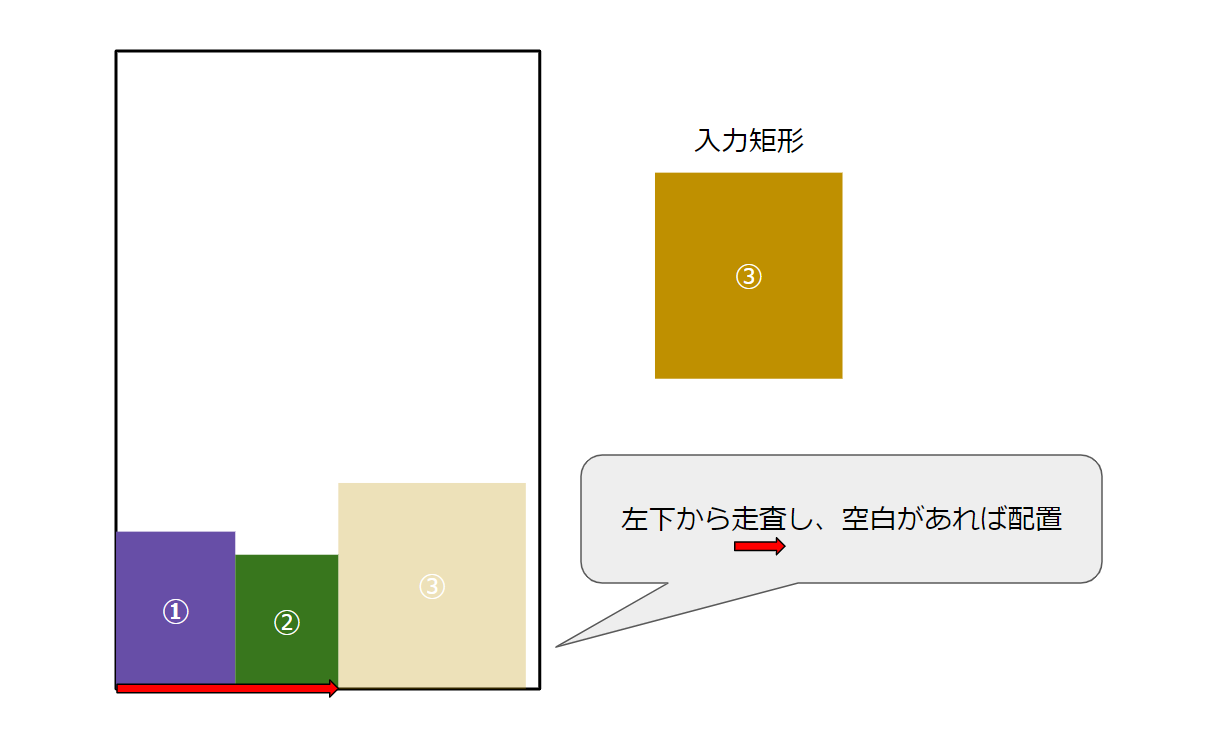
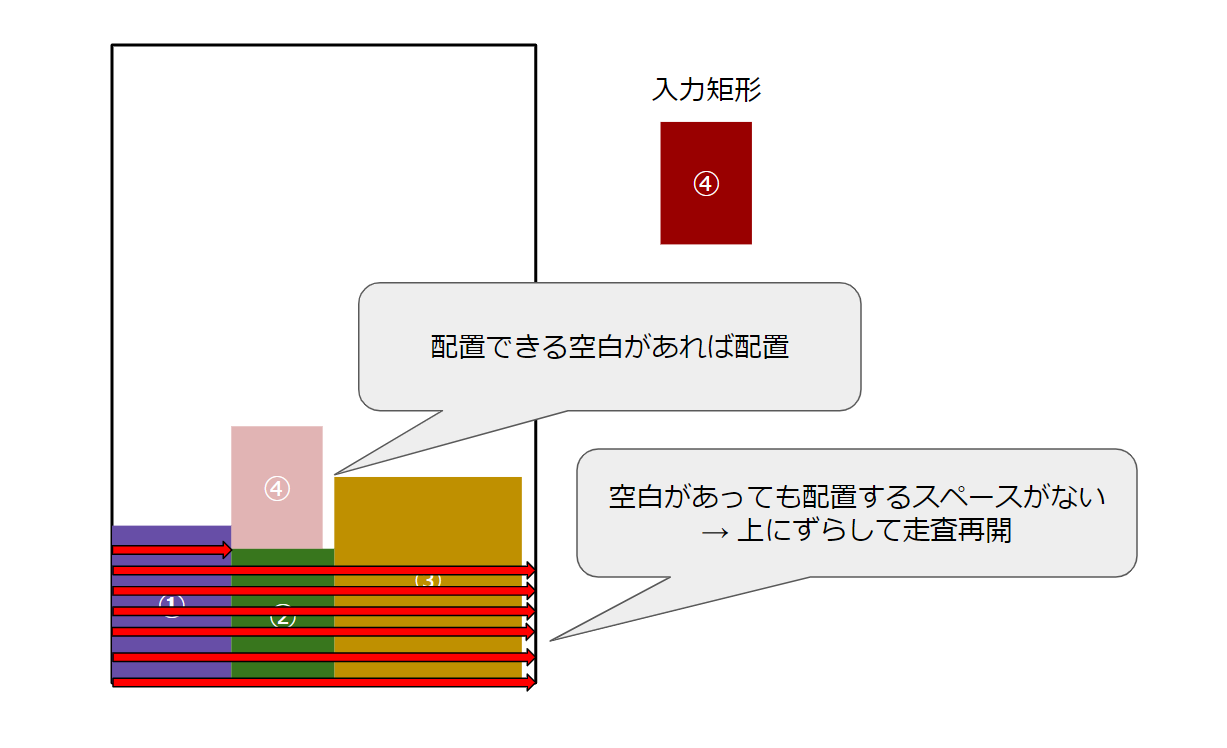
- 配置すべき矩形が与えられる
- 一番下の座標を、左から走査
- 空白になっている部分があれば、矩形を配置するほどの幅(と高さ)があるかを判定
- あれば、そこに配置し空白部分を上書き
- なければ1 point上の座標に遷移し、また左から空白を走査
シンプルに考えれば、容器の大きさのマトリックスを持っておき、座標が空白かそうでないかを記憶しておけば
上記のアルゴリズムを実装できる。
問題点
- ナイーブな実装をすると、1ピクセル毎に走査しなくてはならないため無駄
- 効率化として、「容器の底辺と図形の上底の座標を記憶しておけば、基本的にそのY座標(上下方向)だけを走査する」という方法があるが、依然としてマトリックスが必要そうなので重そう
私なりの解法
「マトリックスを持つのではなく、空白部分を矩形で管理し、入力矩形とマッチングしていく。」
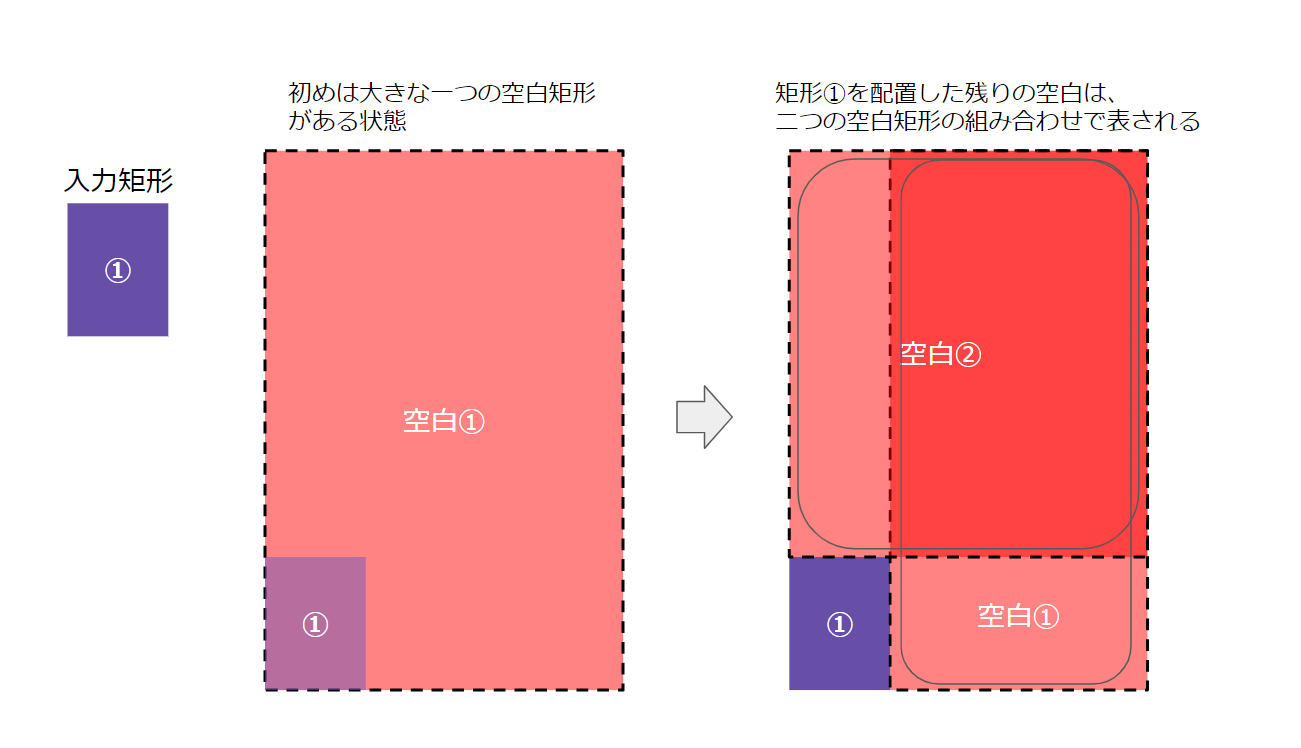
どういうことかというと、
- 空白を矩形として管理する
- 一番低い位置にある空白と入力矩形を見比べていく
- 空白にすっぽり入るなら、その空白の左下に矩形を配置
- その空白を分割し、二つの空白矩形をリストに追加する
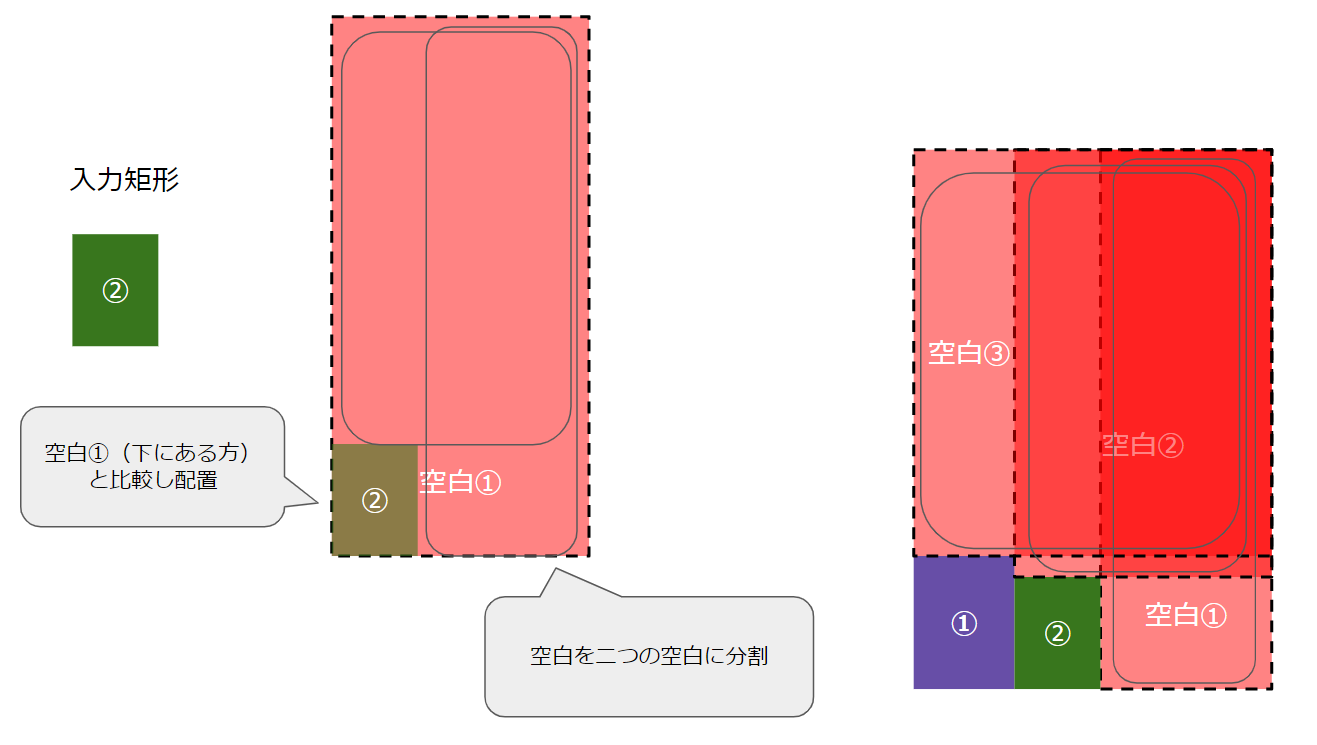
比較し配置した空白矩形を二つに分割するが、これだけでは不十分。
配置した部分に重なる空白矩形すべてに対して、分割しなければならない。
コード
Rectというclassを作成した。
class Rect:
def __init__(self, x, y, w, h):
self.x1 = x
self.y1 = y
self.x2 = x + w
self.y2 = y + h
self.w = w
self.h = h
def overlap(self, b):
return max(self.x1, b.x1) < min(self.x2, b.x2) and max(self.y1, b.y1) < min(self.y2, b.y2)
def subtract_by(self, b):
if self.overlap(b):
rooms = []
if (self.x1 < b.x1 and b.x1 < self.x2) and max(self.y1, b.y1) < min(self.y2, b.y2):
rooms.append(Rect(self.x1, self.y1, b.x1 - self.x1, self.h))
if (self.x1 < b.x2 and b.x2 < self.x2) and max(self.y1, b.y1) < min(self.y2, b.y2):
rooms.append(Rect(b.x2, self.y1, self.x2 - b.x2, self.h))
if (self.y1 < b.y1 and b.y1 < self.y2) and max(self.x1, b.x1) < min(self.x2, b.x2) :
rooms.append(Rect(self.x1, self.y1, self.w, b.y1 - self.y1))
if (self.y1 < b.y2 and b.y2 < self.y2) and max(self.x1, b.x1) < min(self.x2, b.x2) :
rooms.append(Rect(self.x1, b.y2, self.w, self.y2 - b.y2))
return rooms
else:
return [self]
def include(self, b):
return self.x1 <= b.x1 and b.x2 <= self.x2 and self.y1 <= b.y1 and b.y2 <= self.y2
def larger_than(self, w, h):
# 座標は関係なく、図形として入るかどうか
return w <= self.w and h <= self.h
def __str__(self):
return "({}, {}, {}, {})".format(self.x1, self.y1, self.w, self.h)
Rectのメソッド説明
a = Rect(...)
b = Rect(...)
という矩形を定義したとき
-
a.overlap(b)- aとbが重なるかどうかを判定
-
a.subtract_by(b)- aからbを引いたときの、残りの領域を表す矩形のリストを返す
- 空白を分割するときに使う
-
a.include(b)- aがbを完全に包含するかどうかを判定
- 重複する空白、無意味な空白を削除するときに使う
-
a.larger_than(w, h)- aが(幅, 高さ) = (w, h)で表される図形を含められるか判定
- その空白に入力矩形を配置できるかどうか判定するときに使う
使い方
def put_rect(input_rects, roomsORIG=[Rect(0, 0, 1024, 10000)]):
'''
空間にBottom-Left法で矩形を配置しその位置のリストを返す。
Parameters
----------
input_rects: [(int, int)]
(width, height)で表される入力矩形のリスト
rooms: [(int, int, int, int)]
(x, y, width, height)で表される空白矩形リスト。配置可能空間を示す。
Returns
-------
rects: [int, int, int, int]
(x, y, width, height)で表される配置した矩形リスト
rooms: [int, int, int, int]
(x, y, width, height)で表される空白矩形リスト
'''
# 空白矩形と比較し、配置可能な空白を探索
rects = []
uniq_rooms = list(roomsORIG)
for input_rect in input_rects:
for i in range(len(uniq_rooms)):
room = uniq_rooms[i]
if room.larger_than(input_rect[0], input_rect[1]): #このrectに配置可能
new_rect = Rect(room.x1, room.y1, input_rect[0], input_rect[1])
rects.append(new_rect)
break
# すべての空白矩形から subtractする
new_rooms = []
for room in uniq_rooms:
new_rooms += room.subtract_by(new_rect)
new_rooms = sorted(new_rooms, key=lambda x:x.y1) # 結局総当たりするので意味ないが、将来効率化を考えソート
# 重複削除 総当たり
uniq_rooms = []
for r_i in new_rooms:
include_flg = False
for r_j in new_rooms:
if r_i == r_j: continue
if r_j.include(r_i):
include_flg = True
break
if not include_flg:
# print("{} は他のどれにも含まれない".format(r_i))
uniq_rooms.append(r_i)
# 低い順(左にある順)に並び替え
new_rooms = sorted(new_rooms, key=lambda a:a.x1)
uniq_rooms = sorted(new_rooms, key=lambda a:a.y1)
return (rects, uniq_rooms)
img_list = [(300, 350), (200, 300), (400, 400), (150, 250), (250, 400)]
rects, rooms = put_rect(img_list, roomsORIG=[Rect(0,0,1024,10000)])
for rect in rects:
print(rect)
(0, 0, 300, 350)
(300, 0, 200, 300)
(500, 0, 400, 400)
(300, 300, 150, 250)
(0, 350, 250, 400)
まとめ
- 長方形詰込み問題を空白を管理することで効率的(?)にPythonで解いた。
- 小さすぎたり、細すぎたりする空白矩形は削除してしまうなど、さらなる効率化はありそう
- すぐにできる効率化は、重複比較部分で総当たりをしている部分。
パズルみたいで面白かった。
iOSアプリで製品を作る予定なので、Swiftに移植したらそちらも投稿します。