この記事はSFC-RG Advent Calendar 2017の5日目です。

「ブロックチェーンは高改ざん耐性を持つ」

以上のような言説をよく目にする。所謂51%攻撃は困難であるため、改ざん耐性を持つ、という説明がそれは一定以上事実ではあると思うが、それがホワイトペーパどんな説明がされているか。今回は、基礎知識の簡単な説明をしつつ解説する。式がすこし出てくるが、筆者も概ねの理解でまだ全てを理解できているわけではない。数式の意味を概ねでも理解していくことには非常に意味があると考えているので、その辺りを追えたら喜ばしい限りである。

ホワイトペーパーはたかだか9ページなので一読すると良い。

ホワイトペーパーでの改ざん耐性の説明

ホワイトペーパーでは、11. Calculationsの項目で説明されている。ざっくり説明されていることをまとめると以下のような感じだ。

現在採用されている善意のチェーンとは別のチェーンを攻撃者が生成する
攻撃者が生成するスピードが、善意のチェーンが生成されるより早くなる可能性を考える
善意のチェーンと攻撃者のチェーンの競争は二次元ランダムウォークである
攻撃者のチェーンは負けている状態から始まる（過去のブロックを改ざんする）
攻撃者のチェーンが追いつく確率は、ギャンブラーの破産問題で計算できる
過去のブロックが改ざんされ、自分への送金が取り消される可能性が十分に低くなる可能性を知りたい
zブロック前のブロックが改ざんされる可能性ポアソン分布を用いて算出できる
攻撃者が善意のチェーンを追い抜かれる可能性は過去のブロックであればあるほど指数関数的に低くなる

数学用語がちょこちょこ出てきてなんのこっちゃ、となる。簡単に説明を加えながら少しづつ見ていこう。

ブロックチェーンを改ざんする状況

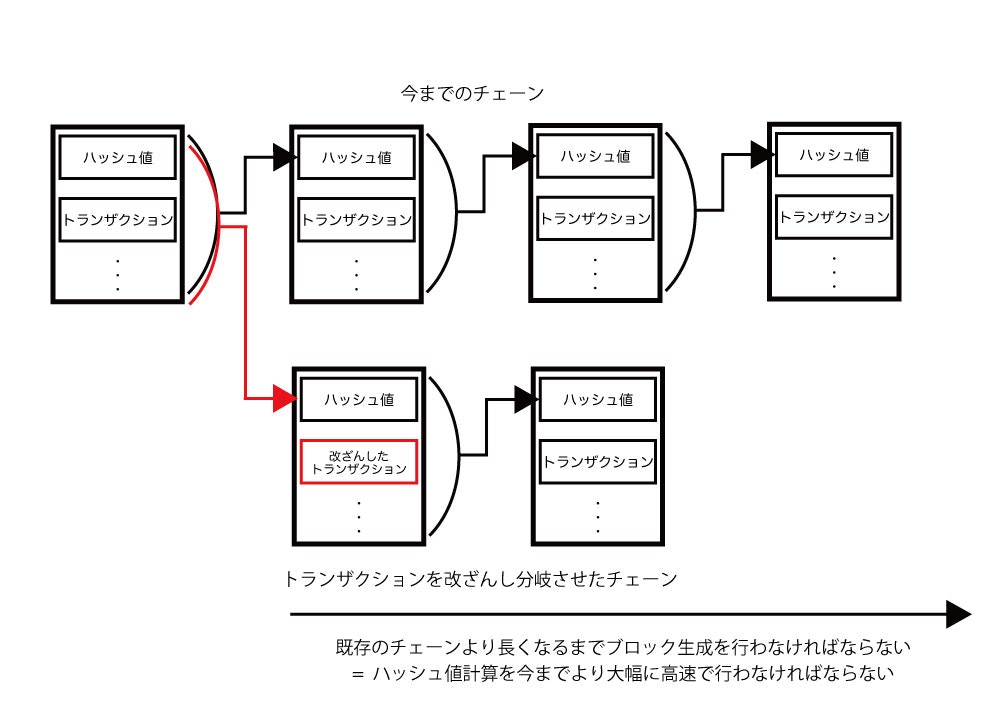
ブロックチェーンの基礎的な部分だが、ブロックチェーンは典型的にはより長いチェーンが採用される。正確には、そのブロックまでの累積difficultyが高いチェーンが選択される。下図に示すように、過去のトランザクションを改ざんすれば、まずは現状採用されてるチェーンよりブロックを長くする必要があるのだ。また、改ざん後のチェーンが追い抜いた後も、以前のチェーンではなくそちらを信頼させ、維持し続ける必要がある。

そのためには、善良なノードよりも早く攻撃者はブロックを生成し続ける必要がある。そこで、ホワイトペーパーでは、攻撃者と善良なノードがそれぞれブロック生成間隔時間(Bitcoinでは10分)以内に生成できる確率を変数と置くことで、攻撃者が生成するチェーンが追いつかれる可能性の推定を行っている。

攻撃者のチェーンが追いつく確率

善良なノードがチェーンを伸ばし、それに攻撃者が過去のブロックからチェーンを伸ばしていく様をホワイトペーパーでは「競争」として述べられている。

二次元ランダムウォーク

この競争は、二次元ランダムウォークであるとされている。ランダムウォークとは、一定の確率で起こる事象を繰り返す事象においての確率のモデルである。例えば、コイントスでの裏表の確率はそれぞれ$\frac{1}{2}$だ。そこで、表だったら$+1点$、裏だったら$-1点$であるようなゲームで特定点数になる際の確率を求めるなどの事例で使われる。

ブロックチェーンの改ざんの事象では、以下のような条件となる。

攻撃者と善良なノードがそれぞれブロックを生成できる確率
改ざんするブロックが最新から何ブロック前かを持ち点とする
攻撃者がブロックを生成できればブロックを$-1点$
善良なノードがブロックを生成できれば$+1点$

この時に持ち点が$0点以下$になる確率を求めることで、攻撃者のチェーンが追いつき、追い越す確率を求めることができる。

ギャンブラー破産問題

ここで、追いつく確率はギャンブラーの破産問題を用いて求められる。ギャンブラーの破産問題とは、ランダムウォークである事象をコイントスなど確率的事象で行うギャンブルとし、持ち点が0以下、つまり破産する確率を求める有名な問題である。

ブロックチェーンでは、先述の条件として考えれば同様の問題であることがわかるだろう。これを定式化するると以下の式になると述べられている。この式の導き方は、ここで示されている。

$p$ = 善良なノードが先にブロックを生成する確率
$q$ = 攻撃者が先にブロックを生成する確率 $(p+q=1)$
$q_z$ = 最新から$z$ブロック前のブロックを改ざんし、追いつく確率

q_z = \left\{ \begin{array}{ll} 
1 & if\hspace{3mm} p\le q \\ 
(q/p)^z & if\hspace{3mm} p>q 
\end{array} \right\}

ブロックを生成する確率は、正確にはProof-of-Workにおける、ブロックのハッシュ値が目標値以下になるノンスを攻撃者/善良なノードより先に発見できる確率である。発見するためには、連続でハッシュ計算を行っていくしかないため、その速度が早ければ発見できる確率は高くなる。そのため、p、qはそれぞれ善良なノード、攻撃者の持つハッシュパワーの割合と同値と考えられる。

つまり、$p \le q$の状態は攻撃者が50%以上のハッシュパワーを持った状態のことである。その際は必ずチェーンが追いついてしまい、改ざんが成功してしまうことを示している。所謂51%攻撃だが、正確には50%攻撃であることが示されている。

必要な承認回数は？

善良なノードがあるチェーンを持っていた時、攻撃者が今どのくらい追いついているのかを知り得る手段はない。例えばあるトランザクションで幾らかのBTCを受け取った後、数ブロックが連なっている状態で、誰かに送金したいとする。この時、攻撃者がすでに攻撃を始めていて、実は改ざんが成功する間近だったとしても、善良なノードはそれを知りえないのである。

つまり、今どのくらい改ざんされる危険性が迫ってきているのか判断が先ほどの計算式だけでは、わからない。自分のトランザクションがブロックに格納されチェーンに繋がれた後、後続のブロックが繋がれることを「承認」と言われている。したがって、ここではいくつ承認されたら過去のブロックが改ざんされにくいのか、ということを確率的に示したい。

ポアソン分布

ポアソン分布とは、ある事象が一定の確率で起こる時、単位時間内に何回起こっているかの確率を示す分布のことである。ここでは、使いたいトランザクションが$z$ブロック前にある時、攻撃者が$k$ブロックのフォークしたチェーンの生成を終えている確率を求めるために用いる。単位時間内に$\lambda$回起こる事象が、$x$回起こっている確率を示すポアソン分布の公式は以下である。

f(x) = \frac{e^{-\lambda}\lambda^x}{x!}

ここで、単位時間は使いたいトランザクションが$z$ブロック前にあるため、$z$ブロック分の生成間隔時間となる。つまり$z$はブロック数であると同時に善良なノードが$z$個のブロックを生成した単位時間を示す。善良なノードが1ブロック生成する間に、攻撃者は$q/p$の確率でブロックを生成できる。したがって、$z$単位時間内には$z \times q/p$回起こっている。これをポアゾン分布の公式に当てはめると、以下である。以下の式で$z$ブロック前のブロックが生成されて以降、$k$ブロックを攻撃者が生成している確率を示すことができる。

$p$ = 善良なノードが先にブロックを生成する確率
$q$ = 攻撃者が先にブロックを生成する確率 $(p+q=1)$
$z$ = 改ざん確率が知りたいブロックの後に連なるブロック数

\lambda = z \times q/p　\\
f(k) = \frac{e^{-\lambda}\lambda^k}{k!}

したがって、ある時点で$z$ブロック前のブロックが改ざんされる確率は、その時点で攻撃者が$k$ブロックの生成を終えている確率に、$z-k$ブロックを追いつく確率をかけたものをすべての$k$について足し合わせることで計算できる。式は以下の通りである。

\sum_{k=0}^\infty \frac{\lambda^k e^{-k}}{k!}\cdot 
\left\{ \begin{array}{ll} 
(q/p)^{z-k} & if\hspace{3mm} k\le z \\ 
1 & if\hspace{3mm} k\gt z 
\end{array} \right\}

この式を無限な足しあわせのないよう変形し、各変数の説明を再度示しながらまとめると以下となる。

$p$ = 善良なノードが先にブロックを生成する確率
$q$ = 攻撃者が先にブロックを生成する確率 $(p+q=1)$
$z$ = 改ざん確率が知りたいブロックの後に連なるブロック数

\lambda = z \times q/p　\\
1-\sum_{k=0}^z \frac{\lambda^k e^{-k}}{k!} 
\left\{ 1-(q/p)^{z-k}\right\}

改ざん確率の推定

改ざん確率の推定式ができたところで、実際に確率を求めてみよう。

ブロック数と改ざん成功確率

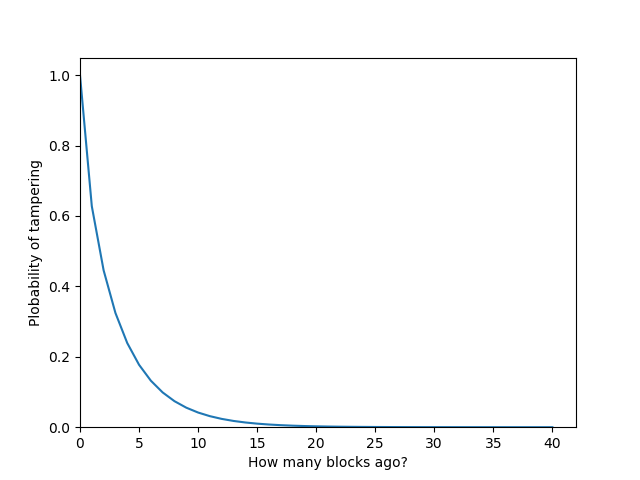
ホワイトペーパーでは、攻撃者が30%の確率でブロックを生成するとしての試算を行っている。その時の改ざん可能性が知りたいブロック以降に連なったブロック数と改ざん可能性のグラフは以下である。

指数関数的に$z$が増えると改ざん可能性が低くなっているのがわかるだろう。2017年12月現在の最大のハッシュパワーを持つマイニングプールは約18%だ(Blockchain.info参照)。このマイニングプールがもし攻撃者になったとしてもこのグラフよりも改ざん可能性は低くなる。

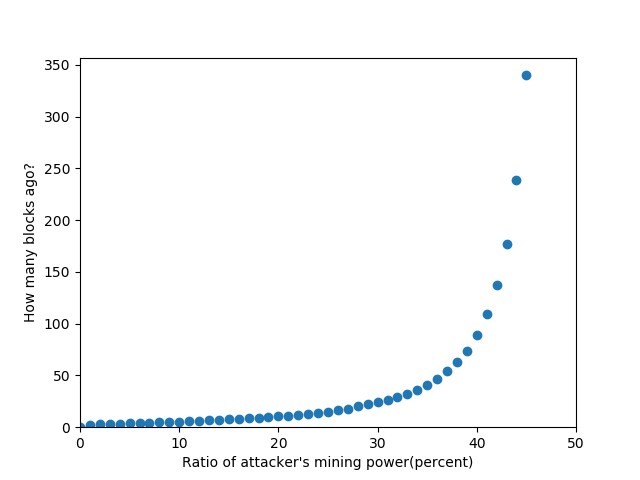
攻撃成功確率0.1%以下になるブロック数

次にホワイトペーパーでは、攻撃者が一定のブロック発見確率であった時（＝一定のハッシュパワーを持っていた時）攻撃成功確率が0.1%以下になるには、何ブロックの承認が必要かを求めている。実際に計算を行って、グラフ化したものが以下である。発見確率が50%に近くになるに連れて必要なブロック数は増加していくことが見て取れるだろう。

所謂6ブロック連なったら承認されたとみなす、という運用がある。これは、ホワイトペーパーの中で攻撃者が10%の発見可能性を持っている時、5ブロック連なることで0.1%以下の改ざん可能性になることからの運用である。しかし、先述のように現在最大のハッシュレートを持つマイニングプールは18%のハッシュレートを持ち、そのとき6ブロック連なっただけでは約0.8%の改ざん成功確率である。そのため、現在そのままの「6ブロックの承認」での運用をしても、設計当初の改ざん耐性を利用できてるとは言えない。

おわりに

今回改めて自分の勉強も兼ねて改ざん耐性についてまとめた。少し最後に触れたが、設計当初には想定されていなかった状況も起こりつつあり、改ざん耐性は当初の設計通りに満たされてるとは言い難い。また、近年のハッシュレートの急上昇は、たかだか数年で数倍のハッシュパワーが新たに投入されており、その時点での50%を最大のマイニングプールが超えていないとしても100%安心できるものではないということがわかるだろう。

広く言われていることではあるが、そもそも通貨という概念を確率論的にファイナリティを持ったとして、運用するのにはいろいろ問題がある。こうして改めて設計当初の改ざん耐性についてまとめることで、基盤としての課題を強く認識することができた。

Bitcoin Blockchainのホワイトペーパにおける改ざん耐性の推定