本記事は、プログラミング初心者の私がAidemyのデータ分析コースの最終成果物として、アサヒグループホールディングスの株価データの可視化・分析、さらに株価変動予測を行ったものです。
筆者は本業のコンサルティング業務において、特定の業界や製品の市場予測を調査する機会が多くあります。そんな中で「誰かが作った予測値を探すだけではなくて、自分でも予測値を算出できるようになれたらより納得感のある説明ができるようになれるはず」と考え、汎用性が高くコーディングが比較的シンプルなPythonの学習を始めました。
本記事は筆者同様、Python初心者で1週間(ゆるく進めて2週間)程度で完成する作業量のコードを作成してみたい方、株価データのグラフをたくさん作成し、コーディングの達成感を味わいたい方、時系列予測の手法を模索している方に読んでいただくことを想定しております。
目次
1.はじめに
2.事前準備(データの前処理)
3.株価データの可視化
4.テクニカル分析
5.株価予測
6.おわりに
7.(補足)Aidemy・教育訓練給付について
1.はじめに
【実行環境】
・Windows 11, version 22H2
・google colaboratory
【方法】
アサヒグループホールディングスの株価データ(2018年7月~2023年7月)を取得し、株価変動予測を行った。
・株価データの可視化では、mplfinannce、pytiライブラリを使用した株価データの可視化、TA-Libライブラリを使用し株価データの推移を確認する。
・テクニカル分析パートでは、Polityライブラリを使用したゴールデンクロス、デッドクロスの可視化により買い時、売り時の時期を確認する。
・株価予測パートでは、 Meta(旧Facebook社)が公開している時系列予測ライブラリProphetと機械学習手法のLSTMを使用して予測を行う。
【予測精度の結果】
・Prophetの予測結果は2023年下期以降も上昇傾向を維持し、2024年下期ごろには時価総額6,000円から7,000円程度で推移する結果となった。コロナ前水準へ回復に向かうという方向感は理解できるが、値幅が大きいためこの結果だけでは判断材料として弱い。
・LSTMの予測結果は、一度目の実行では後半にかけてコロナ禍の変動をうまく学習できず、実績値と予測値に大きな乖離が生まれた。二度目の実行では学習量(エポック数)を増やし、また学習のレイヤーを増やしたことにより実績値に非常に近い予測値が出力できた。ただし、この結果は株価のランダムウォークの特性を顕著に表すものであり、長期的な予測の精度は不明であるものの、ごく短期(少なくとも翌日)については予測不能かつ変数に影響が大きい事象(大規模災害・不祥事等)がない限り、予測可能と理解した。
・いずれの予測においても精度が高いものとは言い難い結果となった。
(※今回の分析では学んだコーディングの実践が目的であるため予測結果の確からしさの検証は対象外とする)
【改善点】
・分析対象について
アサヒグループホールディングスの株価のみを対象としたが、実際に投資判断を行う際には同業他社との比較や日経平均株価との推移との連関性の有無を検証する必要がある
・期間について
Prophet、LSTMのいずれも予測に使用する株価データの量を増やすことで結果が大きく変化するとは考えにくいが、検証する必要がある
2.事前準備(データの前処理)
まずはインターネット上から対象企業の株価データを取得する。
今回は無料で情報を入手したいため、Stooq(ポーランドの企業が運営する金融ポータルサイト)から、2502 アサヒグループホールディングス(株)の直近の株価データを取得する。
import pandas_datareader.data as pdr
df= pdr.DataReader("2502.JP","stooq")
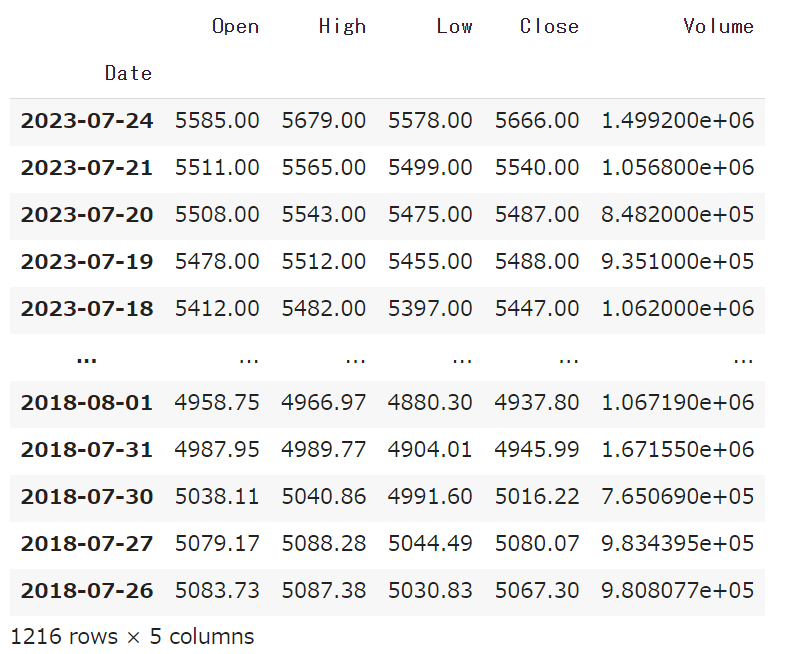
df
今回は時系列データとして株価データを使用するため、日付が降順になっているデータを昇順に変更する必要がある。
#まずは取得した株価のをデータフレームを日付けのインデックスで昇順にソートするメソッドを作成する。
def get_stock_data(code):
df = pdr.DataReader("{}.jp".format(code),"stooq").sort_index()
return df
#作成したメソッドにアサヒグループ(2502)を指定し、昇順に変更できていることを確認する。(最後の5行のみを表示)
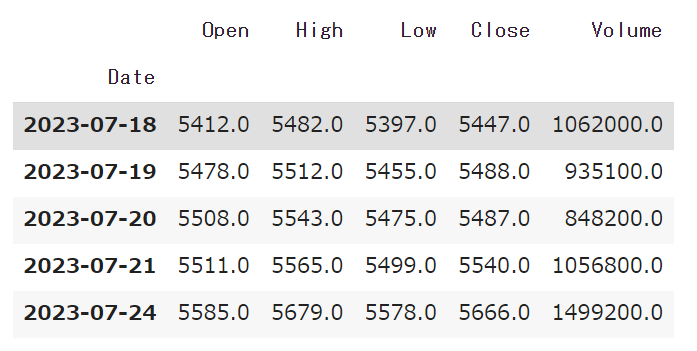
df=get_stock_data(2502)
df.tail()
#株価データの終値でグラフを作成し、株価の動向の大枠をつかむ
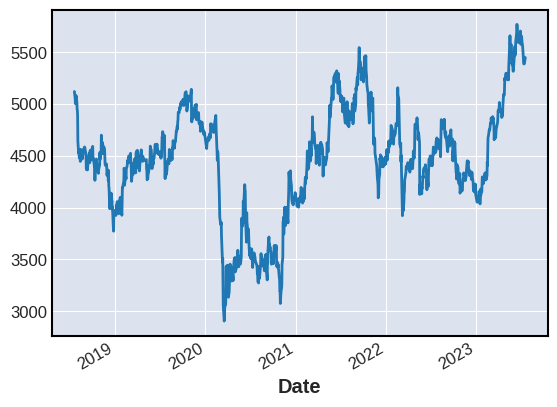
df["Close"].plot()
終値の推移グラフによると、アサヒGHDの株価は2020年前半に新型コロナウイルス感染拡大の影響により大幅に低下(約2,000円下落、40%減)していることが確認できる。また、コロナ前水準5,000円台まで株価が回復したのが2021年後半であることから影響が約1年半続いたといえる。
3.株価データの可視化
ここからは準備したデータを多面的に理解するため株価の動きを示す指標の可視化を行う
#株価データを可視化するため、金融データの分析ライブラリ(mplfinance)をインストールする
!pip install mplfinance
#株価データを取得して日足のローソク足チャートを表示する。データの対象期間は直近100営業日とする。
import mplfinance as mpf
df = get_stock_data(2502).tail(100)
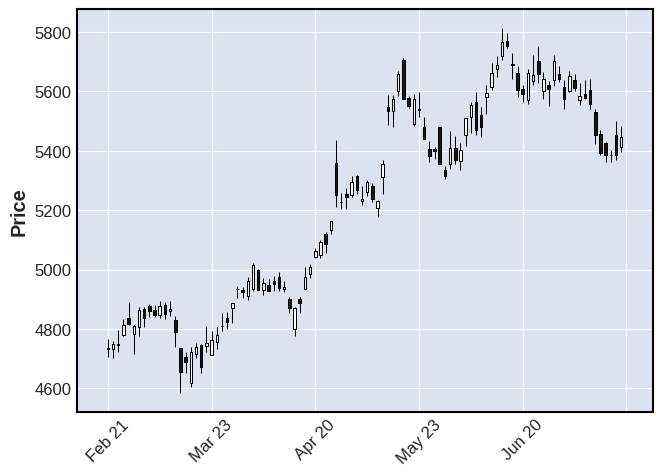
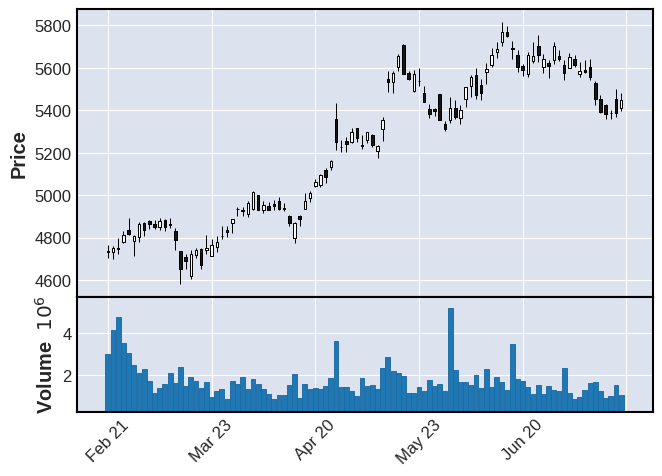
mpf.plot(df,type="candle")
ローソク足チャートによると、長い陽線が出たり、陽線が連続して出現したりすると株価が上がりやすく、長い下ヒゲがでると下落していた株価が上昇に転じやすい傾向があるといえる。
次に取得した株価データの出来高(一日に成立した売買の株数)と株価の推移を比較するグラフを作成する
mpf.plot(df,type="candle",volume=True)
出来高と株価の比較グラフによると、出来高が増加すると、数日後に株価が上昇していることがわかる。ここから出来高は株価の動向を分析する際の先行指標として機能しているといえる。
4.テクニカル分析
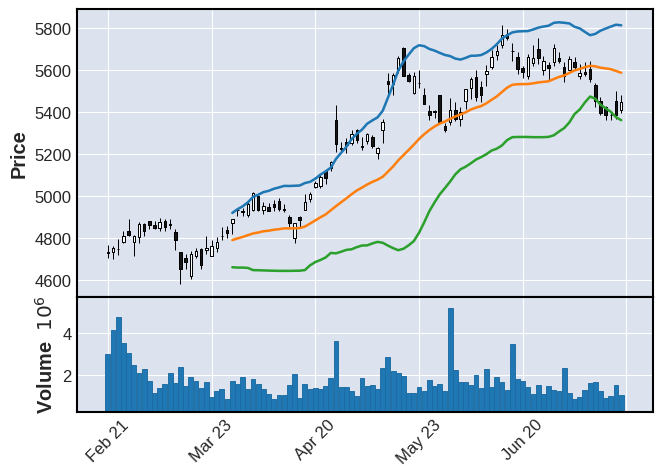
次に移動平均曲線(一定期間の株価の終値から平均値を計算して折れ線グラフで表したもの)を表示し、株価の大まかな動きをつかみ、今後の株価の動向を予測する。
#一定期間の終値の平均をとる単純移動平均線を使用し、サンプル期間は5日、25日、75日として3つの移動平均線を表示する
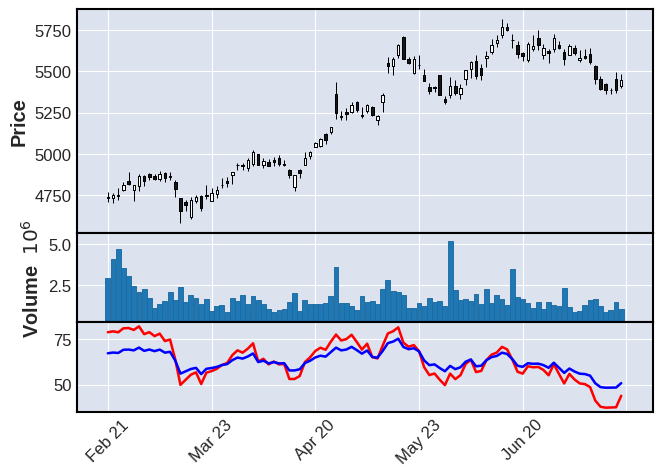
mpf.plot(df,type="candle",mav=(5,25,75),volume=True)
移動平均線は長期間だと平均値がならされているため線の上下が少なくなり、傾向を容易に知ることができる。
5日線はローソク足に沿った動きであるが、25日線と75日線は右上がりで株価が上昇傾向にあることがわかる。
線同士の関係性としては、5日線が下落して25日線に接するあたりで反発するように上昇に転じる動きがみられる
取得した株価をもとに買われすぎ、売られすぎを表すオシレーターを用いて株価を分析する
ここでは移動平均をもとにしたオシレーターの「ポリンジャーバンド」(相場のボラティリティを言って機関の株価から計算し、予想される株価の変動範囲をチャート上に表示する指標)を使用する。
#この指標を使用するため、計算ライブラリ「pyti」をインストールする。
!pip install pyti
#株価の変動範囲をバンド上限、ミッドバンド、バンド下限の3つを取得する
それぞれの計算クラスをbb_up、bb_mid、bb_lowの名前でインポートする。
from pyti.bollinger_bands import upper_bollinger_band as bb_up
from pyti.bollinger_bands import middle_bollinger_band as bb_mid
from pyti.bollinger_bands import lower_bollinger_band as bb_low
data = df["Close"].tolist() #終値をリスト型に変換
period = 25
bb_up = bb_up(data, period) #バンド上部
bb_mid = bb_mid(data, period) #ミッドバンド
bb_low = bb_low(data, period) #バンド下部
#pytiライブラリのクラスでは、共通して終値のリストと期間を引数にする書式をとる。
df["bb_up"] = bb_up
df["bb_mid"] = bb_mid
df["bb_low"] = bb_low
#計算したポリンジャーバンドを単体で確認する
df[["bb_up","bb_mid","bb_low"]].plot()

#計算したポリンジャーバンドを確認した後はローソク足、出来高と合わせて表示する
apd = mpf.make_addplot(df[["bb_up","bb_mid","bb_low"]])
mpf.plot(df, type="candle", addplot=apd, volume=True)
ポリンジャーバンドとローソク足によると、株価の推移はバンド上部とミッドバンドの間で変動している場合が多いといえる。
ポリンジャーバンドを表示することにより、株価の方向性と変動範囲が確認できるため株価売買の判断の参考値として利用できる。
#より高度な分析を行うため「TA-Lib」をインストールする
!wget http://prdownloads.sourceforge.net/ta-lib/ta-lib-0.4.0-src.tar.gz
!tar -xzvf ta-lib-0.4.0-src.tar.gz
!cd ta-lib && ./configure --prefix=/usr && make && make install
!pip install Ta-Lib
#株価を売買すべき転換点「売買シグナル」を利用したテクニカル指標の一つである「MACD」を計算する
import talib as ta
df = get_stock_data(2502) #アサヒGHD(2502)の株価を取得
#終値からMACDを計算
close = df["Close"]
macd, macdsignal,_ = ta.MACD(close, fastperiod=12, slowperiod=26, signalperiod=9)
df["macd"] = macd
df["macd_signal"] = macdsignal
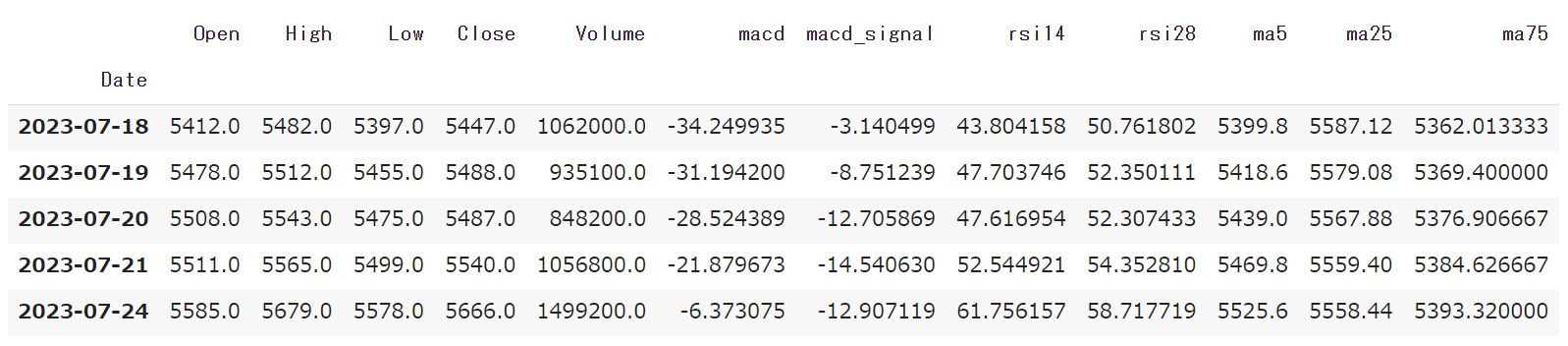
df.tail()
#計算したMACDをmpfinanceで可視化する。直近100日分のMACDをローソク足、出来高とともに表示する
import mplfinance as mpf
mdf = df.tail(100) #直近100日分のデータ
apd = [
mpf.make_addplot(mdf["macd"], panel = 2, color = "red"), #パネル2番地に赤で描画
mpf.make_addplot(mdf["macd_signal"], panel = 2, color = "blue"),
]
mpf.plot(mdf, type ="candle", volume = True, addplot = apd)
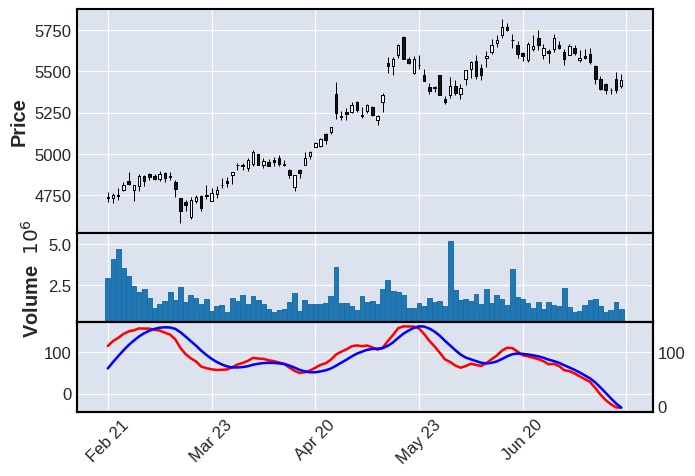
次に相場の強弱に注目したテクニカル指標で株価を分析する。ここでは「RSI」(相対力指数)を用いて、一定の日数で相場の強弱という売られすぎ/買われすぎという判断を0-100の数値で表す。
(※例えば買いが続いていてそろそろ売られるのではないか(買われすぎ)という時期が近づくとRSIの数値は100に近くなり、逆に売りが続いている(売られすぎ)という時期が近づくとRSIの数値は0に近くなる)
import talib as ta
rsi14 = ta.RSI(close, timeperiod=14)
rsi28 = ta.RSI(close, timeperiod=28)
df["rsi14"],df["rsi28"] = rsi14,rsi28
mdf = df.tail(100)
apd = [
mpf.make_addplot(mdf["rsi14"],panel=2, color="red"),
mpf.make_addplot(mdf["rsi28"],panel=2, color="blue")
]
mpf.plot(mdf,type="candle", volume=True, addplot=apd)
上段で表示した移動平均線はmplfinanceによる表示だったため、指定した日数に満たない線が表示できていなかった。
ここではTa-Libを利用して移動平均を計算し、過不足なく移動平均線を表示できるか試す。
ma5, ma25, ma75 = ta.SMA(close, timeperiod=5), ta.SMA(close, timeperiod=25), ta.SMA(close, timeperiod=75)
df["ma5"],df["ma25"],df["ma75"] = ma5,ma25,ma75
mdf = df.tail(200)
apd = [
mpf.make_addplot(mdf["ma5"],panel=0, color="blue"),
mpf.make_addplot(mdf["ma25"],panel=0, color="purple"),
mpf.make_addplot(mdf["ma75"],panel=0, color="yellow"),
]
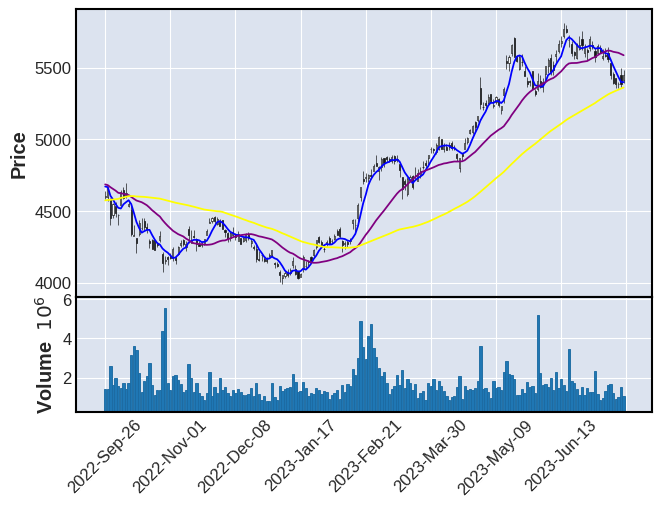
mpf.plot(mdf,type="candle", volume=True, addplot=apd)
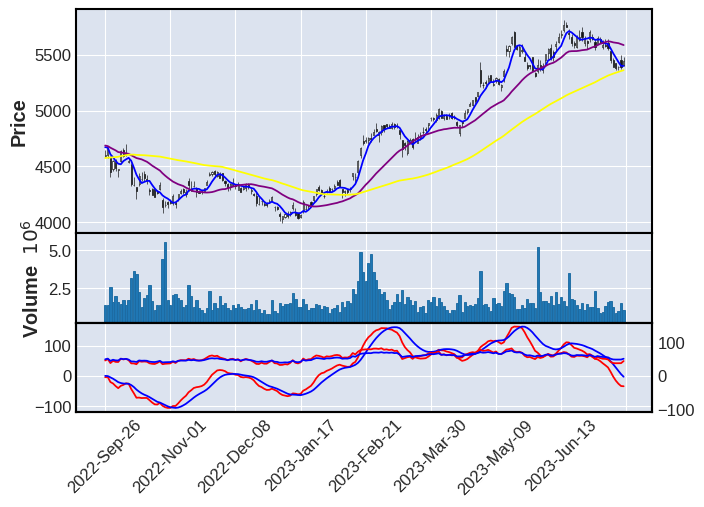
これまでに計算した移動平均、MACD、RSIを1つのグラフに表示する
MACDとRSIはY軸の値が異なるため領域をpanelプロパティで分けることで移動平均線とともに一つのグラフで表示する
このようにグラフから株価の転換点と方向性を見出す(データから洞察を得る)ことによって株価の変化に着目した分析ができた
mdf = df.tail(200)
apd = [
mpf.make_addplot(mdf["ma5"],panel=0, color="blue"),
mpf.make_addplot(mdf["ma25"],panel=0, color="purple"),
mpf.make_addplot(mdf["ma75"],panel=0, color="yellow"),
mpf.make_addplot(mdf["macd"],panel=2, color="red"),
mpf.make_addplot(mdf["macd_signal"],panel=2, color="blue"),
mpf.make_addplot(mdf["rsi14"],panel=2, color="red"),
mpf.make_addplot(mdf["rsi28"],panel=2, color="blue")
]
mpf.plot(mdf, type="candle", volume=True, addplot=apd)
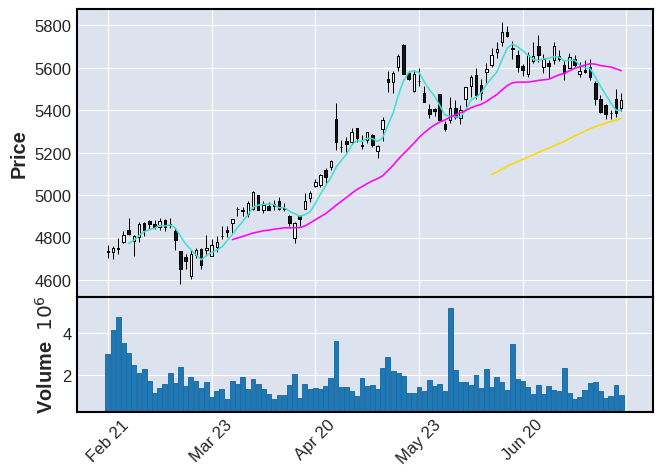
ここまで株価データを可視化した結果、線が重なったタイミングで株価が上がる/下がるという方向性がわかった。ここからはここまで確認してきた株価の転換点についてさらに深掘りすべく、株価が上昇に転じるシグナル(ゴールデンクロス)と株価が減少に転じるシグナル(デットクロス)を可視化する
import talib as ta
close = df["Close"]
ma5,ma25 = ta.SMA(close, timeperiod=5), ta.SMA(close, timeperiod=25)
df["ma5"], df["ma25"] = ma5, ma25
df.tail()
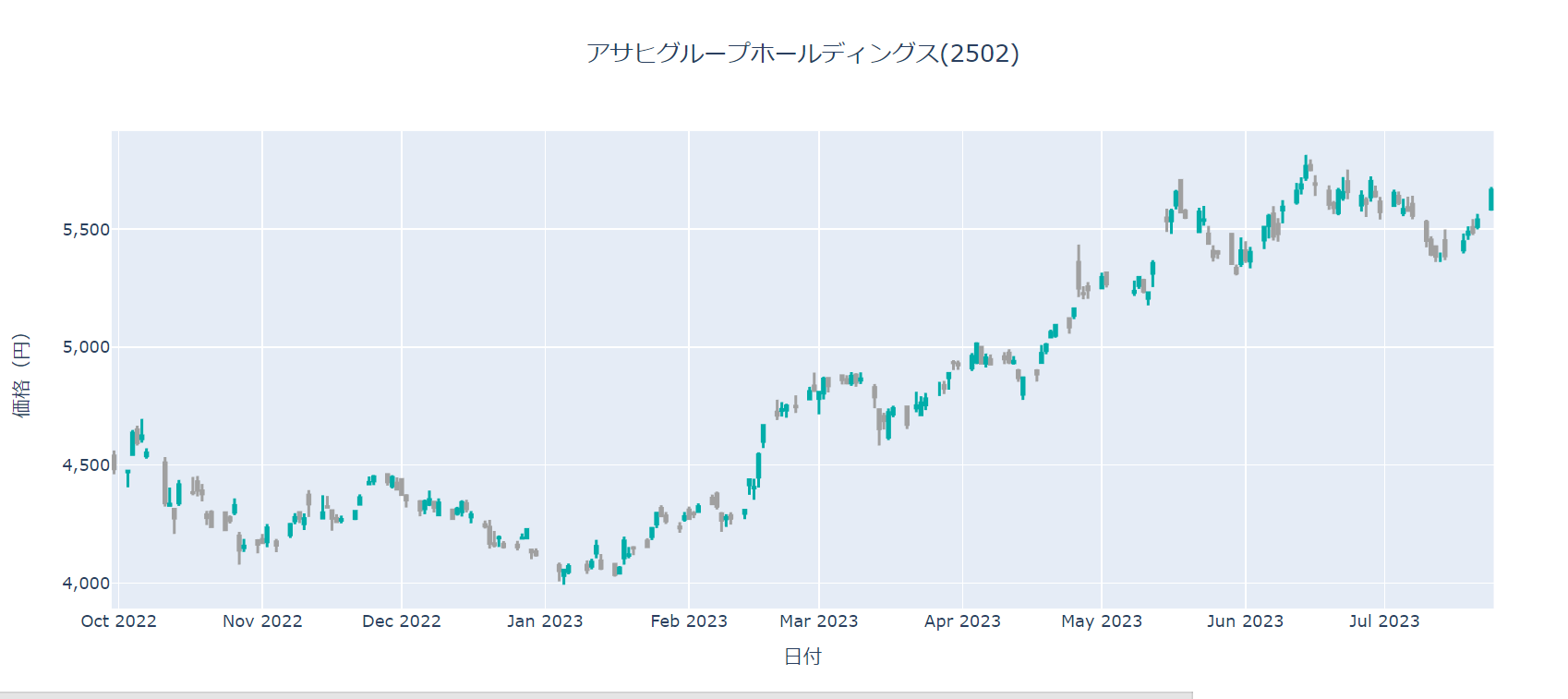
#plotlyを利用して200日分のローソク足チャートを表示してみる。plotlyでグラフを表示する際にはレイアウトをハッシュで、表示するデータを配列で定義する
import plotly.graph_objs as go
df = df.tail(200)
layout = {
"title" : {"text":"アサヒグループホールディングス(2502)","x":0.5},
"xaxis" : {"title":"日付", "rangeslider":{"visible":False}},
"yaxis" : {"title":"価格(円)","side":"left","tickformat":","
},
"plot_bgcolor":"light blue"
}
data = [
go.Candlestick(x=df.index, open=df["Open"], high=df["High"],
low=df["Low"], close=df["Close"],
increasing_line_color="#00ada9",decreasing_line_color="#a0a0a0")
]
#データの配列を定義したものが正しく設定されているか確認するため表示する
fig = go.Figure(layout = go.Layout(layout), data = data)
fig.show()
データフレームからゴールデンクロスとデッドクロスを表示するために必要な作業を割り出す。
ゴールデンクロス(移動平均線の短期線が長期線を下から上に抜くこと)とデッドクロス(短期線が長期線を上からの下に抜くこと)が起きるのは一日なので、グラフ上には点として表示する。
ゴールデンクロスの発生日には5日移動平均の値、デッドクロスの美に発生日に25日移動平均の値をデータとして持つ必要がある。
この処理は以下の3つに分けて考えることができる
1.5日移動平均と25日移動平均の値を比較
2.比較した結果が入れ替わった日がゴールデンクロスまたはデッドクロスの発生日
3.ゴールデンクロスの発生日に5日移動平均の値、デッドクロスの発生日に25日移動平均の値を保存
まず1について、5日移動平均と25日移動平均を比較して5日>25日ならTrue、5日<25日ならFalseというシリーズを作成する
import numpy as np
ma5, ma25 = df["ma5"], df["ma25"]
cross = ma5 > ma25
次に、2について、前項で作成したシリーズにおいてゴールデンクロスの発生日、デッドクロスの発生日を干出する処理を作成する
cross_shift = cross.shift(1)
temp_gc = (cross != cross_shift)&(cross == True)
temp_dc = (cross !=cross_shift)&(cross == False)
最後に3について、ゴールデンクロスの発生日に5日の移動平均線、デッドクロスの発生日に25日の移動平均線を記載する
gc = [m if g == True else np.nan for g, m in zip(temp_gc,ma5)]
dc = [m if d == True else np.nan for d, m in zip(temp_dc,ma25)]
df["gc"], df["dc"] = gc, dc
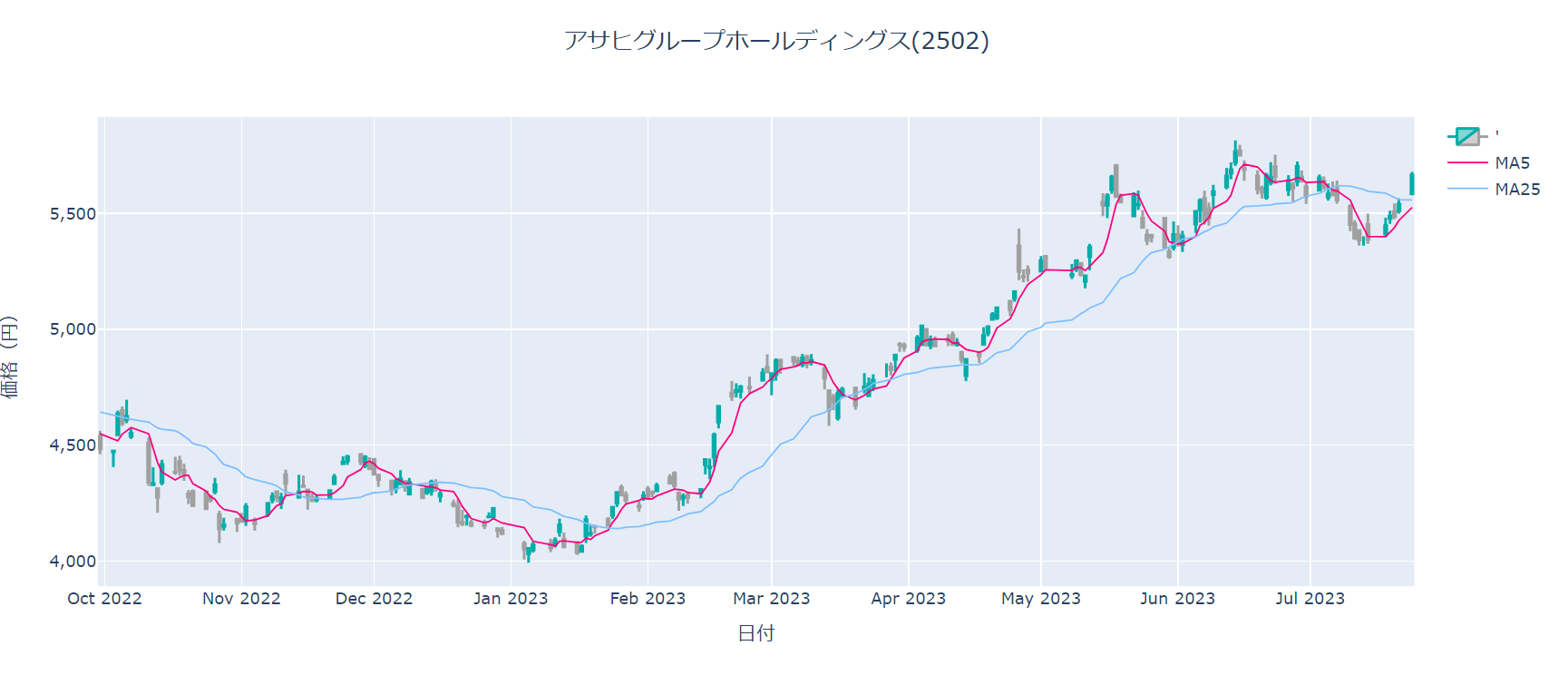
前項までで作成したカラムを利用し、移動平均線、ゴールデンクロス、デッドクロスをまとめてチャートに表示する
#まずは移動平均線を表示する
data = [
go.Candlestick(x = df.index, open=df["Open"], high=df["High"], low=df["Low"], close=df["Close"],
name="'", increasing_line_color="#00ada9", zdecreasing_line_color="#a0a0a0"),
go.Scatter(x=df.index, y=df["ma5"], name= "MA5", line=dict(color="#ff007F", width=1.2)),
go.Scatter(x=df.index, y=df["ma25"], name= "MA25", line=dict(color="#7fbfff", width=1.2))
]
fig = go.Figure(data = data, layout = go.Layout(layout))
fig.show()
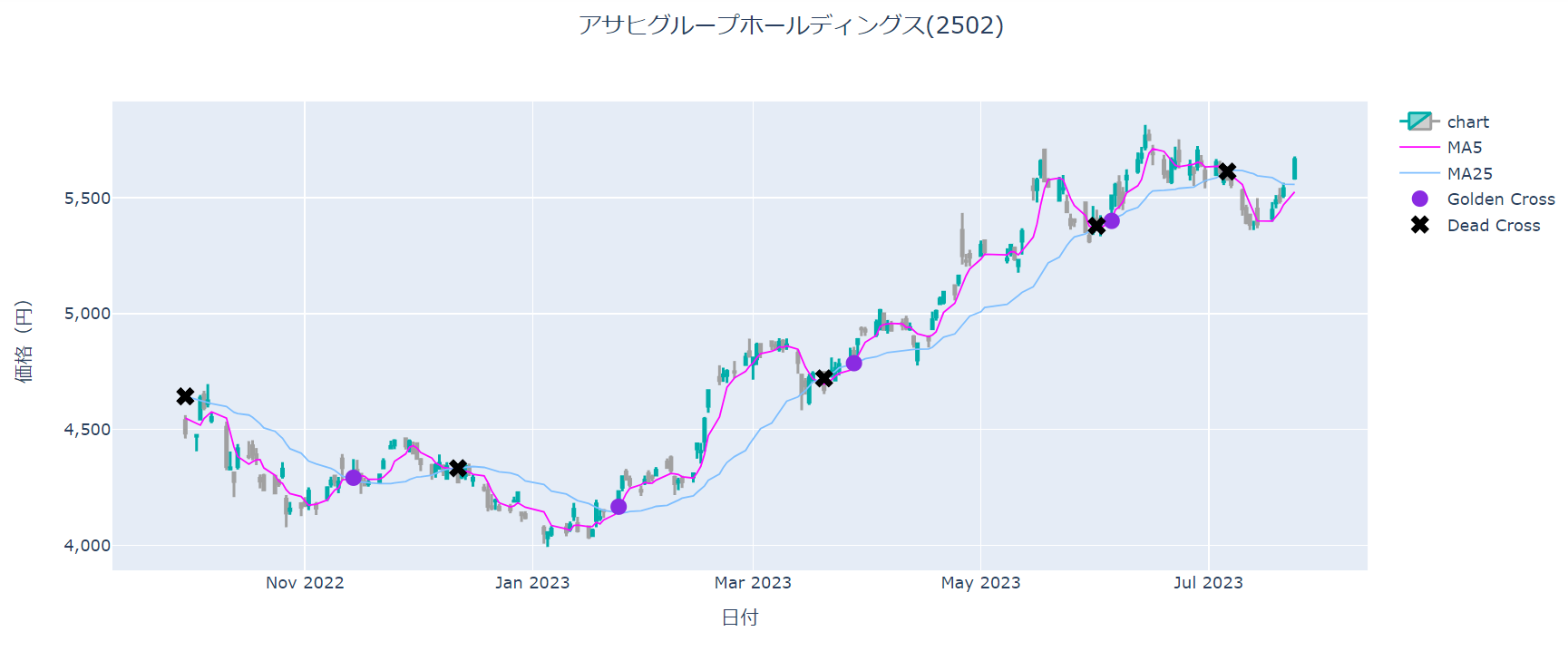
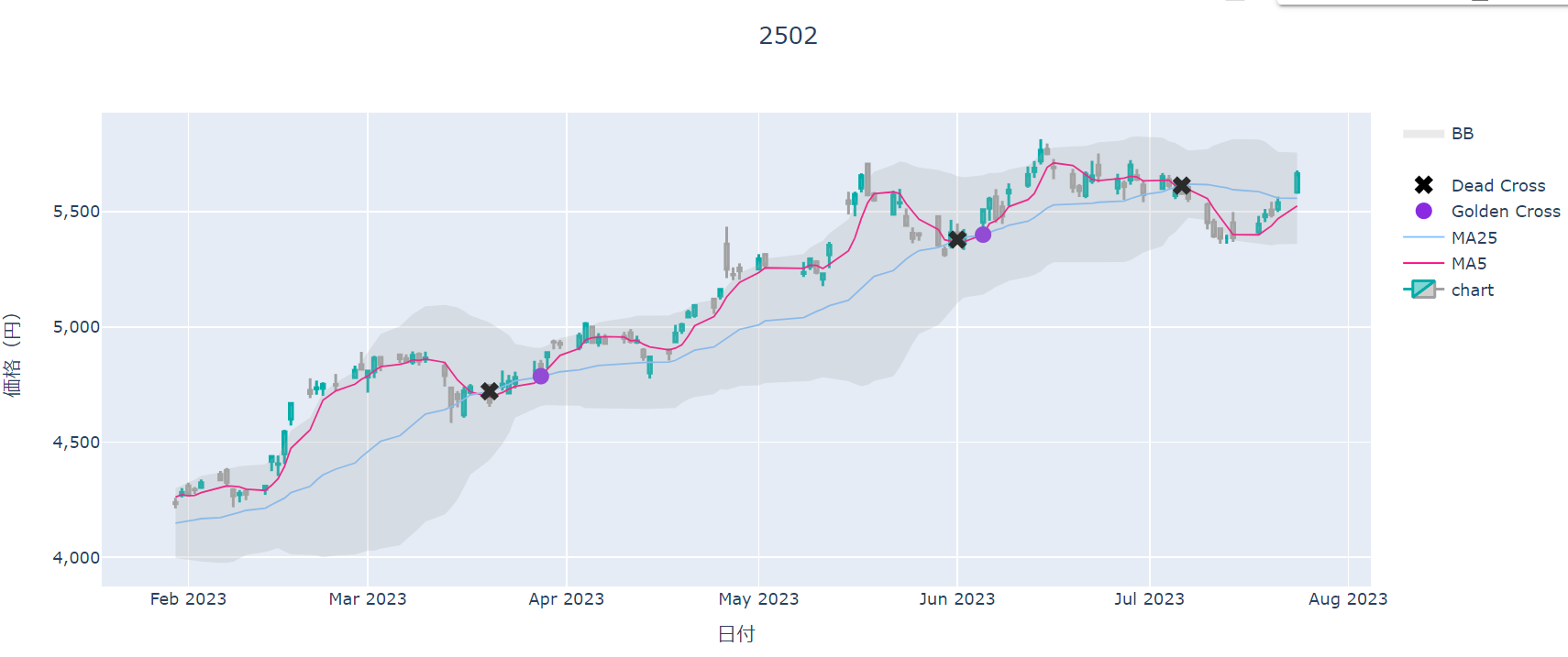
#移動平均線に加えて、ゴールデンクロスとデッドクロスを表示する
それぞれは線ではなくグラフ上のマーカとして表示する
data = [
go.Candlestick(name="chart", x = df.index, open=df["Open"], high=df["High"], low=df["Low"], close=df["Close"], increasing_line_color= "#00ada9", decreasing_line_color="#a0a0a0"),
go.Scatter(x=df.index, y=df["ma5"], name="MA5", line=dict(color="#ff07ff",width=1.2)),
go.Scatter(x=df.index, y=df["ma25"], name="MA25", line=dict(color="#7fbfff",width=1.2)),
go.Scatter(x=df.index, y=df["gc"], name="Golden Cross", mode="markers",marker=dict(size = 12,color="blueviolet")),
go.Scatter(x=df.index, y=df["dc"], name="Dead Cross", mode="markers", marker=dict(size =12, color="black", symbol="x"))
]
fig = go.Figure(data = data, layout = go.Layout(layout))
fig.show()
これまでに算出したオシレーターを一つのグラフで表示する
#まずはアサヒグループホールディングスの株価の取得とボリンジャーバンドの計算をする
!pip install pyti
from pyti.bollinger_bands import upper_bollinger_band as bb_up
from pyti.bollinger_bands import middle_bollinger_band as bb_mid
from pyti.bollinger_bands import lower_bollinger_band as bb_low
df = get_stock_data(2502)
data = df["Close"].tolist()
period = 25
bb_up, bb_mid, bb_low = bb_up(data, period), bb_mid(data, period),bb_low(data, period)
df["bb_up"],df["bb_mid"],df["bb_low"] = bb_up, bb_mid, bb_low
#次にオシレーターと移動平均の計算を行う
import talib as ta
close = df["Close"]
macd, macdsignal,_= ta.MACD(close, fastperiod=12, slowperiod=26, signalperiod=9)
df["macd"], df["rsi28"] = rsi14, rsi28
rsi14, rsi28 = ta.RSI(close, timeperiod=14), ta.RSI(close, timeperiod=28)
df["rsi14"],df["rsi28"] = rsi14, rsi28
ma5, ma25, ma75 = ta.SMA(close, timeperiod=5), ta.SMA(close, timeperiod=25),ta.SMA(close, timeperiod=75)
df["ma5"],df["ma25"],df["ma75"] = ma5, ma25, ma75
#ゴールデンクロスとデッドクロスを算出する
import numpy as np
ma5, ma25 = df["ma5"], df["ma25"]
cross = ma5 > ma25
cross_shift = cross.shift(1)
temp_gc = (cross != cross_shift) & (cross == True)
temp_dc = (cross != cross_shift) & (cross == False)
gc = [m if g == True else np.nan for g, m in zip(temp_gc, ma5)]
dc = [m if d == True else np.nan for d, m in zip(temp_dc, ma25)]
df["gc"],df["dc"] = gc, dc
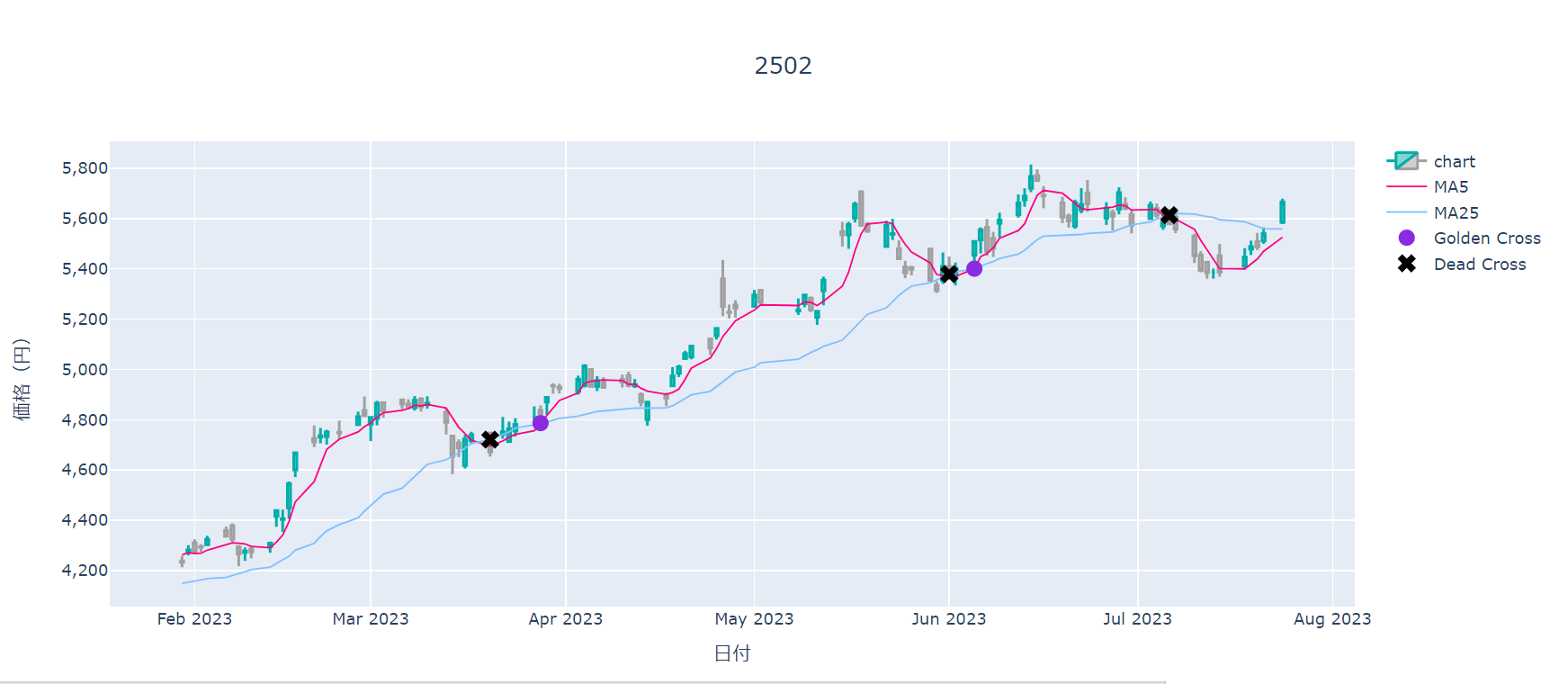
#計算結果を確認するために、グラフを描画させて直近120日分のデータを表示する(上段で作成したグラフと同じもの)
import plotly.graph_objs as go
pdf = df.tail(120)
layout = {
"title" : {"text": "2502", "x":0.5},
"xaxis" : {"title" : "日付","rangeslider":{"visible": False}},
"yaxis" : {"title" : "価格(円)", "tickformat": ","},
"plot_bgcolor" : "light blue"
}
data =[
go.Candlestick(name="chart", x = pdf.index, open=pdf["Open"], high=pdf["High"],
low=pdf["Low"], close=pdf["Close"],
increasing_line_color="#00ada9", decreasing_line_color="#a0a0a0"),
go.Scatter(x = pdf.index, y=pdf["ma5"], name="MA5", line=dict(color="#ff007f", width=1.2)),
go.Scatter(x=pdf.index, y=pdf["ma25"], name="MA25", line=dict(color="#7fbfff",width=1.2)),
go.Scatter(x=pdf.index, y=pdf["gc"], name="Golden Cross", mode="markers",marker=dict(size = 12,color="blueviolet")),
go.Scatter(x=pdf.index, y=pdf["dc"], name="Dead Cross", mode="markers", marker=dict(size =12, color="black", symbol="x"))
]
fig = go.Figure(data = data, layout = go.Layout(layout))
fig.show()
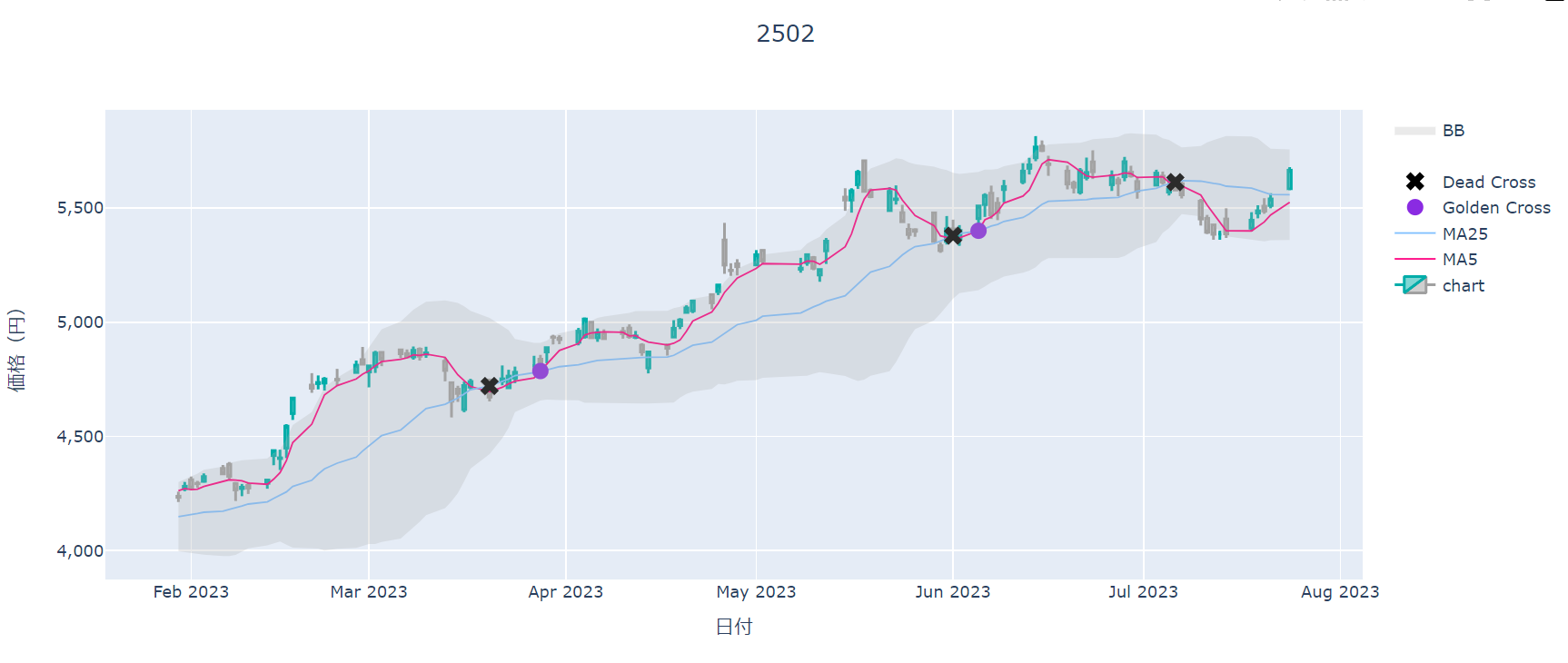
#ポリンジャーバンドの表示とデータ調整を行う
data = [
go.Candlestick(name="chart", x = pdf.index, open=pdf["Open"], high=pdf["High"],
low=pdf["Low"], close=pdf["Close"],
increasing_line_color="#00ada9", decreasing_line_color="#a0a0a0"),
go.Scatter(x = pdf.index, y=pdf["ma5"], name="MA5", line=dict(color="#ff007f", width=1.2)),
go.Scatter(x = pdf.index, y=pdf["ma25"], name="MA25", line=dict(color="#7fbfff",width=1.2)),
go.Scatter(x = pdf.index, y=pdf["gc"], name="Golden Cross", mode="markers",marker=dict(size = 12,color="blueviolet")),
go.Scatter(x = pdf.index, y=pdf["dc"], name="Dead Cross", mode="markers", marker=dict(size =12, color="black", symbol="x")),
go.Scatter(x = pdf.index, y=pdf["bb_up"], name="", line=dict(width=0)),
go.Scatter(x = pdf.index, y=pdf["bb_low"], name= "BB", line=dict(width=0),
fill = "tonexty", fillcolor = "rgba(170,170,170,0.25)"),
]
fig = go.Figure(data = data, layout = go.Layout(layout))
fig.show()
株価のindexはDataTime型であり、グラフに表示する際には株価データの存在しない営業日以外の土日祝日もデータがあるものと自動的に解釈されるので、X軸が開いてしまっている部分がある。
これをX軸の空きをなくす処理を作成してX軸に空きがないようにします。まずインデックスをDataTime型でない数値の連番に変更する。
df.reset_index(inplace=True)
#3日に1日の日付を取り出す
days_list = [df.index[idx:idx + 3] for idx in range(0,len(df.index), 3)]
dates = [df["Date"][r[0]] for r in days_list]
#X軸を更新
fig["layout"].update({
"xaxis" : {
"showgrid" : True,
"tickvals" : np.arange(0, df.index[-1],3),
"ticktext" : [x.strftime("%m/%d") for x in dates],
}
})
fig = go.Figure(data = data, layout = go.Layout(layout))
fig.show()
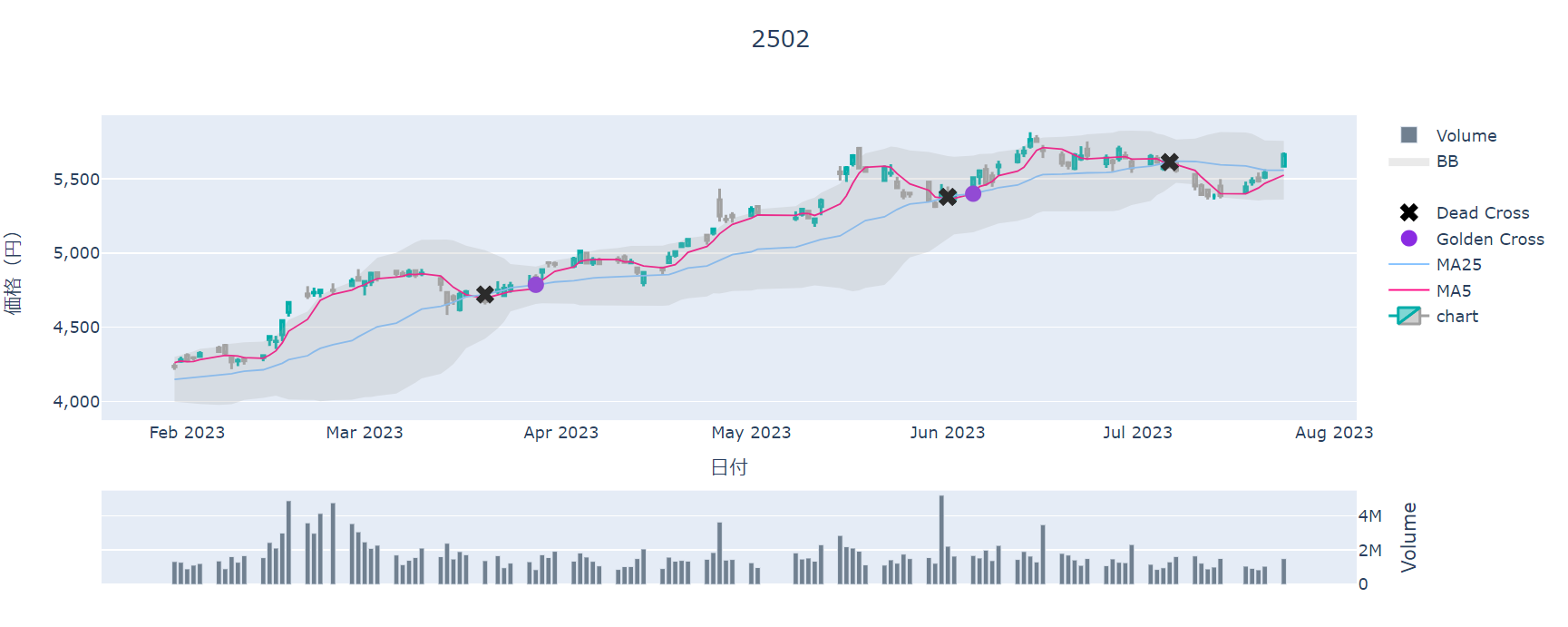
出来高とオシレーターの表示
日付の調整後、出来高とオシレーターを表示する。表示する領域を分割してすべてを1枚のグラフで表示する
#まずは領域を3つに定義する
layout = {
"title" : {"text" : "2502", "x" :0.5},
"xaxis" : {"title" : "日付", "rangeslider": {"visible" : False}},
"yaxis1" : {"domain" :[0.35,1], "title" : "価格(円)", "tickformat" :","
},
"yaxis2" : {"domain" :[0.2,0.35]},
"yaxis3" : {"domain" :[0.0,0.2], "title": "Volume", "side" : "right"},
"plot_bgcolor" : "light blue"
}
#作成した領域でうえから株価のグラフ、日付、出来高の順に表示する
data = [
#ローソク足
go.Candlestick(yaxis="y1", name="chart", x = pdf.index, open=pdf["Open"], high=pdf["High"], low=pdf["Low"], close=pdf["Close"],
increasing_line_color="#00ada9", decreasing_line_color="#a0a0a0"),
#5日移動平均線
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["ma5"], name = "MA5", line=dict(color="#ff007f", width=1.2)),
#25日移動平均線
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["ma25"], name = "MA25", line=dict(color="#7fbfff", width=1.2)),
#ゴールデンクロス
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["gc"], name = "Golden Cross", mode = "markers", marker=dict(size = 12, color = "blueviolet")),
#デッドクロス
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["dc"], name = "Dead Cross", mode = "markers", marker=dict(size = 12, color = "black", symbol = "x")),
#ボリンジャーバンド上限
go.Scatter(x = pdf.index, y=pdf["bb_up"], name="", line=dict(width=0)),
#ボリンジャーバンド下限
go.Scatter(yaxis="y1", x = pdf.index, y=pdf["bb_low"], name= "BB", line=dict(width=0),
fill = "tonexty", fillcolor = "rgba(170,170,170,0.25)"),
#出来高
go.Bar(yaxis="y3", x = pdf.index, y=pdf["Volume"], name="Volume", marker=dict(color="slategray"))
]
fig = go.Figure(data = data, layout = go.Layout(layout))
fig.show()
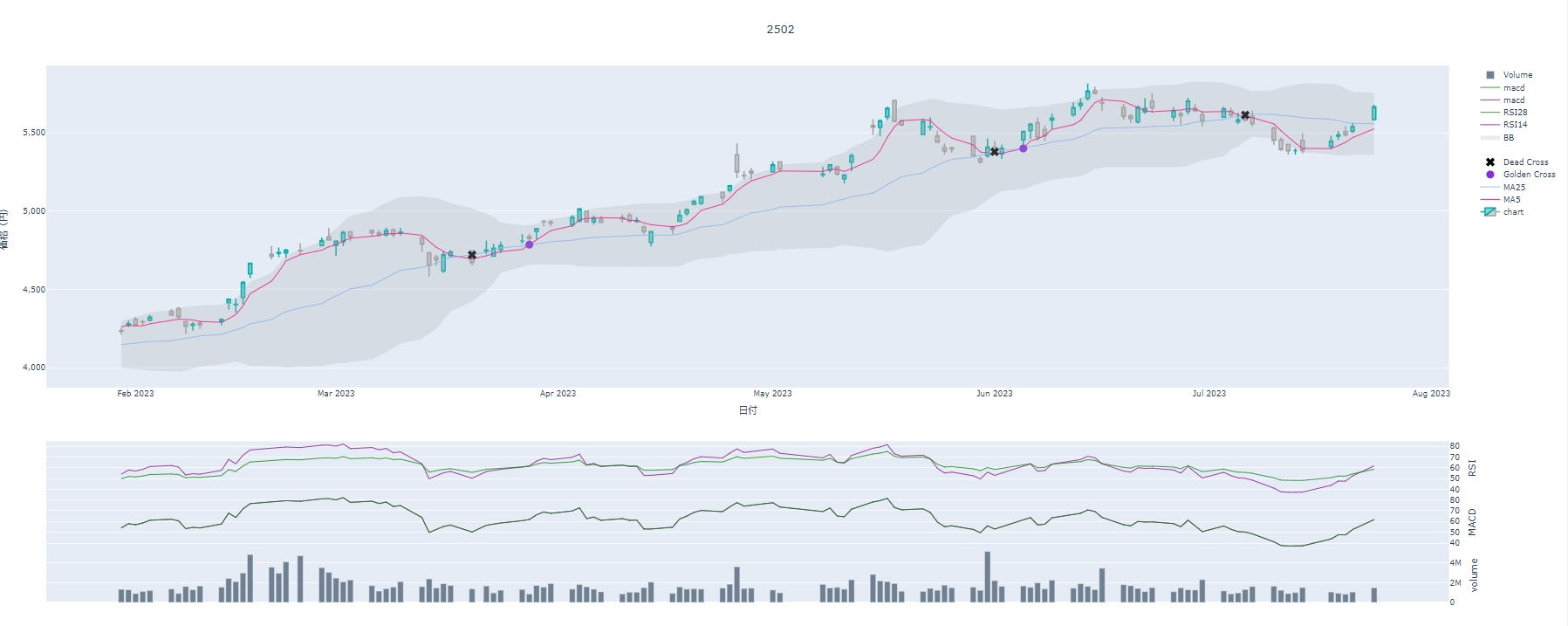
MACD,RSIを表示する
layout = { "height" : 1000,
"title" : {"text" : "2502", "x" : 0.5},
"xaxis" : {"title" : "日付", "rangeslider" :{"visible" : False}},
"yaxis1" : {"domain" : [0.40,1], "title": "価格(円)", "side" : "left",
"tickformat" : ","},
"yaxis2" : {"domain" : [0.30,0.40], "title": "", "side" : "right"},
"yaxis3" : {"domain" : [0.20,0.30], "title" : "RSI", "side" : "right"},
"yaxis4" : {"domain" : [0.10,0.20], "title" : "MACD", "side" : "right"},
"yaxis5" : {"domain" : [0.0,0.10], "title" : "volume", "side" : "right"},
"plot_bgcolor" : "light blue"
}
data = [
#ローソク足
go.Candlestick(yaxis="y1", name="chart", x = pdf.index, open=pdf["Open"], high=pdf["High"], low=pdf["Low"], close=pdf["Close"],
increasing_line_color="#00ada9", decreasing_line_color="#a0a0a0"),
#5日移動平均線
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["ma5"], name = "MA5", line=dict(color="#ff007f", width=1.2)),
#25日移動平均線
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["ma25"], name = "MA25", line=dict(color="#7fbfff", width=1.2)),
#ゴールデンクロス
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["gc"], name = "Golden Cross", mode = "markers", marker=dict(size = 12, color = "blueviolet")),
#デッドクロス
go.Scatter(yaxis="y1", x =pdf.index, y=pdf["dc"], name = "Dead Cross", mode = "markers", marker=dict(size = 12, color = "black", symbol = "x")),
#ボリンジャーバンド上限
go.Scatter(x = pdf.index, y=pdf["bb_up"], name="", line=dict(width=0)),
#ボリンジャーバンド下限
go.Scatter(yaxis="y1", x = pdf.index, y=pdf["bb_low"], name= "BB", line=dict(width=0),
fill = "tonexty", fillcolor = "rgba(170,170,170,0.25)"),
#短期RSI
go.Scatter(yaxis="y3", x=pdf.index ,y=pdf["rsi14"], name="RSI14", line=dict(color="purple" ,width=1)),
#長期RSI
go.Scatter(yaxis="y3", x=pdf.index ,y=pdf["rsi28"], name="RSI28", line=dict(color="green" ,width=1)),
#MACD
go.Scatter(yaxis="y4", x=pdf.index ,y=pdf["macd"], name="macd", line=dict(color="purple" ,width=1)),
#MACDシグナル
go.Scatter(yaxis="y4", x=pdf.index ,y=pdf["macd"], name="macd", line=dict(color="green" ,width=1)),
#出来高
go.Bar(yaxis="y5", x = pdf.index, y=pdf["Volume"], name="Volume",marker=dict(color="slategray"))
]
fig = go.Figure(data = data, layout = go.Layout(layout))
fig.show()
4.株価予測
Meta(旧Facebook)が公開している時系列予測ライブラリ「Prophet」を利用すると、過去の株価データから今後の株価を予想できる。ただし、過去の株価だけで将来の株価をすべて予想できるとは限らない。
!pip install prophet
df = get_stock_data(2502)
df["ds"] = df.index
df = df.rename(columns={"Close": "y"})
#今後の株価を予測する
from prophet import Prophet
m = Prophet()
m.fit(df)
future = m.make_future_dataframe(periods=365)
forecast = m.predict(future)
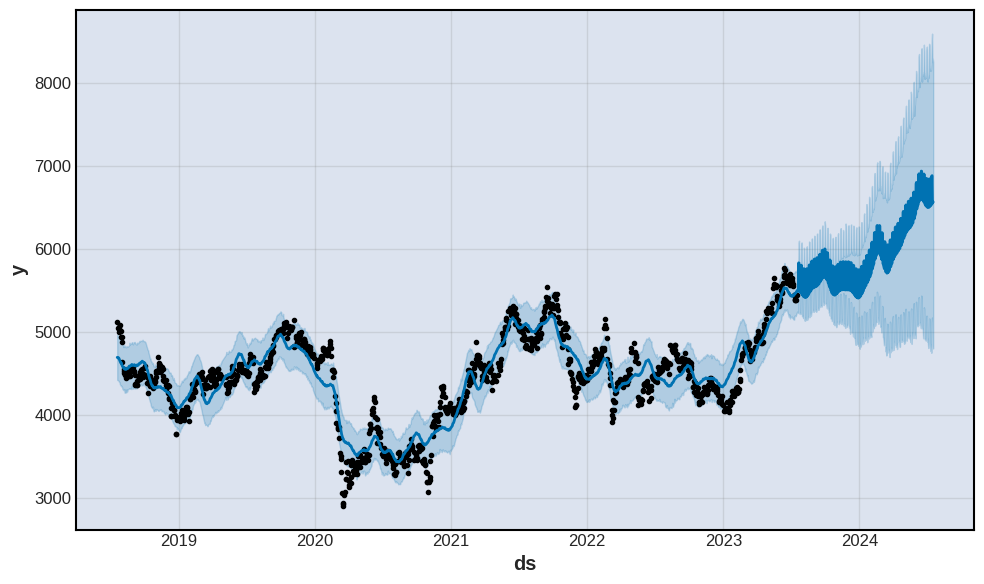
fig = m.plot(forecast)
予測の結果、アサヒグループホールディングス(2502)の株価はコロナ禍の影響による2020年ごろの大幅な株価下落から段階的に回復してきていており、2023年下期以降も上昇傾向を維持し、2024年下期ごろには6,000円から7,000円程度で推移する見込みであると想定する。
ここからは機械学習のLSTMを使用して予測を行い、結果を確認する。
#モジュールインポート
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader.data as pdr
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.preprocessing import StandardScaler
plt.style.use('ggplot')
#window_sizeに分けて時系列データのデータセットを作成
def apply_window(data, window_size):
#データをwindow_sizeごとに分割
sequence_length = window_size
window_data = []
for index in range(len(data) - window_size):
window = data[index: index + sequence_length]
window_data.append(window)
return np.array(window_data)
#訓練データと検証データに分ける
def split_train_test(data, train_rate=0.7):
#データの古い方7割(デフォルト値0.7)を訓練用データとし、残りをテスト用データとする
row = round(train_rate * data.shape[0])
train = data[:row]
test = data[row:]
return train, test
def data_load():
#アサヒグループホールディングスの株価ファイル読み込み
df= pdr.DataReader("2502.JP","stooq")
df.reset_index(inplace= True)
#Data列を日付データとして認識
df['Date'] = pd.to_datetime(df['Date'])
#日付順に並び替え
df.sort_values(by='Date', inplace=True)
#終値を抽出
close_ts = df['Close']
close_ts = np.expand_dims(close_ts, 1)
return close_ts
def train_model(X_train, y_train, units=15):
#入力データの形式を取得
input_size = X_train.shape[1:]
#レイヤーを定義
model = keras.Sequential()
model.add(layers.LSTM(
input_shape=input_size,
units=units,
dropout = 0.1,
return_sequences=False,))
model.add(layers.Dense(units=1))
model.compile(loss='mse', optimizer='adam', metrics=['mean_squared_error'])
model.fit(X_train, y_train,
epochs=10, validation_split=0.3, verbose=2, shuffle=False)
return model
def predict(data, model):
pred = model.predict(data,verbose=0)
return pred.flatten()
#モデルに入力するデータ長
window_size = 15
#アサヒグループホールディングスの株価・終値を取得
close_ts = data_load()
#データを訓練用・学習用に分割
train, test = split_train_test(close_ts)
#データを正規化
scaler = StandardScaler()
train = scaler.fit_transform(train)
test = scaler.transform(test)
#一定の長さのデータを作る
train = apply_window(train, window_size+1)
test = apply_window(test, window_size+1)
#訓練用の入力データ
X_train = train[:, :-1]
# 訓練用の正解ラベル
y_train = train[:, -1]
#テスト用の入力データ
X_test = test[:, :-1]
#テスト用の正解ラベル
y_test = test[:, -1]
#学習モデルを取得
model = train_model(X_train, y_train, units=15)
#検証データで予測
predicted = predict(X_test, model)
predicted = predicted.reshape([-1, predicted.shape[0]])
plt.figure(figsize=(15, 8))
plt.plot(scaler.inverse_transform(y_test),label='True Data')
plt.plot(scaler.inverse_transform(predicted).reshape([predicted.shape[1]]),label='Prediction')
plt.legend()
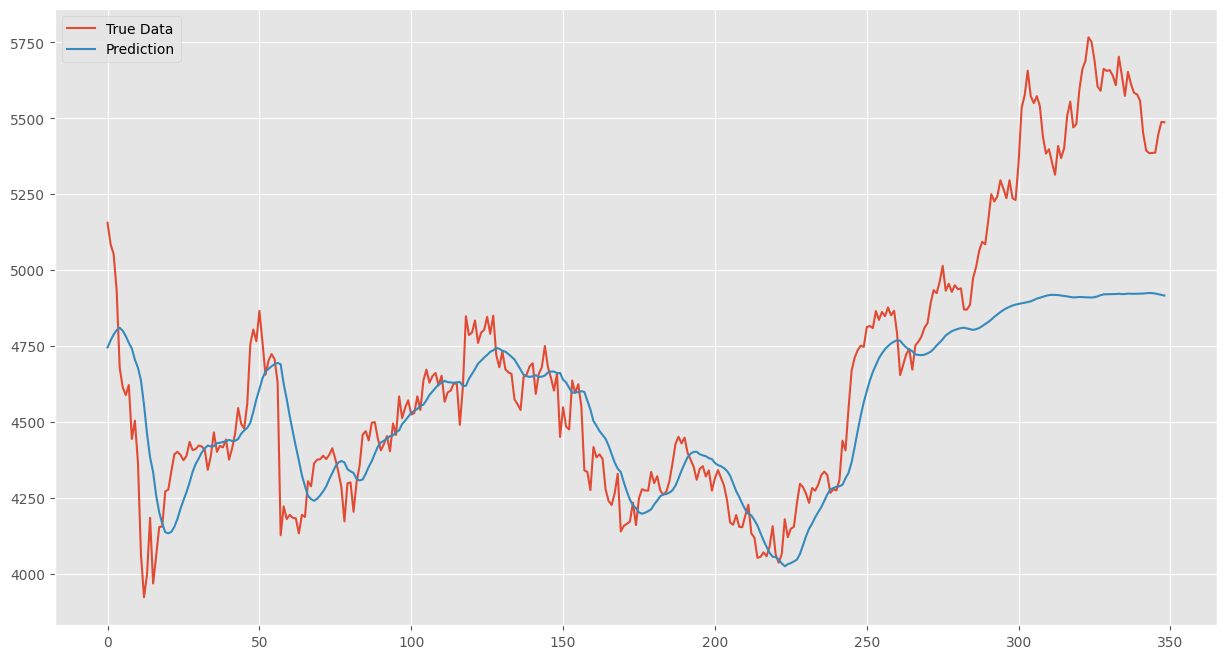
plt.show()
上記の予測の結果を見ると、後半にかけてかなり乖離がある。
モデルの精度を上げるために学習のエポック数を増やしてみる。また、モデルのレイヤーを増やして複雑にしてみる。
#モジュールインポート
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
import pandas_datareader.data as pdr
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from sklearn.preprocessing import StandardScaler
plt.style.use('ggplot')
#window_sizeに分けて時系列データのデータセットを作成
def apply_window(data, window_size):
# データをwindow_sizeごとに分割
sequence_length = window_size
window_data = []
for index in range(len(data) - window_size):
window = data[index: index + sequence_length]
window_data.append(window)
return np.array(window_data)
#訓練データと検証データに分ける
def split_train_test(data, train_rate=0.7):
# データの古い方7割(デフォルト値0.7)を訓練用データとし、 残りをテスト用データとする
row = round(train_rate * data.shape[0])
train = data[:row]
test = data[row:]
return train, test
def data_load():
#アサヒグループホールディングスの株価ファイル読み込み
df= pdr.DataReader("2502.JP","stooq")
df.reset_index(inplace= True)
#Data列を日付データとして認識
df['Date'] = pd.to_datetime(df['Date'])
#日付順に並び替え
df.sort_values(by='Date', inplace=True)
#終値を抽出
close_ts = df['Close']
close_ts = np.expand_dims(close_ts, 1)
return close_ts
def train_model(X_train, y_train, units=32):
#入力データの形式を取得
input_size = X_train.shape[1:]
#レイヤーを定義
model = keras.Sequential()
model.add(layers.LSTM(
input_shape=input_size,
units=units,
return_sequences=True))
model.add(layers.LSTM(
units=units,
dropout = 0.2,
return_sequences=False))
model.add(layers.Dense(units=1))
model.compile(loss='mse', optimizer='adam', metrics=['mean_squared_error'])
model.fit(X_train, y_train, batch_size=32,
epochs=200, validation_split=0.3, verbose=2, shuffle=False)
return model
def predict(data, model):
pred = model.predict(data,verbose=0)
return pred.flatten()
#モデルに入力するデータ長
window_size = 15
#アサヒグループホールディングスの株価・終値を取得
close_ts = data_load()
#データを訓練用・学習用に分割
train, test = split_train_test(close_ts)
#データを正規化
scaler = StandardScaler()
train = scaler.fit_transform(train)
test = scaler.transform(test)
#一定の長さのデータを作る
train = apply_window(train, window_size+1)
test = apply_window(test, window_size+1)
#訓練用の入力データ
X_train = train[:, :-1]
#訓練用の正解ラベル
y_train = train[:, -1]
#テスト用の入力データ
X_test = test[:, :-1]
#テスト用の正解ラベル
y_test = test[:, -1]
#学習モデルを取得
model = train_model(X_train, y_train, units=15)
#検証データで予測
predicted = predict(X_test, model)
predicted = predicted.reshape([-1, predicted.shape[0]])
plt.figure(figsize=(15, 8))
plt.plot(scaler.inverse_transform(y_test),label='True Data')
plt.plot(scaler.inverse_transform(predicted).reshape([predicted.shape[1]]),label='Prediction')
plt.legend()
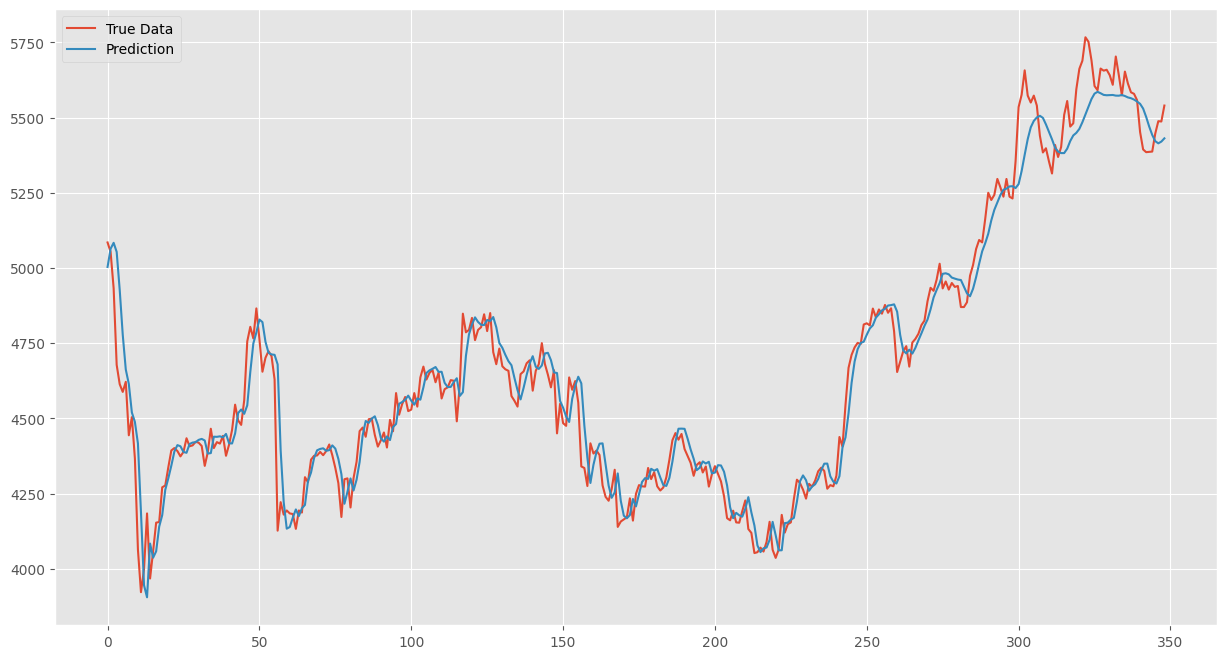
plt.show()
上記のグラフでは横軸が株価データの数になっており、「Prophet」の予測との比較が難しい。グラフの軸をそろえるために横軸を時間に変更する(描写時の表示形式の変更)
#アサヒグループホールディングスの株価ファイル読み込み
df= pdr.DataReader("2502.JP","stooq")
df.reset_index(inplace= True)
#Data列を日付データとして認識
df['Date'] = pd.to_datetime(df['Date'])
#日付順に並び替え
df.sort_values(by='Date', inplace=True)
df.index = df["Date"]
#終値を抽出
close_ts = df['Close']
row = round(0.7 * close_ts.shape[0])
train = close_ts[:row]
test = close_ts[row:]
date = []
for t in list(test.index):
if t.strftime('%Y-%m-%d') == '2022-06-30' or t.strftime('%Y-%m-%d') == '2023-06-30':
date.append(t.strftime('%Y'))
else:
date.append(None)
plt.figure(figsize=(30, 8))
plt.xticks(list(range(365)), date)
plt.plot(scaler.inverse_transform(y_test),label='True Data')
plt.plot(scaler.inverse_transform(predicted).reshape([predicted.shape[1]]),label='Prediction')
plt.legend()
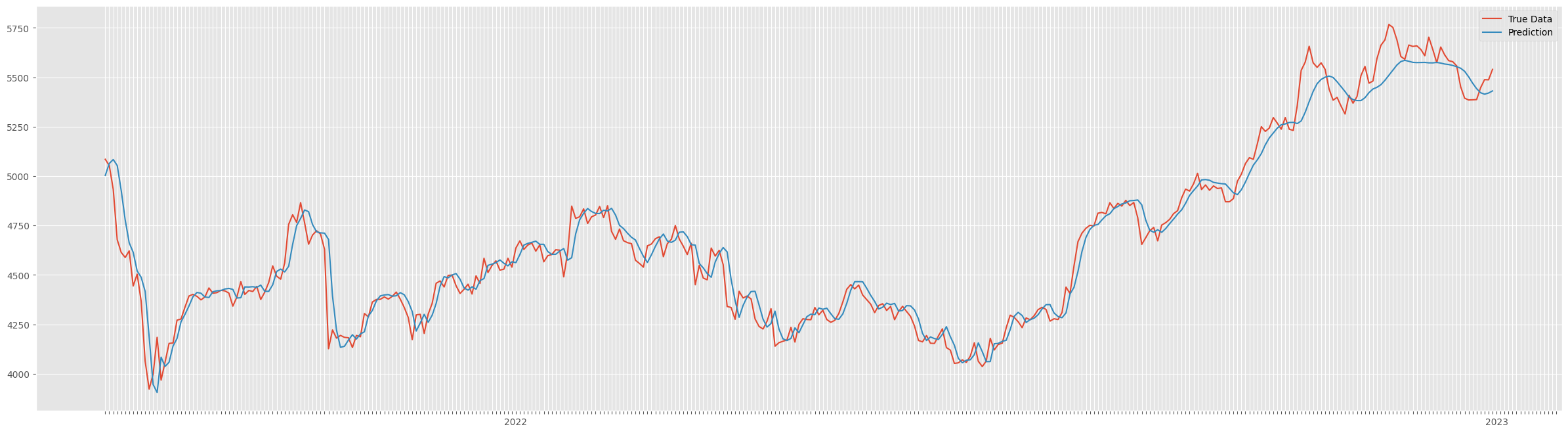
plt.show()
おわりに
今回アイデミーでの学習を通じて、プログラミングは実際に手を動かしながら学ぶことによって、理解が深まり、また正しいコードがかけたときの達成感・快感がとても心地よいものだと感じました。
また私の場合は本業とのバランスが取れず数か月空いてしまった時期がありましたが、思い出しのために一度習ったことを手を動かしながら復習する方法が一番よいと感じました。そして上達のためには「迷ったら5分以内に検索・質問する!(チューターの方から教わったことです)」で忙しい中での学習を最後までやりきることができました。
特に質問することにおいて、私の場合はまずweb検索でエラーメッセージと調べ(ここで50%は解決できるイメージ)ChatGPTによるチャットボットで質問をし、それでも解決できない場合はチューターにチャット・カウンセリングで質問という流れで解消していました。実際は、自分の知識のストックが不十分であることもあり、webで調べて解決できないものはChatGPTの回答を見てもよく理解できず、チューターさん頼みになっていました。ChatGPTをいかにうまく使うか(これはプログラミングに限らずですが)も今後の課題であると感じました。
(補足)Aidemy・教育訓練給付について
私がデータ分析の学習を思い立ってから数日のうちにいくつかのプログラミング講座を検討し、カウンセリングを受けました。その中でも今回利用したAidemyは講師のフォローが手厚そうな印象があったため受講を決めました。実際にバーチャル学習室やSlackでの質問対応、カウンセリングなど様々な方法でいつでも質問ができる環境でした。
また、今回の講座受講にあたって、経済産業省と厚生労働省が認定する講座「第四次産業革命スキル習得講座認定制度」を利用しました。要件を満たし、ハローワークにて手順を踏んで申請を行い修了した場合、受講経費の最大70%を給付金として支給されます。支援制度の充実度合いから、プログラミングを学び始めるには非常に良い環境が整っている状況だと感じます。この機会にチャレンジしてみてはいかがでしょうか。