年末にQiita初投稿します。
動機
急ですが、「多重共線性で回帰が上手くいかなくなる」みたいな説明は
よく聞くけど「じゃあ、実際に影響があるのか?」を一緒に検証して
くれてることは少ない気がします。
そういうわけで、回帰係数の推定精度が低くなるかテストしました。
(あと暇だった)
忙しい人のための結論ファースト
多重共線性がある場合に回帰係数の推定精度が低下することは確認できました。
絵の説明は後半に続きます。

検証方法
①推定精度の確認方法は?
正解となる回帰係数の値を用意し、推定値との比較を
おこなうことで確認します。
また、説明変数$x_i$のデータは以下の2ケースで作成します。
- 相関を持たせない
- 強相関(係数1.0)を持たせる
②どうやって回帰するか?
基礎的な手法である最小二乗法で求めます。
線形回帰のPython実装
最小二乗法を実行するために、scikit-learnのLinearRegressionを使います。
from sklearn.linear_model import LinearRegression
lr_model = LinearRegression()
lr_model.fit(X_train, Y_train)
lr_pred = lr_model.predict(X_test)
データの実装
今回、説明変数$x_i$のデータは、サンプル数×次元($N$×$M_x$)の行列を乱数で作ります。
目的変数$y_i$は1次元でもよかったですが、せっかくなので、$N$×$M_y$次元で持たせます。
このとき、説明変数は行列 $X$ 、目的変数は行列 $Y$ で表されます。
このとき、回帰係数も行列 $A$ で表すことができます。
方程式は行列を用いることで、以下の連立方程式で表現できます。
$$Y=XA$$
行列$A$はスパース(値0が含まれる)な乱数行列で作成します。
$Y$ は $Y=XA$ で算出します。
強相関の設定は、説明変数Xの次元を他の次元にコピーして行います。
つまり、相関は1.0になります。
相関係数を調整するならホワイトノイズを加えてもいいかもしれません。
検証開始
ライブラリをimportしておきます。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.datasets import make_regression
from scipy.sparse import random
import warnings
warnings.filterwarnings('ignore')
pd.set_option("display.max_rows", 20, "display.max_columns", None)
説明変数に相関がない場合の回帰
次にデータセット_ケース1を作成します。
# データセットの作成
n_samples = 100
n_features = 10
n_targets = 4
X, y = make_regression(n_samples=100, n_features=10, n_targets=4, random_state=42)
# スパース行列Aの作成
# densitiyは0.2 or 1.0
A = random(n_features, n_targets, density=1.0, format="csr", random_state=42)
# Yの計算
Y = X @ A.toarray()
# データフレームへの変換
X_df = pd.DataFrame(X, columns=[f"X{i}" for i in range(n_features)])
Y_df = pd.DataFrame(Y, columns=[f"Y{i}" for i in range(n_targets)])
A_df = pd.DataFrame(A.toarray(), columns=[f"Y{i}" for i in range(n_targets)], index=[f"X{i}" for i in range(n_features)])
# データ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
# XとYを結合
combined_df = pd.concat([X_df, Y_df], axis=1)
# 相関行列の計算
correlation_matrix = combined_df.corr()
# ヒートマップによる可視化
plt.figure(figsize=(12, 10))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('Correlation Matrix of X and Y')
plt.show()
A_df
これを実行すると、横結合行列[$X$,$Y$]の相関行列が可視化されます。
いま、$X$ は10次元, $Y$ は4次元としています。
説明変数同士には弱い相関しかないことがわかります。
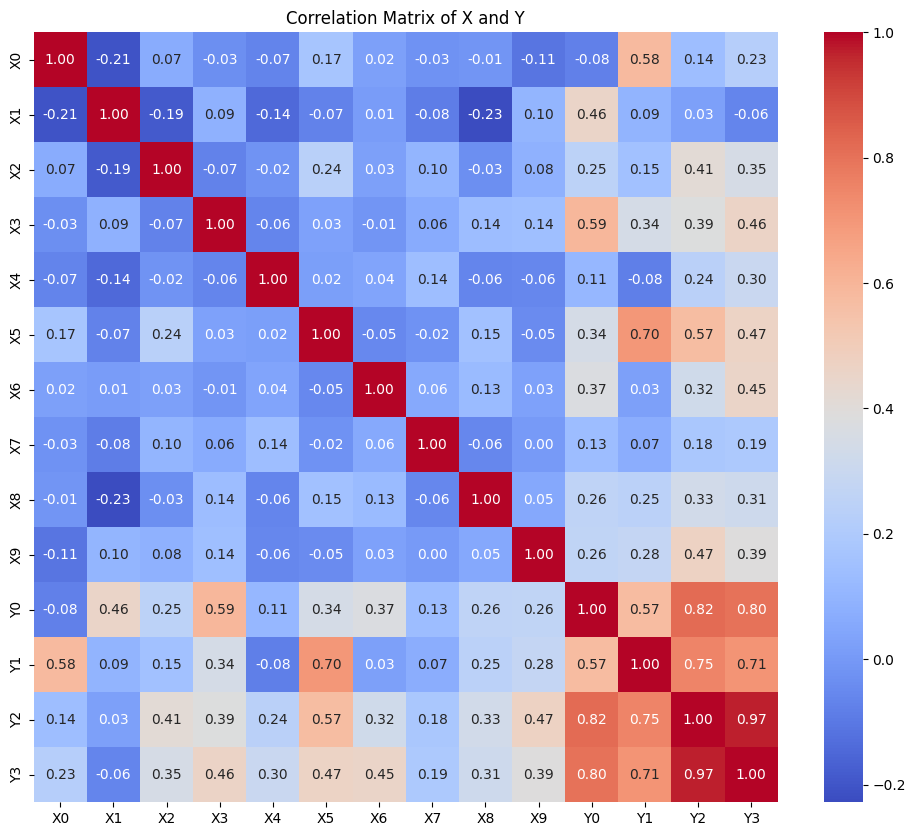
次にデータセット_ケース1を用いて線形回帰を実行します。
# Linear Regression モデルのインスタンス作成
lr_model = LinearRegression()
lr_model.fit(X_train, Y_train)
lr_pred = lr_model.predict(X_test)
lr_mse = mean_squared_error(Y_test, lr_pred)
print()
# 結果の比較
print(f"Mean Squared Error: {lr_mse}")
print()
# 正解の回帰係数 (A_df) と予測された回帰係数のプロット
plt.figure(figsize=(15, 5))
for i in range(n_targets): # 各ターゲット変数ごとにプロット
plt.subplot(1, n_targets, i + 1)
plt.plot(A_df.iloc[:, i], label="True Coefficients (A_df)", marker='o', linestyle='-')
plt.plot(lr_model.coef_[i], label="LinearRegression Coefficients", marker='^', linestyle='--')
plt.xlabel("Coefficient Index")
plt.ylabel("Coefficient Value")
plt.title(f"Y {i}")
plt.legend()
plt.tight_layout()
plt.show()
mse_list = []
for i in range(n_targets):
mse = mean_squared_error(A_df.iloc[:,i], lr_model.coef_[i])
mse_list.append(mse)
print(f"Y{i}: MSE between A_df and LinearRegression coefficients = {mse:.3f}")
print(f"\nAverage MSE: {np.mean(mse_list):.3f}")
これを実行すると目的変数ごとに回帰係数が算出されます。
A_dfが正解の回帰係数で、それとLinearRegressionの回帰係数を比較しています。
ここでは説明変数に相関がなく、回帰係数は高精度に求まっています。
(最後のMSEは正解と予測の差を計算しており、ここでは0でした)

説明変数に相関がある場合の回帰
次はデータセット_ケース2を使って検証します。
# データセットの作成
n_samples = 100
n_features = 10
n_targets = 4
X, y = make_regression(n_samples=100, n_features=10, n_targets=4, random_state=42)
X[:,1] = X[:,0]
X[:,3] = X[:,4]
X[:,7] = X[:,6]
# スパース行列Aの作成
# densitiyは0.2 or 1.0
A = random(n_features, n_targets, density=1.0, format="csr", random_state=42)
# Yの計算
Y = X @ A.toarray()
# データフレームへの変換
X_df = pd.DataFrame(X, columns=[f"X{i}" for i in range(n_features)])
Y_df = pd.DataFrame(Y, columns=[f"Y{i}" for i in range(n_targets)])
A_df = pd.DataFrame(A.toarray(), columns=[f"Y{i}" for i in range(n_targets)], index=[f"X{i}" for i in range(n_features)])
# データ分割
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=42)
# XとYを結合
combined_df = pd.concat([X_df, Y_df], axis=1)
# 相関行列の計算
correlation_matrix = combined_df.corr()
# ヒートマップによる可視化
plt.figure(figsize=(12, 10))
sns.heatmap(correlation_matrix, annot=True, cmap='coolwarm', fmt=".2f")
plt.title('Correlation Matrix of X and Y')
plt.show()
A_df
推定精度はどうなるでしょうか?
multico_test.pyを実行すると次の結果が得られます。

ここでは強相関のある次元($X_0$と$X_1$、$X_3$と$X_4$、$X_6$と$X_7$)で、
正解と予測に差があります。
よって、説明変数に強相関がある場合には回帰が低精度化することを
検証できました。
残課題
①高精度を保てる相関係数(またはVIF)の定量化
②シミュレーションで相関係数をコントロールする方法の調査(①の実施のため)
③目的変数の多重共線性についての検証
あたりが考えられます。
③は通常の回帰では考慮できないので、マルチタスク回帰が必要と思います。
ということで検証は以上です。
初投稿の感想ですが、書くの大変だなと思いました(小学生並みの感想)。
