EXCELで累乗近似曲線を引いたことで話が始まる
ある減衰していく時系列のデータがあって、普通にEXCELで近似曲線を引いてみたら累乗近似がいい感じだったので、業務の都合上EXCELではなくPythonで再現しようと思った。
やってみた結果、なぜか微妙に合わない…。なぜだろうと不思議に思ったところ以下の情報にたどり着いた。
Pythonによる累乗近似
ほとんどこのサイトを見れば解決するけども、自分の備忘録のために記事にする。
scipyのcurve_fitによる累乗近似とEXCELの累乗近似の違い
累乗の式を以下のように定義。
$y = bx^{a}$
scipyのcurve_fitは上記の式でデータと最も近似する$a$と$b$を返す非線形回帰を行っている。
ではEXCELではどうなのか。
上記の式は以下のような変換ができる。
$y = bx^{a}$
$\Rightarrow \ln y = \ln (bx^{a}) ・・・(対数をとる)$
$\Rightarrow \ln y = a\ln x + \ln b ・・・(右辺を分解)$
$\Rightarrow Y = aX + B ・・・(対数部分を新たな変数としてまとめる)$
このように累乗式の対数をとると$Y=aX+B$の線形回帰を行うことできる。
つまりEXCELの累乗近似は対数変換して線形回帰した結果を出力しているということらしい。
Pythonで実践してみる
ではPythonで実際どうなるのかやってみる。
データは内閣府のページにある「平成23年版 子ども・若者白書」の乳児死亡数・死亡率の推移のデータを使用する。
「平成23年版 子ども・若者白書」乳児死亡数・死亡率の推移
まずデータの読み込み
import numpy as np
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt
import pandas as pd
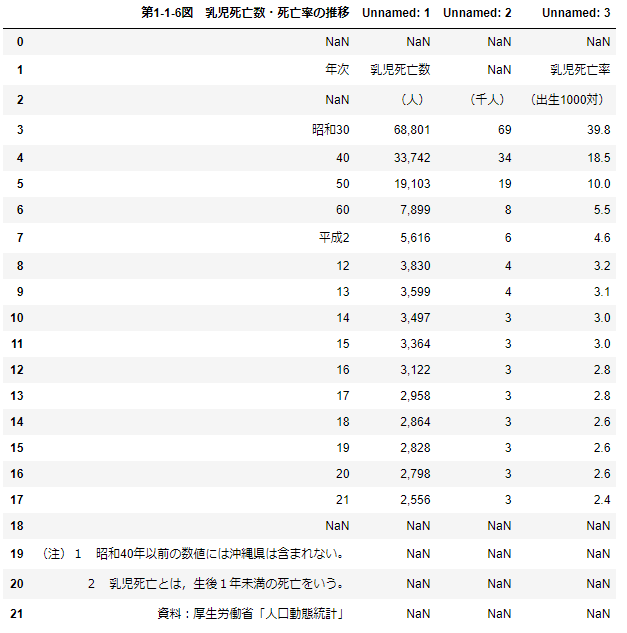
df=pd.read_csv('乳児死亡率.csv',encoding='cp932') # 文字化け防止でencoding='cp932'
display(df)
変な構成になっているので成形
df=df.iloc[3:18,:].rename(columns={'第1-1-6図 乳児死亡数・死亡率の推移':'年次'\
,'Unnamed: 1':'乳児死亡数(人)'\
,'Unnamed: 2':'乳児死亡数(千人)'\
,'Unnamed: 3':'乳児死亡率'})
# 後々の処理のために連番カラム作成
rank=range(1,len(df)+1)
df['rank']=rank
# すべてのカラムがobject型なので乳児死亡率をfloat型に
df['乳児死亡率']=df['乳児死亡率'].astype(float)
df['乳児死亡数(人)']=df['乳児死亡数(人)'].str.replace(',','').astype(np.int)
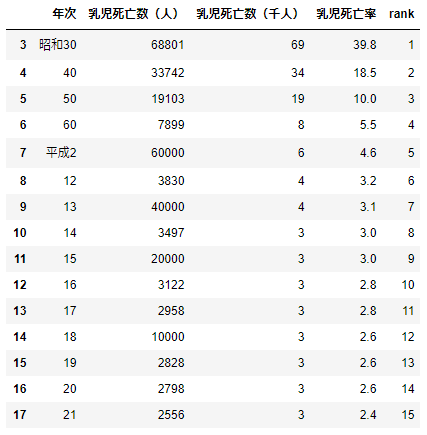
display(df)
乳児死亡率をplot
x=df['年次']
y=df['乳児死亡率']
ax=plt.subplot(1,1,1)
ax.plot(x,y)
ax.set_xlabel('年次')
ax.set_ylabel('乳児死亡率')
plt.show()
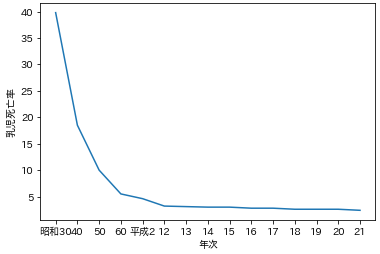
赤ん坊の死亡率は60年前から比べるとかなり下がってるんだなぁ。医療の進歩すごい。
ではいよいよ近似のパラメーターを求める段階へ。
scipyのcurve_fitで非線形回帰
def exp_func(x, a, b):
return b*(x**a)
def exp_fit(val1_quan, val2_quan):
# maxfev:関数の呼び出しの最大数, check_finite:Trueの場合NaNが含まれている場合はValueError発生
l_popt, l_pcov = curve_fit(exp_func, val1_quan, val2_quan, maxfev=10000, check_finite=False)
return exp_func(val1_quan, *l_popt),l_popt
exp_funcのパラメータ$a$と$b$をexp_fitを使って求める。
x=df['年次']
x2=df['rank']
y=df['乳児死亡率']
y_fit,l_popt=exp_fit(x2,y)
ax=plt.subplot(1,1,1)
ax.plot(x,y,label='obs')
ax.plot(x,y_fit,label='model')
ax.set_xlabel('年次')
ax.set_ylabel('乳児死亡率')
plt.legend()
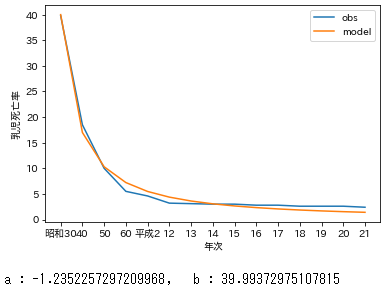
plt.show()
print('a : {}, b : {}'.format(l_popt[0],l_popt[1]))#求めたパラメータa,bを確認
良い感じ。
EXCELの累乗近似(対数変換して線形回帰)の再現
def exp_func_log(x, a, b):
return a*np.log(x) + np.log(b)
def exp_func_log_fit(val1_quan, val2_quan):
l_popt, l_pcov = curve_fit(exp_func_log, val1_quan, np.log(val2_quan), maxfev=10000, check_finite=False)
return exp_func_log(val1_quan, *l_popt),l_popt
def log_to_exp(x,a,b):
return np.exp(a*np.log(x) + np.log(b))
exp_func_logのパラメータ$a$と$b$をexp_func_log_fitを使って求める。
求めたパラメータ$a$と$b$を使って近似した$Y$は$\ln y$なのでlog_to_expで対数から変換して戻す。
x=df['年次']
x2=df['rank']
y=df['乳児死亡率']
y_fit,l_popt=exp_func_log_fit(x2,y)
y_fit=log_to_exp(x2,l_popt[0],l_popt[1])
ax=plt.subplot(1,1,1)
ax.plot(x,y,label='obs')
ax.plot(x,y_fit,label='model')
ax.set_xlabel('年次')
ax.set_ylabel('乳児死亡率')
plt.legend()
plt.show()
print('a : {}, b : {}'.format(l_popt[0],l_popt[1])) #求めたパラメータa,bを確認
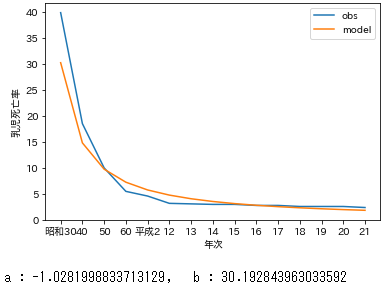
良い感じだけど、直接非線形回帰した方が当てはまりがよかった気がする。
まとめ
どっちが適切とかはよくわからない。
けど「EXCELではできたのにPythonで同じにならない!」っていう状況に陥ったらこれを思い出してみてもいいかもしれない。
追記(2020/02/28執筆直後)
データの数値が大きい かつ ぶれている時、非線形回帰での近似は数値の大きいぶれに引っ張られやすい。
汎化能力的な観点で言うと、対数変換して線形回帰の方が良いのかもしれない。
乳児死亡数(人)にダミーの数値を挿入する
df=pd.read_csv('乳児死亡率.csv',encoding='cp932')
df=df.iloc[3:18,:].rename(columns={'第1-1-6図 乳児死亡数・死亡率の推移':'年次'\
,'Unnamed: 1':'乳児死亡数(人)'\
,'Unnamed: 2':'乳児死亡数(千人)'\
,'Unnamed: 3':'乳児死亡率'})
# 後々の処理のために連番カラム作成
rank=range(1,len(df)+1)
df['rank']=rank
# すべてのカラムがobject型なので乳児死亡率をfloat型に
df['乳児死亡率']=df['乳児死亡率'].astype(float)
df['乳児死亡数(人)']=df['乳児死亡数(人)'].str.replace(',','').astype(np.int)
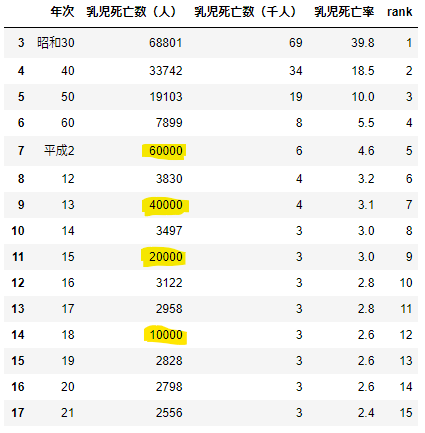
# ダミーデータを挿入する
df2=df.copy()
df2.loc[df2['年次']=='平成2', '乳児死亡数(人)']=60000
df2.loc[df2['年次']=='13', '乳児死亡数(人)']=40000
df2.loc[df2['年次']=='15', '乳児死亡数(人)']=20000
df2.loc[df2['年次']=='18', '乳児死亡数(人)']=10000
display(df2)
x=df2['年次']
y=df2['乳児死亡数(人)']
ax=plt.subplot(1,1,1)
ax.plot(x,y)
ax.set_xlabel('年次')
ax.set_ylabel('乳児死亡数(人)')
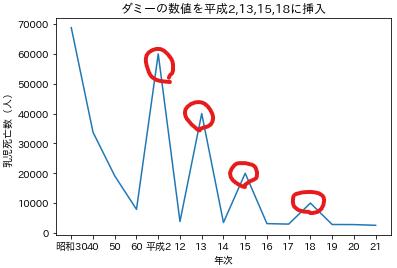
ax.set_title('ダミーの数値を平成2,13,15,18に挿入')
plt.show()
本編で使った関数を再度使用して近似曲線を引く
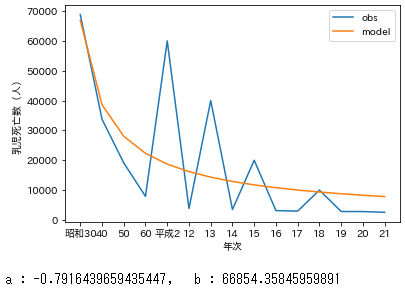
# 非線形回帰
x=df2['年次']
x2=df2['rank']
y=df2['乳児死亡数(人)']
y_fit,l_popt=exp_fit(x2,y)
ax=plt.subplot(1,1,1)
ax.plot(x,y,label='obs')
ax.plot(x,y_fit,label='model')
ax.set_xlabel('年次')
ax.set_ylabel('乳児死亡数(人)')
plt.legend()
plt.show()
print('a : {}, b : {}'.format(l_popt[0],l_popt[1]))
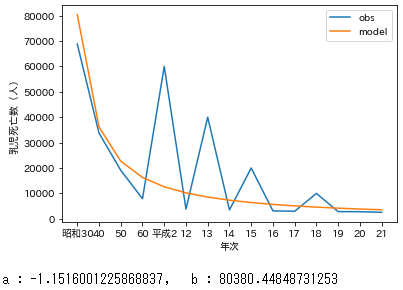
# 対数変換線形回帰
x=df2['年次']
x2=df2['rank']
y=df2['乳児死亡数(人)']
y_fit,l_popt=exp_func_log_fit(x2,y)
y_fit=log_to_exp(x2,l_popt[0],l_popt[1])
ax=plt.subplot(1,1,1)
ax.plot(x,y,label='obs')
ax.plot(x,y_fit,label='model')
ax.set_xlabel('年次')
ax.set_ylabel('乳児死亡数(人)')
plt.legend()
plt.show()
print('a : {}, b : {}'.format(l_popt[0],l_popt[1]))
明らかに非線形回帰で近似した方がダミーで入れた数値のぶれに引っ張られている。
区別して状況によって使い分けることが重要だと思われる。