pythonによる共分散構造分析 ～MMMを添えて～

はじめに

共分散構造分析をする時、どうすればいいだろうか。
Amos？いやいや有料だし、R？いやいやメインで普段使っていないし、python？いやいや共分散構造分析簡単にできないんじゃ…。

ﾄﾞｳｿﾞ( ´·ω·)つ [semopy]

ということでpythonで共分散構造分析が簡単に？できるsemopyを使用してみた。
実務で使うような想定でMMM(マーケティングミックスモデリング)の真似事をしながら試してみて、結果をlavaanやAmosの結果と比較した。
ちなみにMMMのことはほとんど知らないので調べながら実践。

結論を言うと、実務でも使えるツールだと思う。

参考文献

• 共分散構造分析[Amos編] － 豊田 秀樹(著)
• Pythonによるマーケティングミックスモデリング（MMM：Marketing Mix Modeling）超入門 その2
• MMM（マーケティングミックスモデル）をRobynでやってみた
• MetaのMMMパッケージ Robynを試してみる
• テレビCMの残存効果をAd Stock（アドストック）で計算してみる【R & Pythonコード付き】
• 早稲田大学パーソナリティ心理学研究室　心理データ解析　第10回(2)
• semopy
• semopy2
• マルチグーループSEM(多母集団同時分析) 配置不変モデル[Mplus]
• gitlab semopy

共分散構造分析

共分散構造分析は観測変数の背後にある、さまざまな要因の関係を分析する手法。要因とは直接は観測できない構成概念(ブランド価値、達成感…etc)も含まれる。
例えば因子分析における因子だったり、主成分分析における主成分だったりが構成概念と同じ意味を持つ。
共分散構造分析は観測変数や構成概念の複雑な関係をパス図というもので表現し、モデリングできる点が優れている。
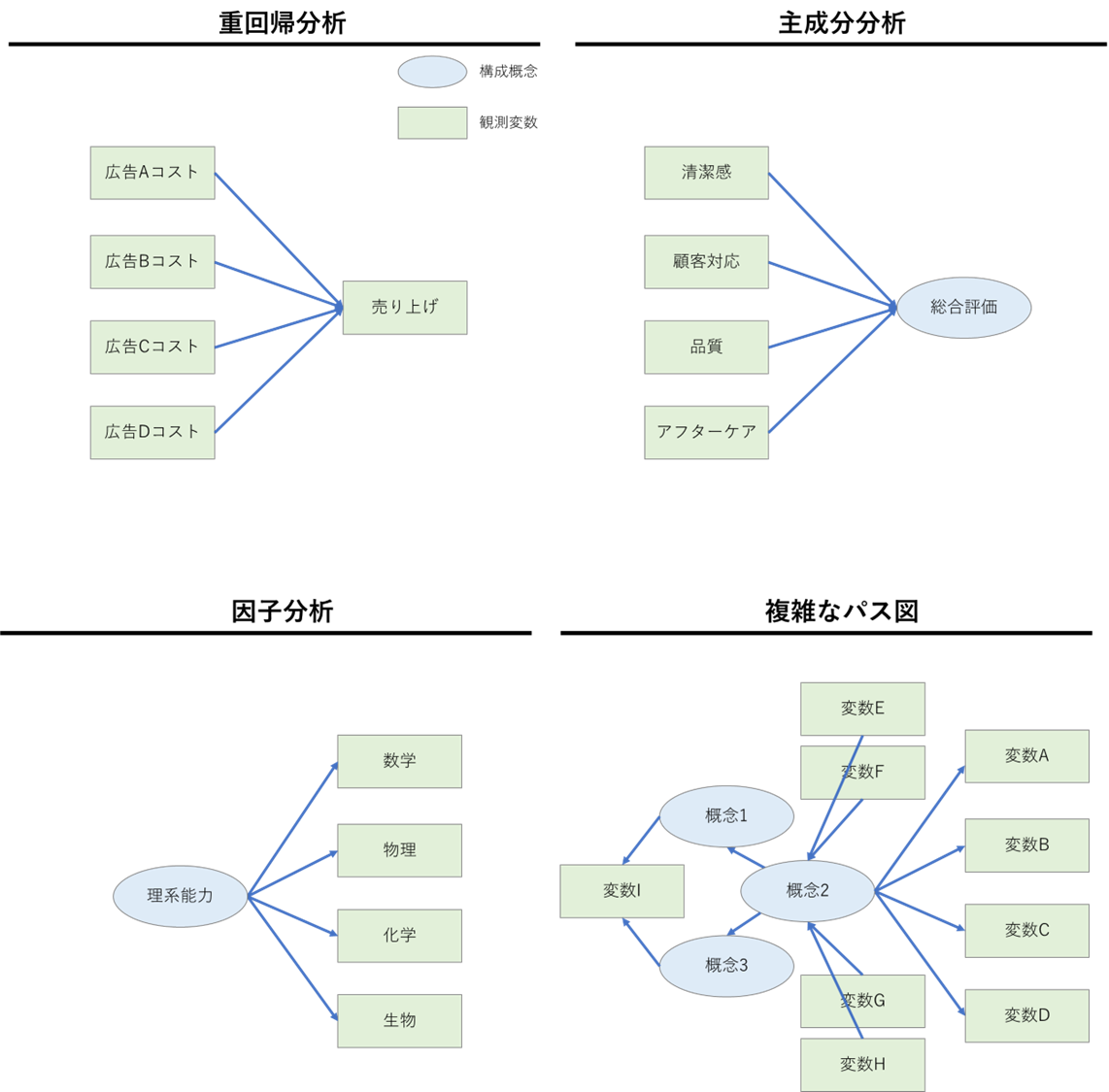
パス図とは以下の図のように観測変数、構成概念、それらの関係を四角、丸、矢印で表現したもので、パス図を使うことで、重回帰分析や因子分析、主成分分析をはじめ、複雑な分析モデルを表現できる。
パス図を使ってある程度自由にモデリングできるので、分析者の仮説とその分析結果を表現してくれる便利な道具である。
（参考：共分散構造分析[Amos編] － 豊田 秀樹(著)）

semopy

昔からRではlavaanというパッケージで共分散構造分析をお手軽？に実施できたし、またIBMのSPSS Amosという共分散構造分析専門のソフトを使えばGUI操作でお手軽にモデリングができた。
しかしpythonには共分散構造分析をお手軽に実施するためのツールは無い……と思っていた。
2019年に論文：semopyが書かれているsemopyというライブラリがありましたわ。（^ω^）
2021年にも論文：semopy2が書かれている。
2019年の論文のAbstractを翻訳（with DeepL）すると以下のように書いてある。

構造方程式モデリング（SEM）は、観測変数と潜在変数の間の複雑な関係を推定するための多変量統計手法である。多数のSEMパッケージが存在するが、それぞれに限界がある。このような欠点を持たない最も有名なパッケージはlavaanですが、これはR言語で書かれており、現在の主流から外れているため、開発パイプライン（例えばバイオインフォマティクス）に取り入れることが難しくなっています。そこで我々は、これらの条件を満たすPythonパッケージsemopyを開発した。本論文では、パッケージの詳細な使用例と内部動作の解説を行います。また、SEMパッケージの検証のため、独自のSEMモデル生成器を開発し、semopyが実行時間および精度でlavaanを大きく上回ることを実証した。

こうやって作っていただけるのは本当にありがたいこと(感謝)。だけども、他のツールの結果と矛盾するようなことはないのか？などいくつかテストはしておきたいと思ったので、今回Amosと比較してみようと思った。
一部lavaanと比較もしたが、自分がAmosを使える環境にいてせっかくなのでメインの部分はAmosと比較した。

簡単な比較(vs lavaan)

まずsemopyにもlavaanにも入っている、PoliticalDemocracyのデータでsemopyとlavaanを比較する。

lavaan

#### lavaan ####
library(lavaan)
library(semPlot)
# データの定義
data <- PoliticalDemocracy
# パス図の定義
model <- '
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
'
# モデル作成
fit <- sem(model, data = data)

# 結果テキスト表示
#summary(fit, standardized = TRUE)
# 係数の結果 csv output
#pathcoeff <- parameterEstimates(fit, standardized=FALSE) %>% filter(op == "=~")
#pathcoeff <- as.data.frame(pathcoeff)
#write.csv(pathcoeff, "lavaan_result_nonstd.csv")
#pathcoeff <- parameterEstimates(fit, standardized=TRUE) %>% filter(op == "=~")
#pathcoeff <- as.data.frame(pathcoeff)
#write.csv(pathcoeff, "lavaan_result_std.csv")

# 適合度表示
#fitMeasures(fit, fit.measures="all")

# パス図と結果表示
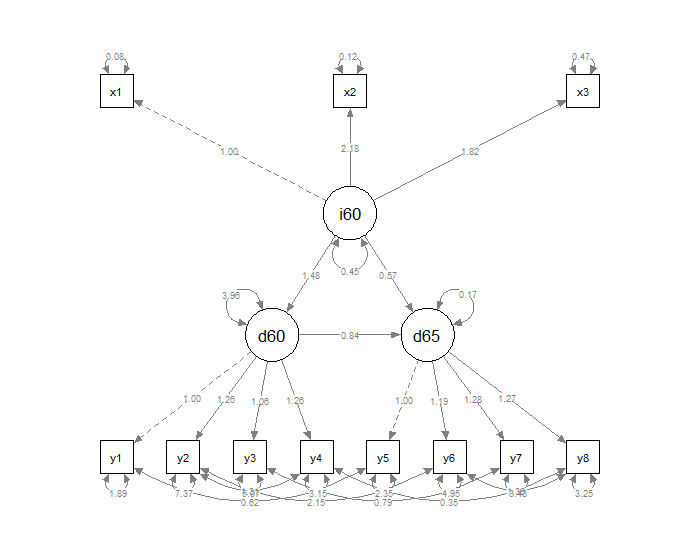
semPaths(object=fit, whatLabels="est") # 非標準化係数
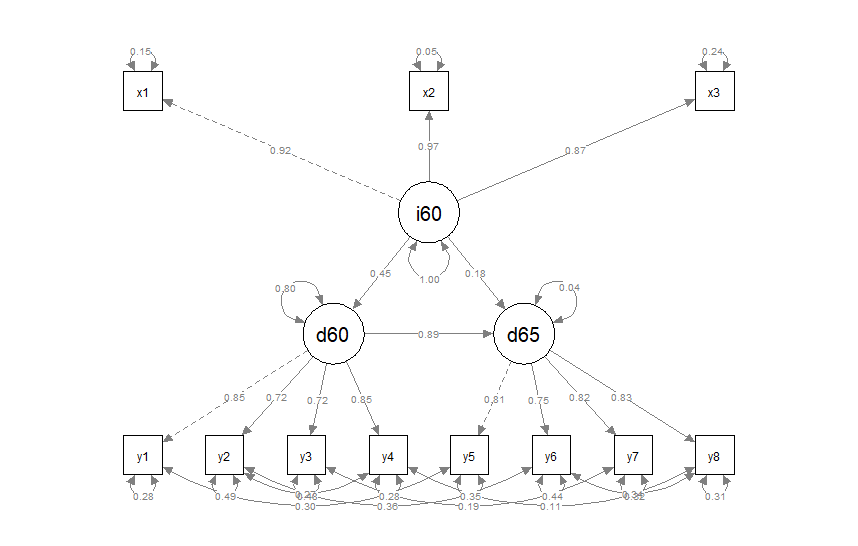
semPaths(object=fit, whatLabels="stand") # 標準化係数

非標準化係数

標準化係数

semopyもlavaanのように文字列でパス図を定義する。そしてsemopy.Modelでモデルをインスタンス化して、fitでデータをもとにモデリングする。

semopy

#### semopy ####
import numpy as np
import scipy
import matplotlib as mpl
from matplotlib import pyplot as plt
import matplotlib.font_manager as fm
import seaborn as sns
import pandas as pd
import sklearn
import semopy
jpn_fonts=list(np.sort([ttf for ttf in fm.findSystemFonts() if 'msgothic' in ttf]))
jpn_font=jpn_fonts[0]
prop = fm.FontProperties(fname=jpn_font)
sns.set()
print(semopy.__version__)
# > 2.3.9

# データ読み込み
data = semopy.examples.political_democracy.get_data()

# パス図定義
desc = semopy.examples.political_democracy.get_model()
print(desc)
'''
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
'''

# モデル作成
model = semopy.Model(desc)
model.fit(data)

# 結果テキスト表示
#display(model.inspect(std_est=True))
# 適合度表示
#display(semopy.calc_stats(model))

# 非標準化係数のパス図可視化
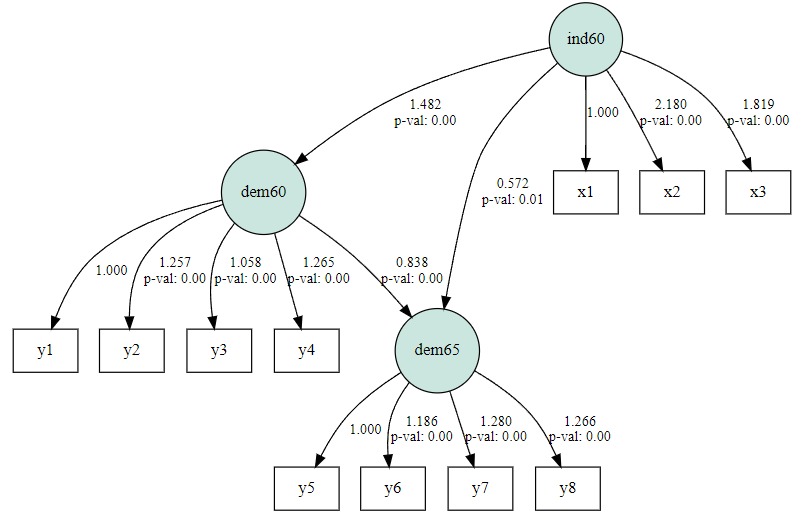
g = semopy.semplot(model, "tmp.png", plot_covs=False)
display(g)

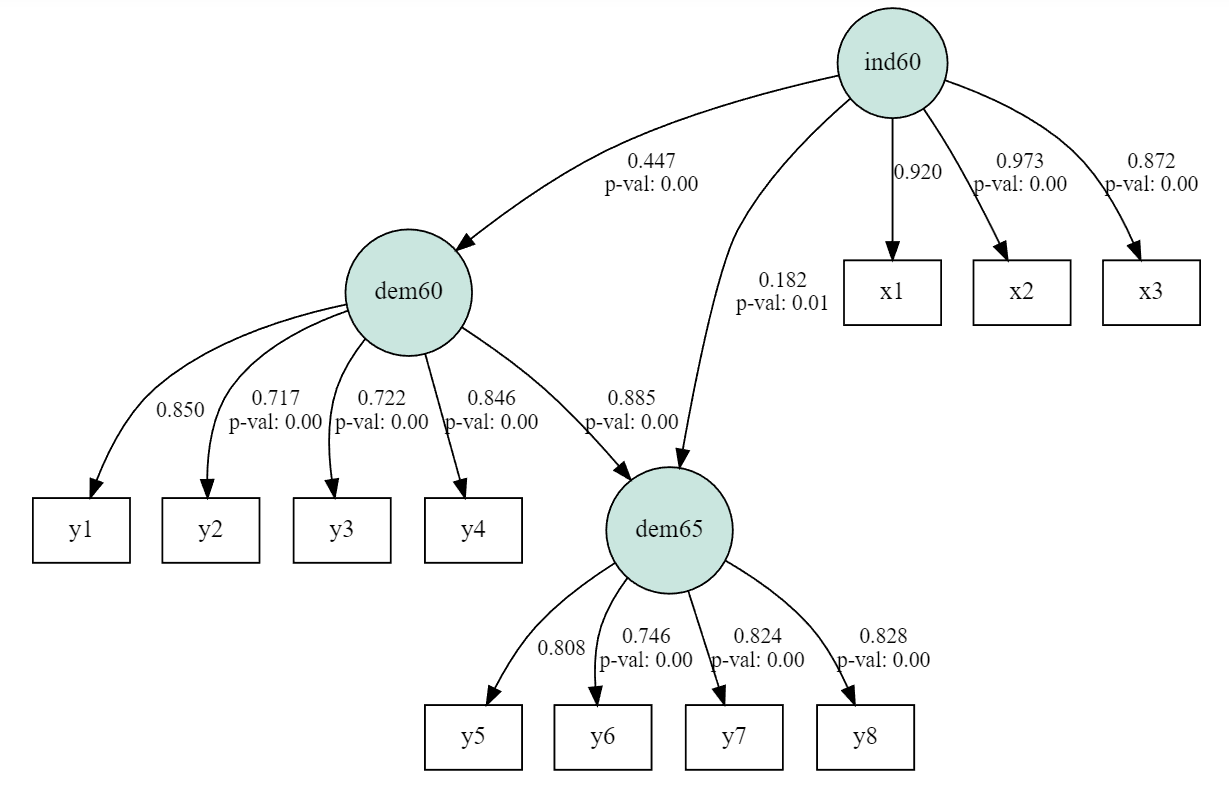
# 標準化係数のパス図可視化
g = semopy.semplot(model, "tmp.png", plot_covs=False, std_ests=True)
display(g)

非標準化係数

標準化係数

比較結果

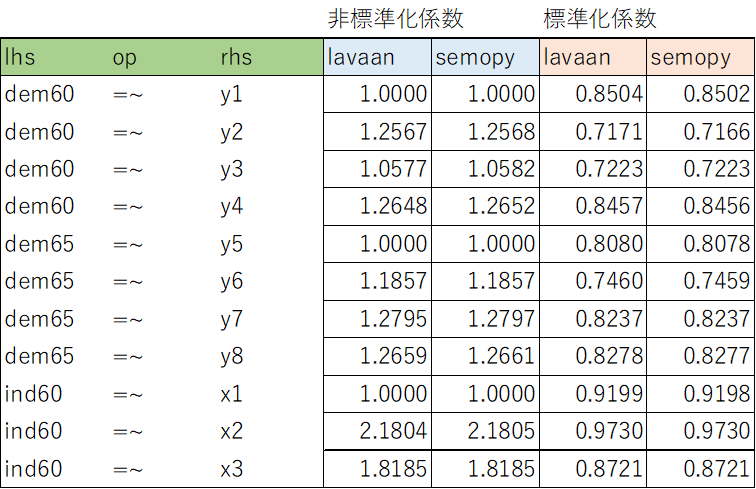
lavaanとsemopyの結果をテキスト出力してまとめたものが以下。
小数点2桁くらいまでは同じ結果になっていた。ふむふむ。

MMMの真似事で比較(vs Amos)

データ

RのパッケージRobynのdemoコードにあるサンプルデータを使ってAmosとsemopyを比較していく。
サンプルデータは、週ごとの広告のインプレッション、クリックなどのデータと売り上げデータが入っている。（ぶっちゃけ詳細はあまり知らない。休日に関するデータは今回は無視。）
休日効果とか広告効果の飽和とか考えないといけないと思うんだけど…真似事なので無視！
とりあえず以下の変数を使ってモデリングしてみる。
参照：MMM（マーケティングミックスモデル）をRobynでやってみた

revenue： 売り上げ
tv_S： TV広告への投資量
ooh_S： OOH広告への投資量
print_S： 印刷媒体広告への投資量
search_S： 検索エンジン広告への投資量
facebook_S： Facebook広告への投資量
search_clicks_P： 検索エンジンでの広告のクリック数
facebook_I： Facebook広告のインプレッション数
competitor_sales_B： ある同分野競合他社の売り上げ
newsletter： ニュースレター配信、プッシュ通知など広告以外のマーケティング活動

サンプルデータ：dt_prophet_holidays.RData
.RDataとなっているので、Ｒで読み込んで、csvとして吐き出しておく。

# R
data <- load("dt_simulated_weekly.RData")
write.csv(data, file = "dt_simulated_weekly.csv", row.names = TRUE)

前処理

まずはもろもろ前処理をしていく。
データ読み込み。

import numpy as np
import scipy
import matplotlib as mpl
from matplotlib import pyplot as plt
import matplotlib.font_manager as fm
import seaborn as sns
import pandas as pd
import sklearn
import semopy
jpn_fonts=list(np.sort([ttf for ttf in fm.findSystemFonts() if 'msgothic' in ttf]))
jpn_font=jpn_fonts[0]
prop = fm.FontProperties(fname=jpn_font)
sns.set()
print(semopy.__version__)
# > 2.3.9

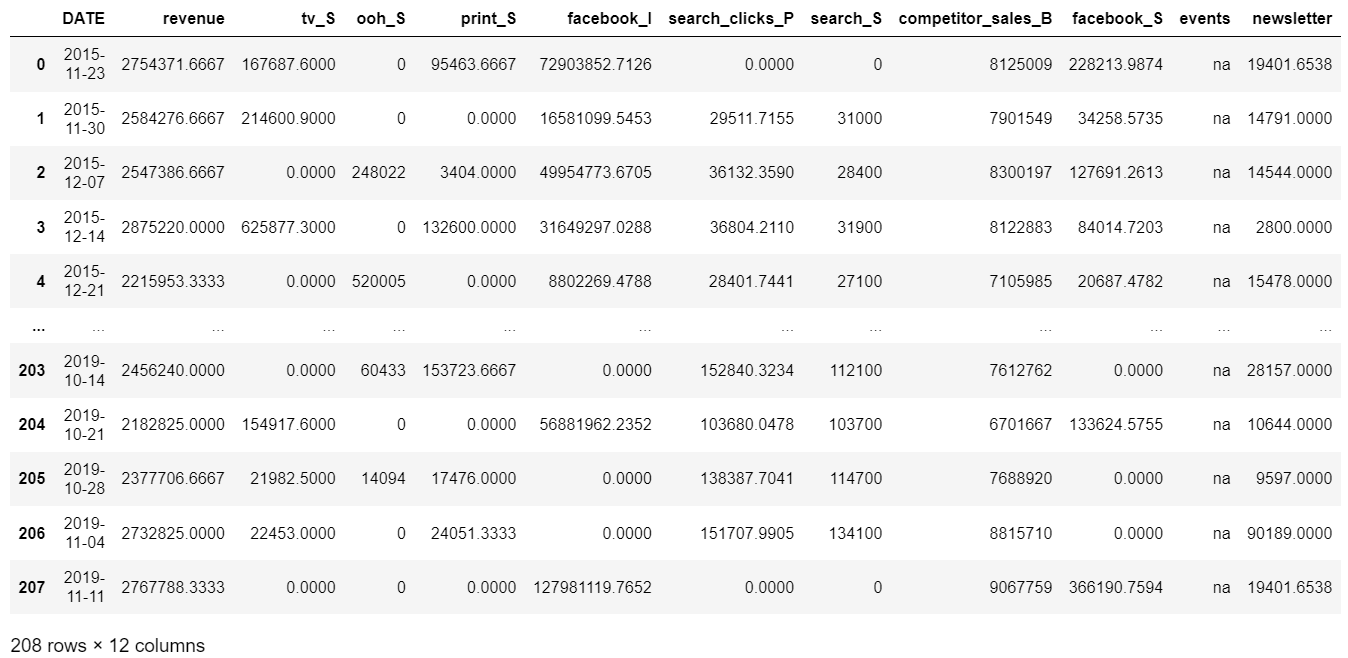
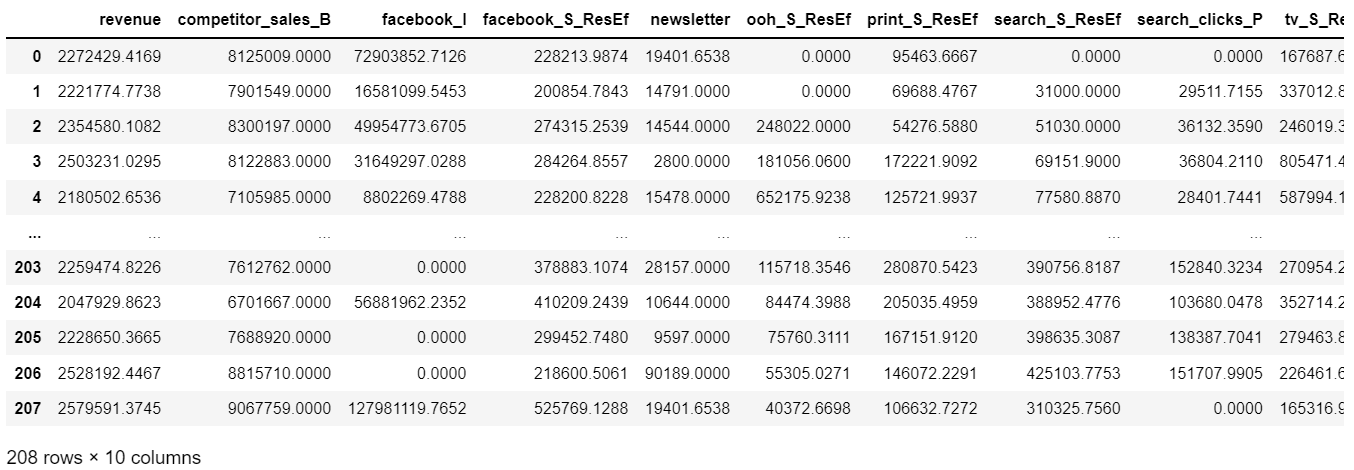
mmmDf = pd.read_csv('dt_simulated_weekly.csv').iloc[:,1:]
mmmDf['DATE'] = pd.to_datetime(mmmDf['DATE'])
display(mmmDf)

アドストック

MMMにおいてアドストックを考慮するために「テレビCMの残存効果をAd Stock（アドストック）で計算してみる【R & Pythonコード付き】」の記事を参考にさせていただいた。

広告の残存効果をモデル化したアドストックという指標を導入する。

広告を打った初週だけでなく、 翌週、翌々週以降も効果が残存しているという設定でモデルを定式化する。

時点tでの残存効果（アドストック）Atを以下のように定義する。
$A_t=T_t+λA_{t−1}$
ただし、
$A_t$：時点tでのAdStock
$T_t$：時点tでの広告指標（たとえば視聴率）
$λ$：忘却率（減衰率・残存率）
※どれくらいの割合で減衰していくかを表す定数(0から1の間の数値を取る)

残存効果を計算する関数。

# 残存効果を計算する関数
def residual_effect(df, col_list, eta = 0.8, date='DATE'):
    '''
    At=Tt+λAt−1
    '''
    data = df.copy()
    for col in col_list:
        data[col+'_ResEf']=data[col]
        dataRE=data[col+'_ResEf'].copy()
        Yb = 0
        tmp = []
        for val in dataRE:
            tmp.append(val+eta*Yb)
            Yb = val+eta*Yb
        data[col+'_ResEf']=tmp
    return data

忘却率をどうやって決めるか

忘却率が0.01のとき、0.02のとき、・・・、0.98のとき、0.99のとき、と忘却率を100通り試して、 アドストックと広告効果の相関が最も高くなるようなパラメータを選びとればよい。

col_list = ["tv_S", "ooh_S", "print_S", "facebook_S", "search_S"] # 広告系変数

cr = 0 # 相関係数
date='DATE'
# 売り上げ変数
obj_col = 'revenue'
# 忘却率を0.1から1まで21通り設定して、
# 残存効果を考慮した各広告系変数と売り上げ(revenue)の相関係数の平均が高くなる忘却率を選択
for eta in np.linspace(0.1,1,21):
    # 残存効果計算
    mmmDfResEf = residual_effect(mmmDf, col_list, eta = eta, date='DATE')#[[obj_col]+col_list]
    # 残存効果計算後の変数名抽出
    exp_col = [c for c in mmmDfResEf.columns if '_ResEf' in c]
    # 売り上げ(revenue)と残存効果計算後の変数のdf
    mmmDfResEf = mmmDfResEf[[date, obj_col, 'newsletter']+exp_col]
    # 売り上げ(revenue)変数と残存効果計算後の変数の相関係数計算して平均を取る
    # 前のcrより高ければ忘却率とcrを更新
    if mmmDfResEf.corr().iloc[2:,0].mean()>cr:
        etaans = eta
        cr = mmmDfResEf.corr().iloc[2:,0].mean()
print(etaans, cr)
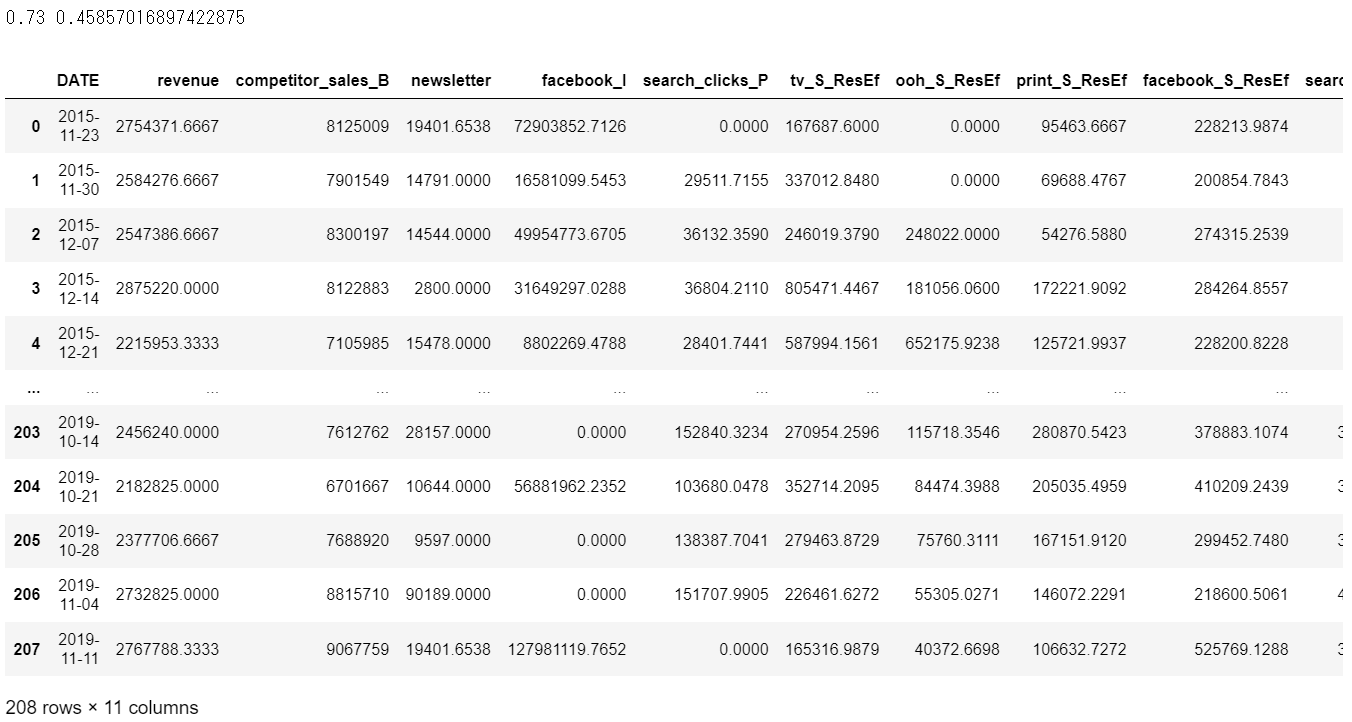
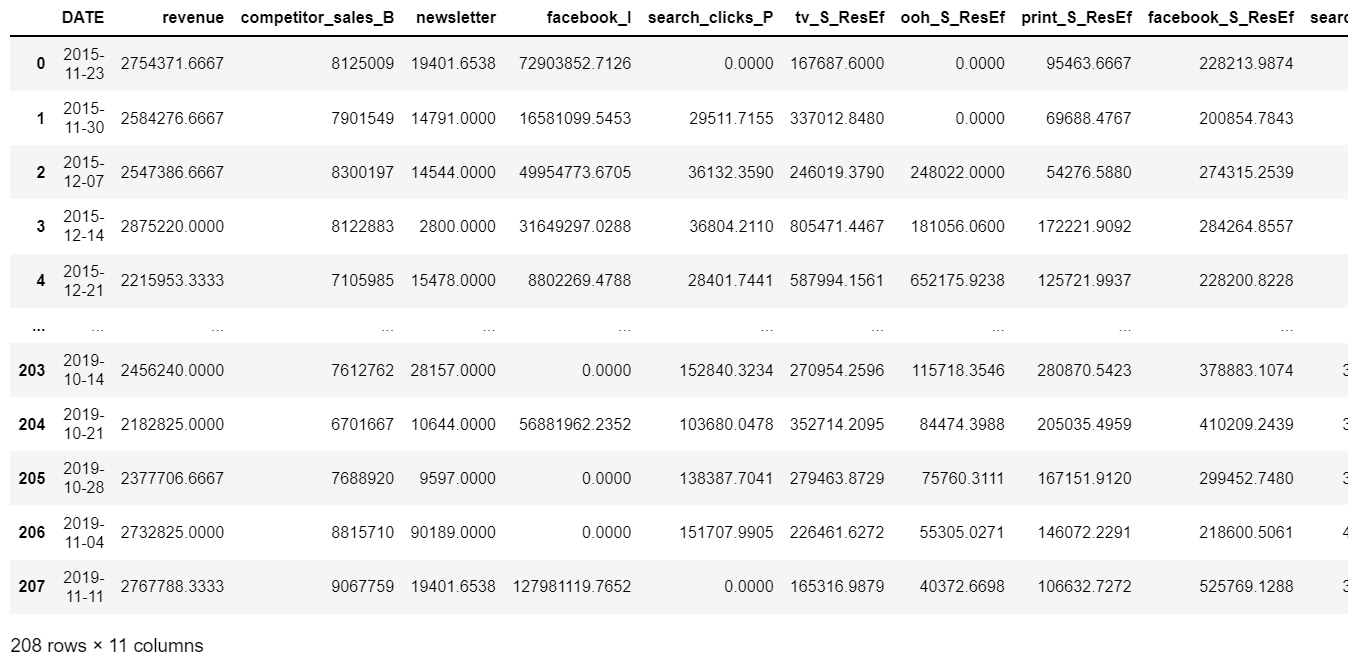
# 最も相関が高かった忘却率で残存効果再計算
mmmDfResEf = residual_effect(mmmDf, col_list, eta = etaans, date='DATE')
exp_col = [c for c in mmmDfResEf.columns if '_ResEf' in c]
mmmDfResEf = mmmDfResEf[[date, obj_col, 'competitor_sales_B', 'newsletter', 'facebook_I', 'search_clicks_P']+exp_col]
display(mmmDfResEf)
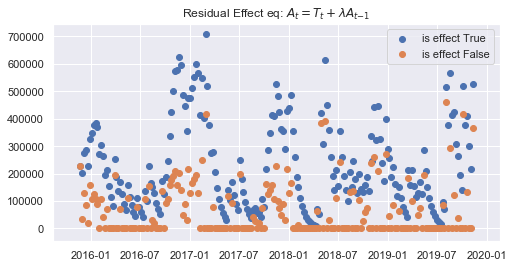
# 残存効果計算前と計算後の'facebook_I_ResEf'の結果プロット
fig = plt.figure(figsize=(8,4))
plt.scatter(mmmDfResEf[date], mmmDfResEf['facebook_S_ResEf'], label='is effect True')
plt.scatter(mmmDfResEf[date], mmmDf['facebook_S'], label='is effect False')
plt.title("Residual Effect eq: $A_{t}=T_{t}+λA_{t−1}$")
plt.legend()
plt.show()

'facebook_S'の計算結果

残存効果を計算し終わったので、モデルを作ると言いたいが、ここで疑問。
けっこう変数ごとにスケールが違うし、なんなら単位も違うものがあるけど、標準化しなくてもいいのか、という疑問。
標準化係数は出るけど、そもそもモデル作る時に標準化しなくていいのか？
そのままモデルを作った時の標準化係数と、標準化したデータで作ったモデルの非標準化係数が異なっていたのでどうするべきなのかわからなくなってしまった…。もっと理論部分も勉強しないとな…。
今回は、とりあえず標準化せずモデルを作ることにした。

# 標準化はしない
#mmmDfResEf_std = (mmmDfResEf.iloc[:,1:]-mmmDfResEf.iloc[:,1:].mean())/mmmDfResEf.iloc[:,1:].std()
mmmDfResEf_std = mmmDfResEf.iloc[:,1:].copy()
mmmDfResEf_std.insert(0, 'DATE', mmmDfResEf.DATE)
display(mmmDfResEf_std)

モデル作成

ではパス図を作る。（データをよく理解していないので適当）

• 競合の売り上げのcompetitor_sales_Bとオーガニックのnewsletterはrevenueに直接つながる。
• search_Sやfacebook_Sのオンライン広告系はsearch_clicks_Pやfacebook_Iをそれぞれ経由して構成概念につながり、構成概念からrevenueにつながる。
• tv_Sやprint_S、ooh_Sのオフライン広告系は構成概念につながり、構成概念からrevenueにつながる。

competitor_sales_Bで業界特有の季節性とかをモデルに含ませられればいいなと思っている。

desc = \
'''
# regressions
revenue ~ competitor_sales_B
revenue ~ newsletter
facebook_I ~ facebook_S_ResEf
search_clicks_P ~ search_S_ResEf
interest ~ search_clicks_P + facebook_I
awareness ~ tv_S_ResEf + print_S_ResEf + ooh_S_ResEf

# Measurement part
awareness =~ revenue
interest =~ revenue

# residual correlations
facebook_S_ResEf ~~ search_S_ResEf
facebook_S_ResEf ~~ ooh_S_ResEf
facebook_S_ResEf ~~ print_S_ResEf
facebook_S_ResEf ~~ tv_S_ResEf
facebook_S_ResEf ~~ newsletter
facebook_S_ResEf ~~ competitor_sales_B
search_S_ResEf ~~ ooh_S_ResEf
search_S_ResEf ~~ print_S_ResEf
search_S_ResEf ~~ tv_S_ResEf
search_S_ResEf ~~ newsletter
search_S_ResEf ~~ competitor_sales_B
ooh_S_ResEf ~~ print_S_ResEf
ooh_S_ResEf ~~ tv_S_ResEf
ooh_S_ResEf ~~ newsletter
ooh_S_ResEf ~~ competitor_sales_B
print_S_ResEf ~~ tv_S_ResEf
print_S_ResEf ~~ newsletter
print_S_ResEf ~~ competitor_sales_B
newsletter ~~ competitor_sales_B
'''
# モデル作成
model = semopy.Model(desc)
model.fit(mmmDfResEf_std.iloc[:,1:])
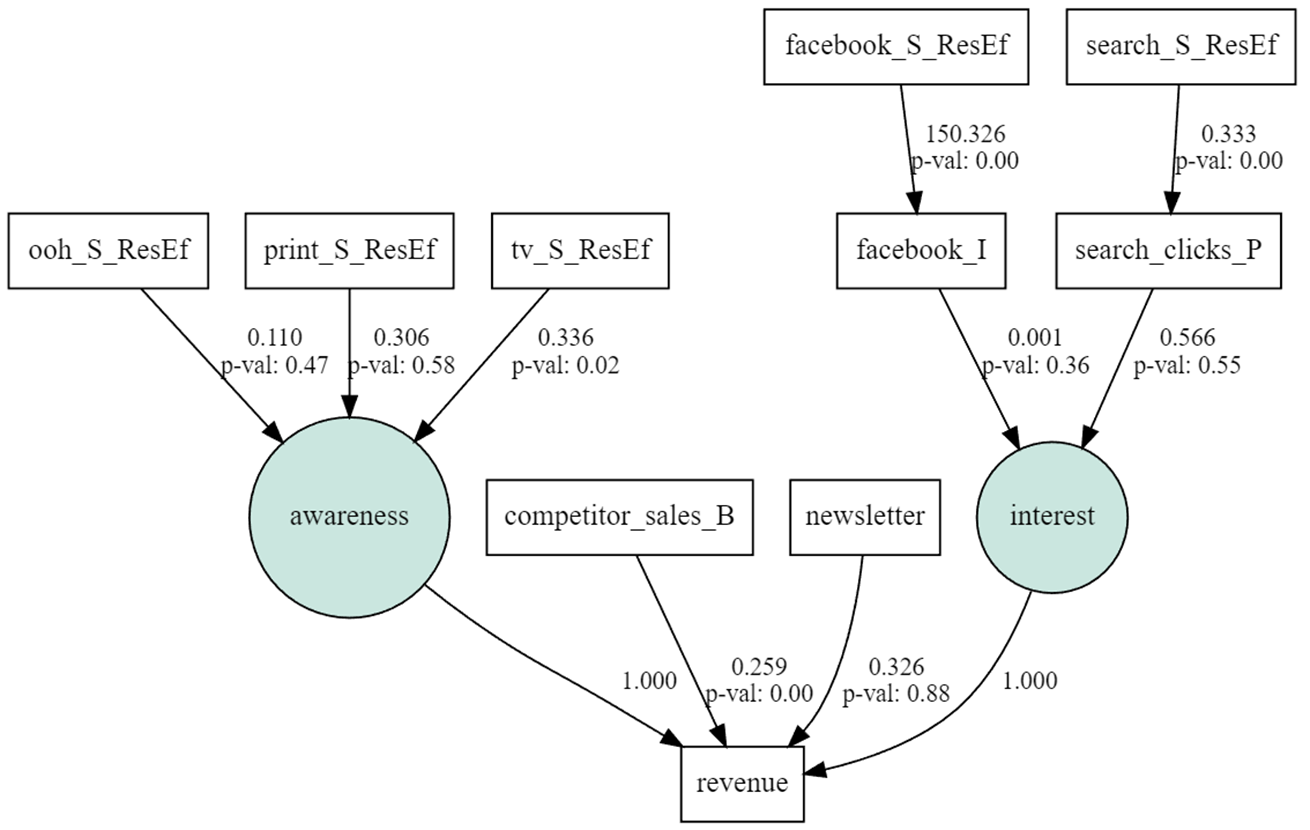
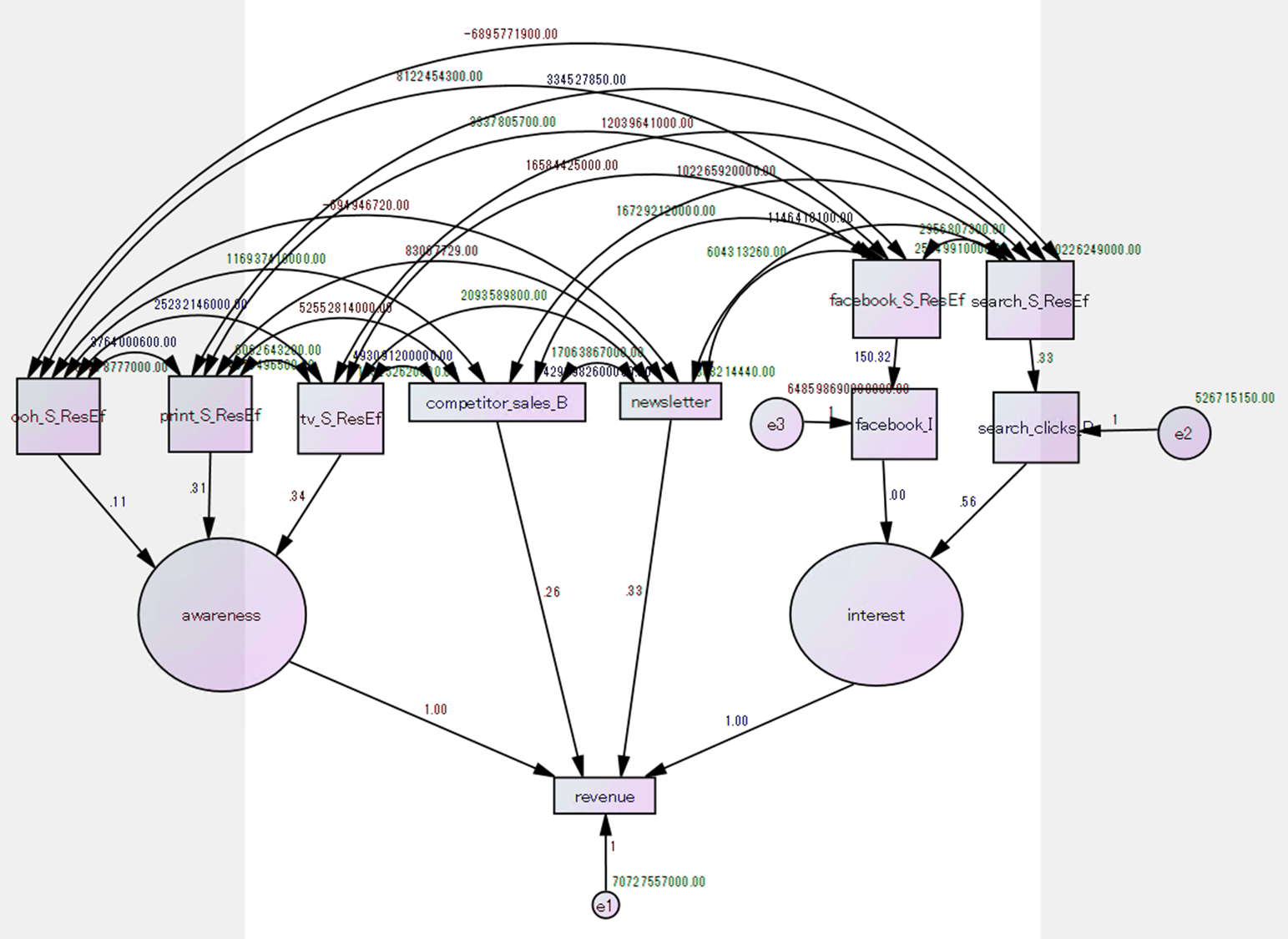
g = semopy.semplot(model, "tmp.png", plot_covs=False)
display(g)
# display(semopy.calc_stats(model).T) # 適合度見られる

非標準化係数（共分散は非表示）

同じデータを使ってAmosで共分散構造分析をポチポチと実施。
非標準化係数

比較結果

Amosとsemopyの結果をテキスト出力してまとめたものが以下。
だいたい小数点3桁くらいまでは同じ結果になっていた。

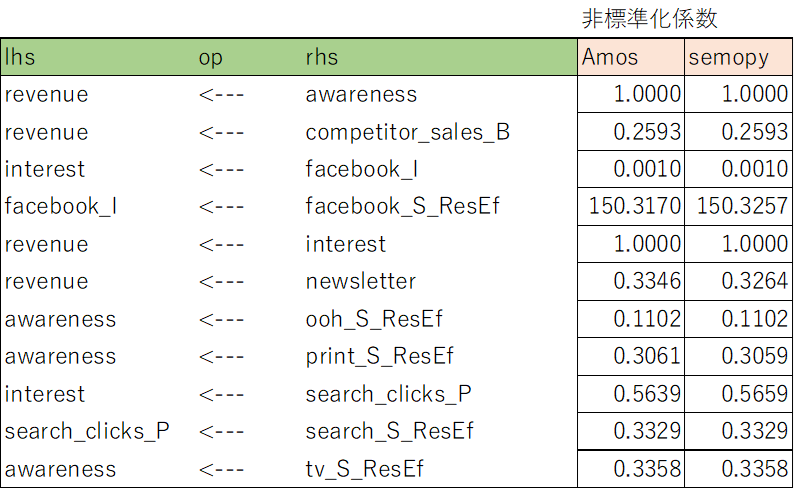
ということで出力結果は、lavaanとも、Amosともほとんど同じになることを確認できた。
semopy使えます！

モデルによる推定

ちなみにsklearnよろしく、model.predict()で変数の予測もできます。
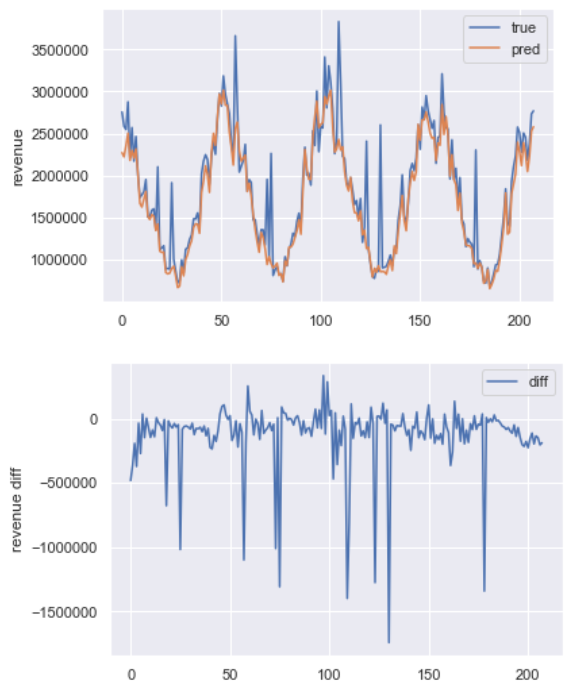
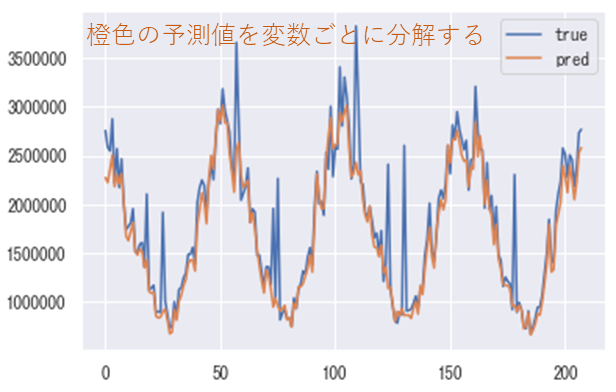
revenueの予測をやってみた結果は以下。

# 実測
true = mmmDfResEf['revenue']
# 予測
pred = model.predict(mmmDfResEf_std.iloc[:,2:])
display(pred) # 返される結果
# 標準化を戻す
pred = (pred['revenue'])#*mmmDfResEf.iloc[:,1].std())+mmmDfResEf.iloc[:,1].mean()

# 実測と予測プロット
plt.plot(true, label='true')
plt.plot(pred, label='pred')
plt.legend()
plt.ylabel('revenue')
#plt.ylim(0,)
plt.show()

# 予実差プロット
plt.plot(pred-true, label='diff')
plt.legend()
plt.ylabel('revenue diff')
#plt.ylim(-1900000,1900000)
plt.show()

総合効果の計算

と、semopyのテストはここまでで十分ということで、MMMの真似事を進めようと思う。
Amosで出力した後見ることができる総合効果を、semopyの結果からも計算して、各広告がどれくらいrevenueに効果があるかを計算する。
Amosの総合効果↓

変数がrevenueに直接つながっているとその係数を直接効果といい、他の変数や構成概念を経由してrevenueにつながっているとき経由したパスの係数のかけ算を間接効果といい、総合効果=直接効果+間接効果となる。
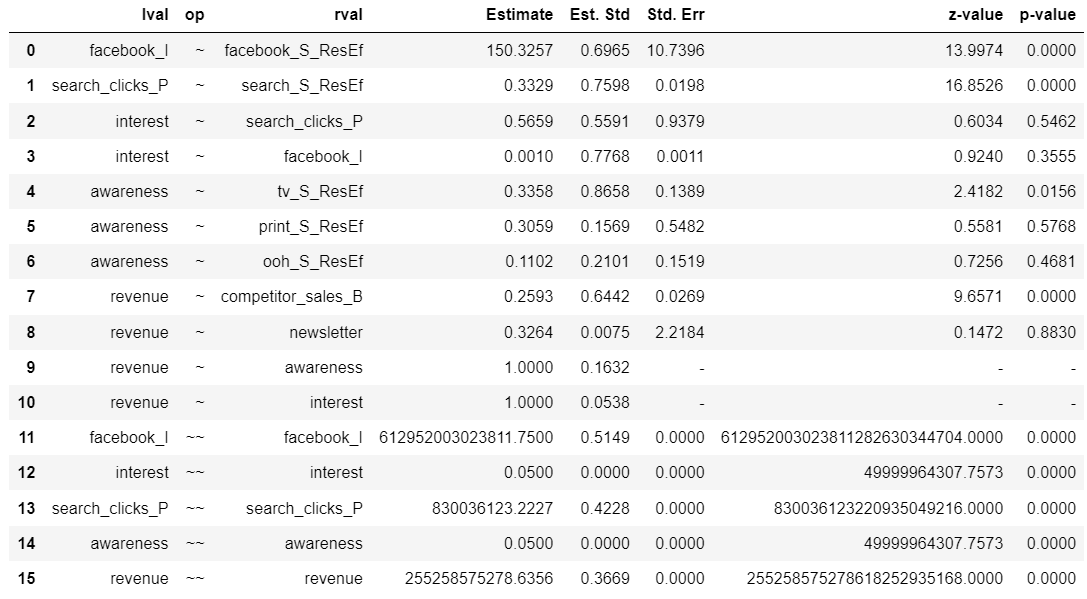
各係数はmodel.inspect()で出力でき、その出力から総合効果を計算する。

# 変数名定義
cols = ['competitor_sales_B','newsletter','tv_S_ResEf','print_S_ResEf','ooh_S_ResEf','search_S_ResEf','facebook_S_ResEf']
# 出力
ins = model.inspect(std_est=True)
display(ins)

起点ノード→中間ノード→・・・→終点ノードという形で係数をまとめるデータフレームを作る。(作るのに苦戦したので汎用性はなさそう)

def path_summary(ins_org, colname, objcol='revenue', epoch=10000):
    ins = ins_org[ins_org['op']!='~~'].copy()
    phase_list = []
    # 起点から終点までの経由ノード数をepoch数分回してdfを作る
    for step in range(epoch):
        # step=0の時、'rval'!='lval'のdf[['rval', 'lval', 'Estimate']]をリストに入れる
        if step==0:
            phase_list.append(ins[(ins['rval']==colname)&(ins['rval']!=ins['lval'])][['rval', 'lval', 'Estimate']])
            
        # step>0の時
        else:
            # phase_listの最後のdfの行数が1のとき、
            # かつそのdfの'lval'にobjcolがある時、ループ終了
            if len(phase_list[-1])==1 and objcol in phase_list[-1]['lval']:
                break
            # phase_listの最後のdfの行数が0のとき、削除してループ終了
            elif len(phase_list[-1])==0:
                phase_list.pop(-1)
                break
            # phase_listの最後のdfの'lval'と同じ変数が'rval'にあり、
            # 'rval'!='lval'である結果を抽出
            else:
                phase_list.append(ins[(ins['rval'].isin(phase_list[-1]['lval']))\
                                      &(ins['rval']!=ins['lval'])
                                     ][['rval', 'lval', 'Estimate']]
                                 )
    # phase_listが空の時例外
    if len(phase_list)==0:
        raise Exception
    # phase_listのdfそれぞれを処理して起点→中間→終点のパス図を表にまとめる
    for i in range(len(phase_list)):
        # phase_listの中身が1のとき、そのまま定義して終了
        if len(phase_list)==1:
            phase = phase_list[0].rename(columns={'Estimate':'Estimate'+str(i+1)})
            break
            
        # 0番目の処理はスキップ
        if i==0:
            continue
        # 1番目の処理=0番目のdfと1番目のdfを'lval'と'rval'マージしてphaseと定義
        elif i==1:
            phase = pd.merge(phase_list[i-1].rename(columns={'lval':'middle'+str(i),'Estimate':'Estimate'+str(i)})
                             , phase_list[i].rename(columns={'rval':'middle'+str(i),'Estimate':'Estimate'+str(i+1)})
                             , on=['middle'+str(i)]
                             , how='left')
            #display(phase)
        # 以降の処理=前回のphaseとi番目のdfを'lval'と'rval'マージしてphaseと定義
        else:
            phase = pd.merge(phase.rename(columns={'lval':'middle'+str(i),'Estimate':'Estimate'+str(i)})
                             , phase_list[i].rename(columns={'rval':'middle'+str(i),'Estimate':'Estimate'+str(i+1)})
                             , on=['middle'+str(i)]
                             , how='left')
            #display(phase)
    # カラムをrval→middle→lvalの順番に変更して係数をその右側に持ってくる
    colnode = [col for col in phase.columns if 'middle' in col]
    colesti = [col for col in phase.columns if 'Estimate' in col]
    phase = phase[['rval']+colnode+['lval']+colesti]
    return phase

それぞれの観測変数で処理を実施。

# 目的変数
objcol='revenue'
# 観測変数ごとに処理を実施してconcat
summaries = [path_summary(ins, col, objcol=objcol, epoch=10000) for col in cols]
summaries = pd.concat(summaries)
# ノード名のカラム名と、係数のカラム名をそれぞれ取得
colnode = [col for col in summaries.columns if 'middle' in col]
colesti = [col for col in summaries.columns if 'Estimate' in col]
# 起点ノード→中間ノード→・・・→終点ノードという形で係数をまとめるデータフレーム
summaries = summaries[['rval']+colnode+['lval']+colesti].reset_index(drop=True)
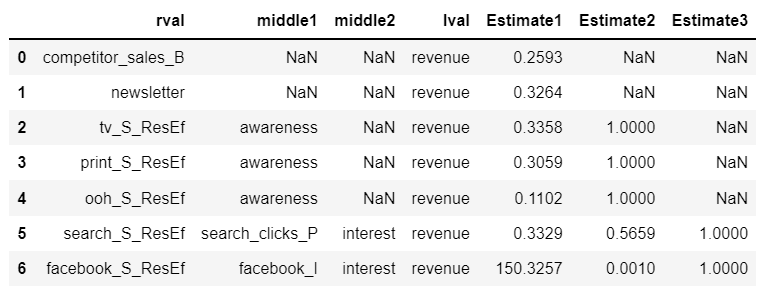
display(summaries)

上記のように、起点ノード→中間ノード→・・・→終点ノードという形のdfが完成。

• newsletterとcompetitor_sales_Bは直接revenueにつながっているので、middle1, middle2はNaNでlvalがrevenue、そしてEstimate1に係数が入っているだけ。
• tv_S_ResEf, ooh_S_ResEf, print_S_ResEfはawarenessを経由してrevenueにつながっているので、middle1はawareness、middle2はNaNでlvalがrevenue、そしてEstimate1にawareness方向への係数、Estimate2にawareness→revenueの係数が入っている。
• search_S_ResEf, facebook_S_ResEfは別の観測変数を1つ経由した後interestを経由してrevenueにつながっているので、middle1は観測変数、middle2はinterestでlvalがrevenue、そしてEstimate1に別の観測変数方向への係数、Estimate2にinterest方向への係数、Estimate3にinterest→revenueの係数が入っている。

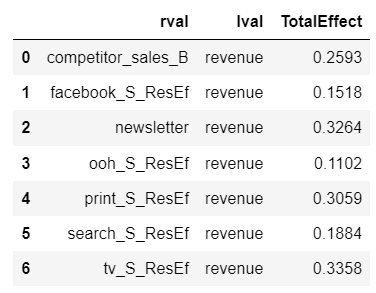
このdfから観測変数ごとのrevenueへの総合効果を計算。

# 結果を入れる箱
objcolDf_list = []
# 'rval'、middle、'lval'のカラムを取ってくる
for col in ['rval']+colnode+['lval']:
    # colの行にobjcolがある行を抽出
    objcolDf = summaries[summaries[col].isin([objcol])].copy()
    # objcolDfが存在していたら、
    # objcolまでの係数をかけ算(objcol直通なら直接効果、経由地があれば間接効果)
    if len(objcolDf)>0:
        # ['rval', col]とEstimateだけ抜き出し、colは'lval'に名前変更
        objcolDf = objcolDf[['rval', col]+colesti].drop_duplicates().rename(columns={col:'lval'})
        # objcolまでの係数をかけ算
        objcolDf['Effect'] = objcolDf.prod(axis=1, numeric_only=True).to_numpy()
        objcolDf_list.append(objcolDf[['rval', 'lval', 'Effect']])
# 観測変数ごとに直接効果、間接効果を計算できたので足し合わせて総合効果とする
objcolDf = pd.concat(objcolDf_list).reset_index(drop=True)
objcolDf = objcolDf.groupby(['rval', 'lval'])[['Effect']].sum().reset_index().rename(columns={'Effect':'TotalEffect'})
display(objcolDf)

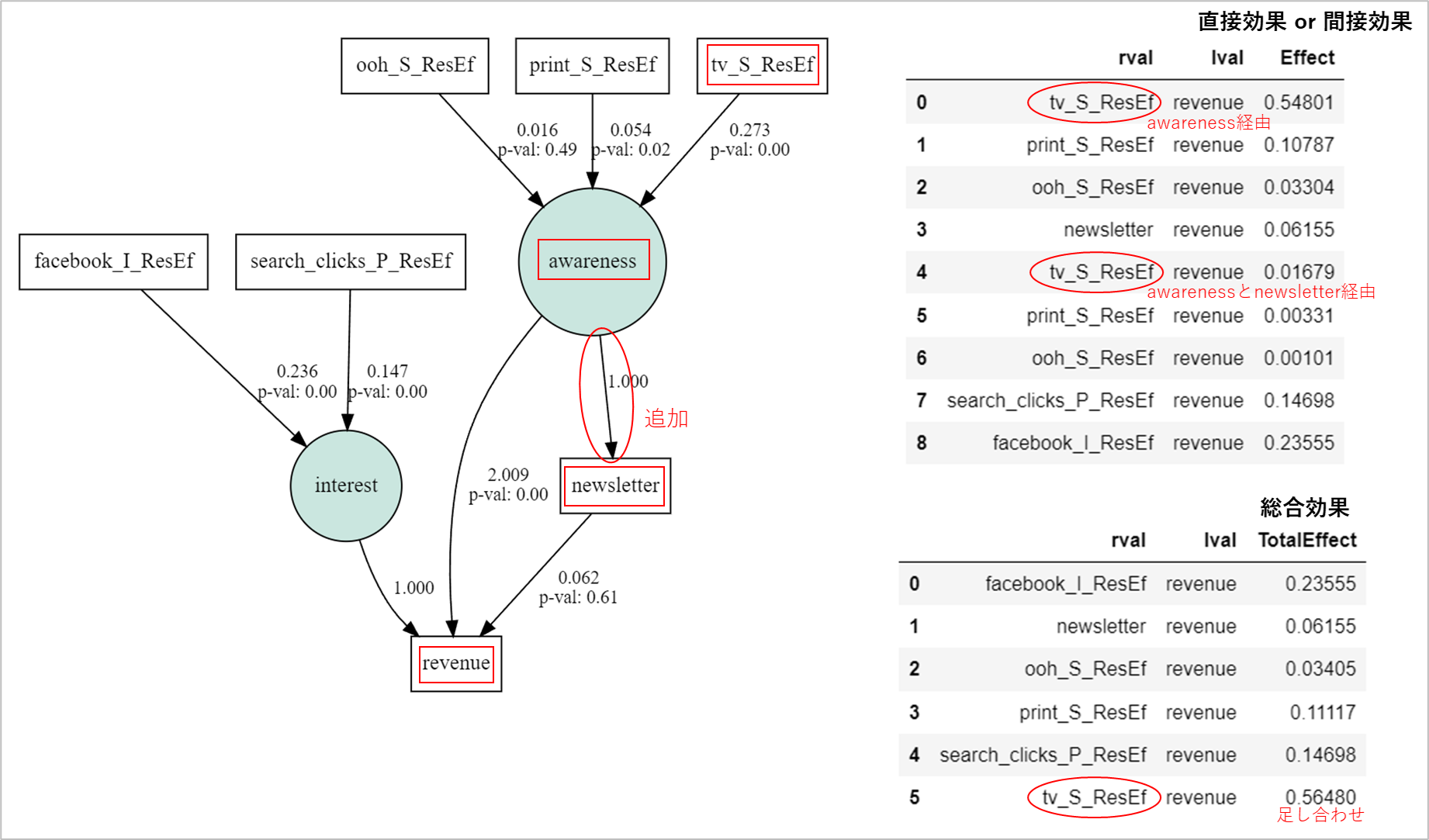
複雑なパス図の時でも処理できるように・・・と思って、ややこしい処理の仕方になってしまったが、なんとか計算できたぞ。
パス係数がAmosと一致していたので、もちろん総合効果もAmosと一致している。
今回のパス図は1変数=1経路で単純なので、複数経路あるときにどういう計算になるか、例も下に載せておく。

(例)

各広告の売り上げへの影響

さて、総合効果もわかったので、各広告の投資額がどの程度売り上げに貢献しているか可視化してみる。
今回のモデルの売り上げに関する予測は、$\sum_{k}^{変数の数}(観測変数_k×総合効果_k$)で表すことができる。つまり、各観測変数が売り上げにどの程度貢献しているか予測値を分解して個別に確認することができる。

以下のように、$\sum_{k}^{変数の数}(観測変数_k×総合効果_k$)の計算を実施して配列として定義する。

# 可視化用のデータ加工
dates = mmmDfResEf_std.DATE.to_numpy() # Date
labels = list(np.sort(mmmDfResEf_std[cols].T.index)) # ラベル名(変数名でソート)
vals = mmmDfResEf_std[cols].T.sort_index().T.to_numpy() # カラムの並びをソートして配列化
coeffi = objcolDf[['rval', 'TotalEffect']].sort_values('rval')['TotalEffect'].to_numpy() # rvalでソートして総合効果を配列化
stacks = (vals*coeffi) # 変数×総合効果
stacks100 = (stacks/stacks.sum(axis=1).reshape(-1,1)) # 変数×総合効果の比率（貢献度）
stacksSum = stacks.sum(axis=1) # 変数×総合効果の合計=売り上げの予測値
print('"dates" shape: ', dates.shape)
print('"labels" length: ', len(labels))
print('"coeffi" shape: ', coeffi.shape)
print('"stacks" shape: ', stacks.shape)
print('"stacks100" shape: ', stacks100.shape)
print('"stacksSum" shape: ', stacksSum.shape)

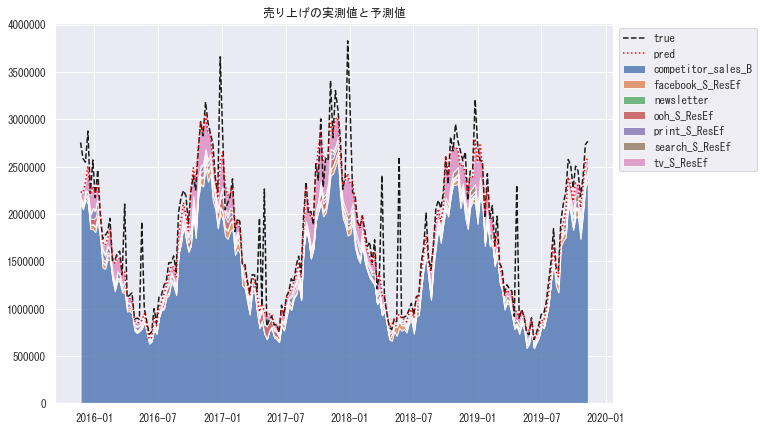
定義したので可視化する。まずは売り上げの実測(黒点線)と予測(赤点線)と、予測の分解した積み上げ面グラフを可視化。

# 可視化
fig = plt.figure(figsize=(10,7))
plt.rcParams['font.family'] = prop.get_name()
# 売り上げの実測値プロット
plt.plot(dates, mmmDfResEf_std.revenue.to_numpy(), label='true', c='k', ls='--')
# 売り上げの予測値プロット
plt.plot(dates, stacksSum
         , label='pred', c='red', ls=':')
# 売り上げの予測値を変数ごとに分解して積み上げ面グラフに
plt.stackplot(dates, stacks.T, labels=labels, alpha=0.8)
plt.legend(loc='upper left', bbox_to_anchor=(1, 1))
plt.title('売り上げの実測値と予測値')
plt.show()

これを見ると、売り上げの多くの部分で業界特有の季節性や盛り上がりによる効果(competitor_sales_B)が効いていると考えられる。
それ以外を見ると、季節性の周期のピークのたびにTV広告への投資効果(ピンクの部分)が大きくなっていることが確認できる。

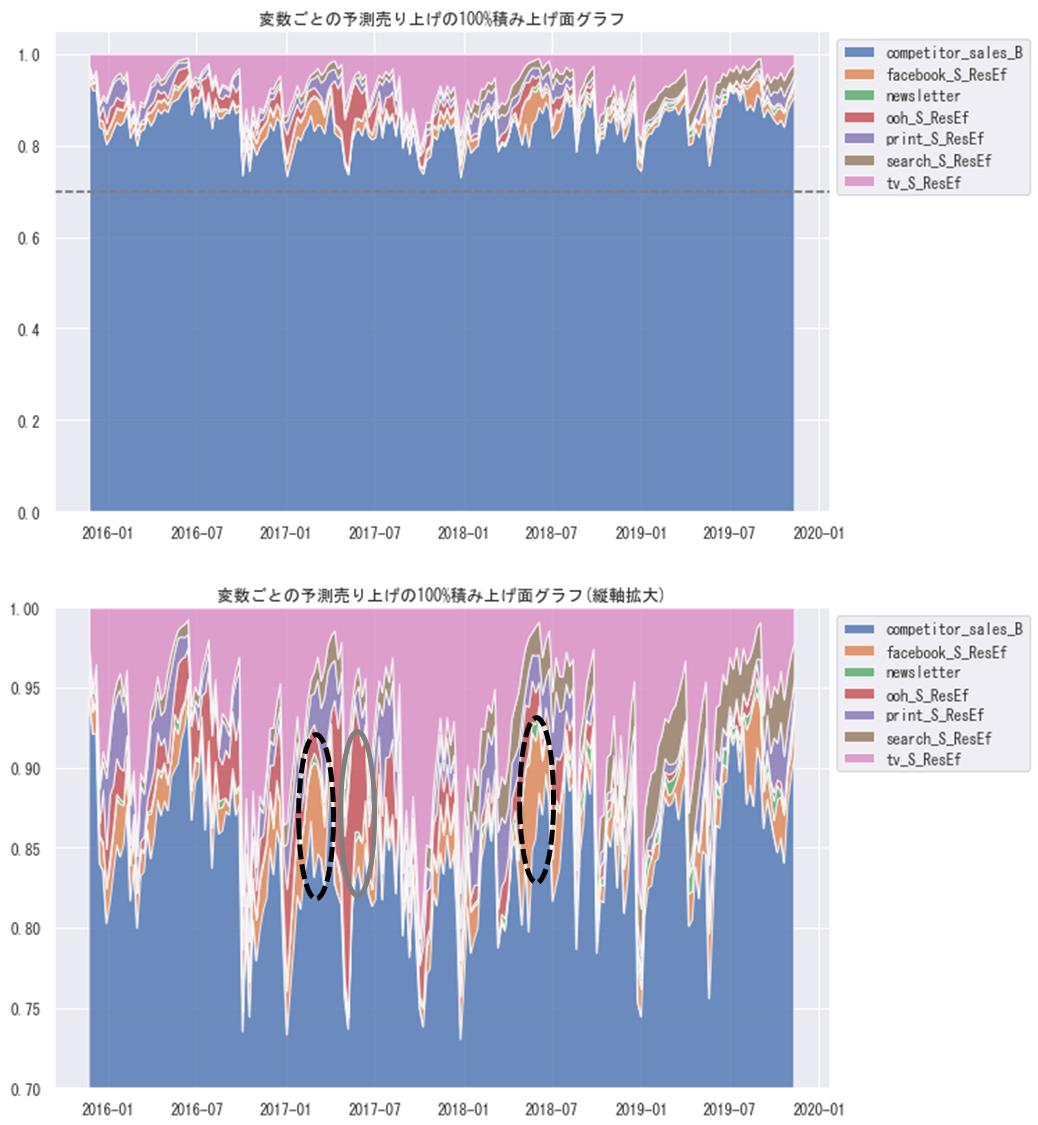
もう少し各変数の貢献度を見るために、100%積み上げ面グラフとして可視化してみる。

# 売り上げの予測値を変数ごとに分解して100%積み上げ面グラフに
fig = plt.figure(figsize=(10,14))
plt.rcParams['font.family'] = prop.get_name()
ax1 = plt.subplot(2,1,1)
ax1.stackplot(dates, stacks100.T, labels=labels, alpha=0.8)
ax1.axhline(y=0.7, c='gray', ls='--')
ax1.legend(loc='upper left', bbox_to_anchor=(1, 1))
ax1.set_title('変数ごとの予測売り上げの100%積み上げ面グラフ')

# 売り上げの予測値を変数ごとに分解して100%積み上げ面グラフに(縦軸拡大)
ax2 = plt.subplot(2,1,2)
ax2.stackplot(dates, stacks100.T, labels=labels, alpha=0.8)
ax2.legend(loc='upper left', bbox_to_anchor=(1, 1))
ax2.set_ylim(0.7, 1)
ax2.set_title('変数ごとの予測売り上げの100%積み上げ面グラフ(縦軸拡大)')
plt.show()

2017年の春前と2018年の夏前の頃(黒点線丸)にfacebookの効果が大きくなり、2017年の夏前の頃(灰色丸)にoohの効果が大きくなっていることなどが確認できる。
実測値のスパイク上に売り上げが伸びている箇所など予測できていないところもあるが、休日のデータを入れると分析の精度も向上するかもしれない。

と、以上のようにsemopyを使って、共分散構造分析を行い、MMMの真似事ができた。
結果もAmosによる結果と相違なかったので、実務でも活用できるライブラリなのではないだろうか。

semopyは多母集団同時分析もできるよ

多母集団同時分析もできる。
lavaanのデータを使って軽くやってみる。csvを作っておく。

#### R ####
library(lavaan)
dat <- HolzingerSwineford1939
write.csv(dat, file = "HolzingerSwineford1939.csv", row.names = TRUE)

読み込み。

#### python ####
import numpy as np
import scipy
import matplotlib as mpl
from matplotlib import pyplot as plt
import matplotlib.font_manager as fm
import seaborn as sns
import pandas as pd
import sklearn
import semopy
import graphviz
jpn_fonts=list(np.sort([ttf for ttf in fm.findSystemFonts() if 'msgothic' in ttf]))
jpn_font=jpn_fonts[0]
prop = fm.FontProperties(fname=jpn_font)
sns.set()
print(semopy.__version__)

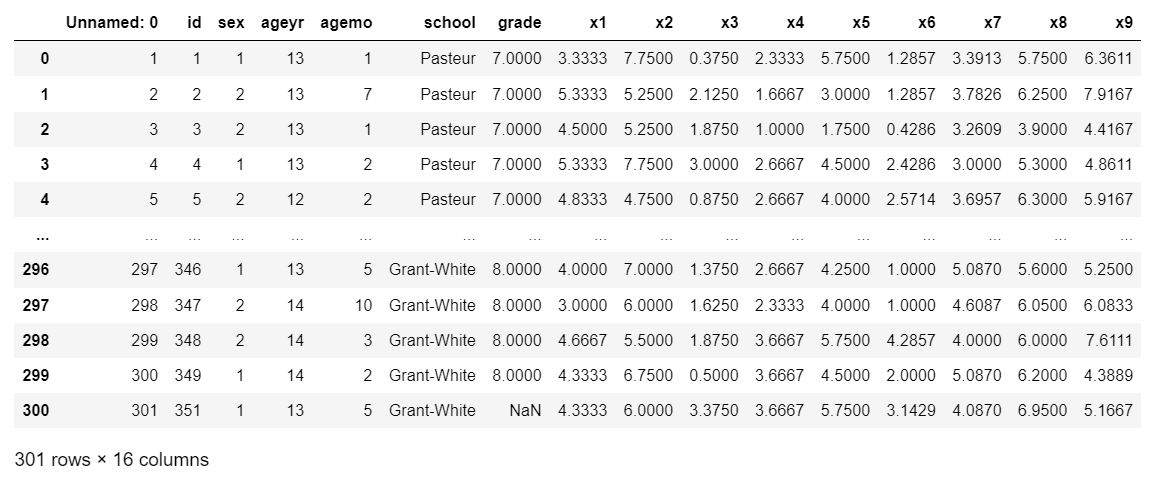
mmmDfResEf_stdGroup = pd.read_csv('HolzingerSwineford1939.csv')
display(mmmDfResEf_stdGroup)

x1~x9が観測変数、schoolが母集団を示している。

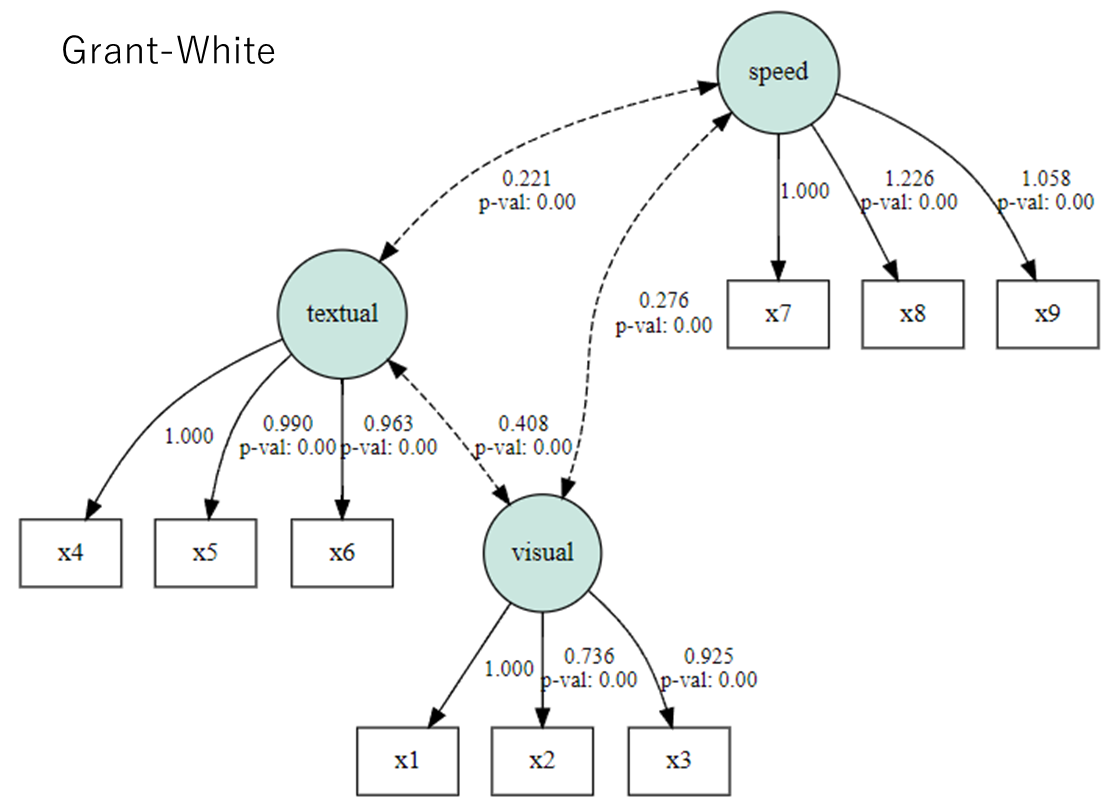
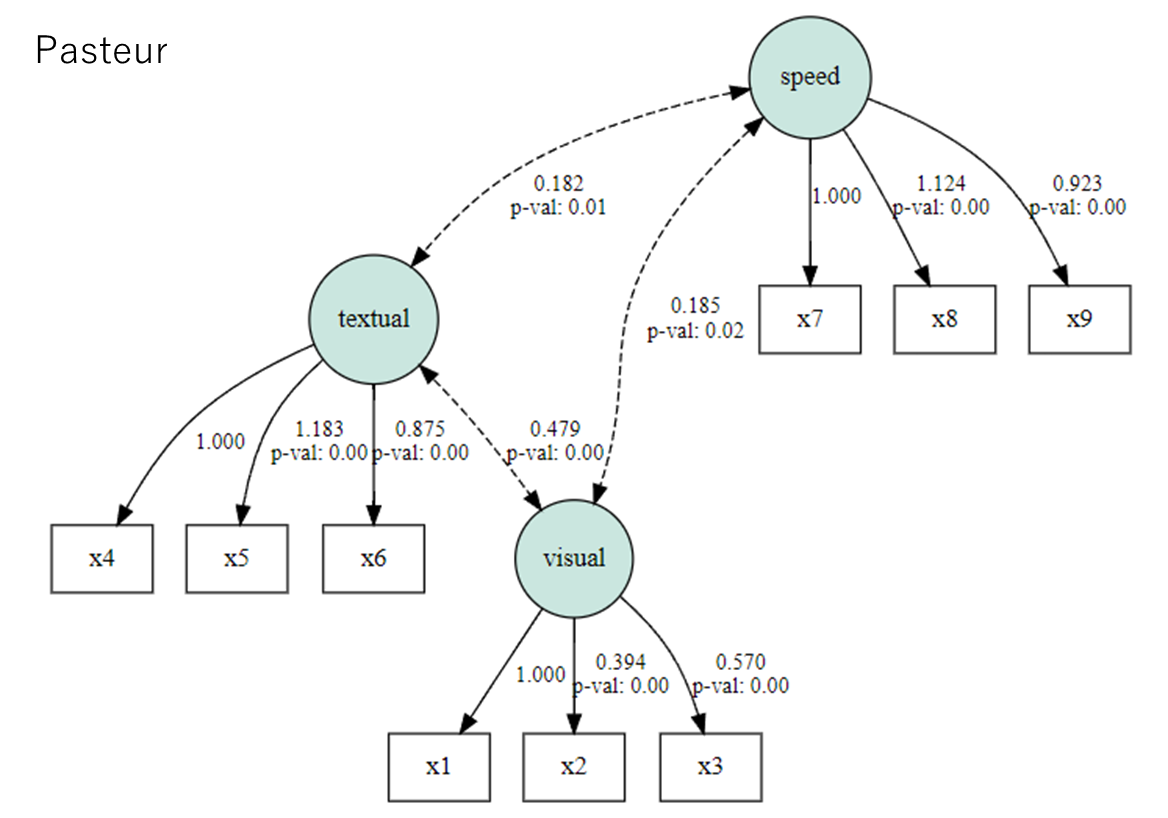
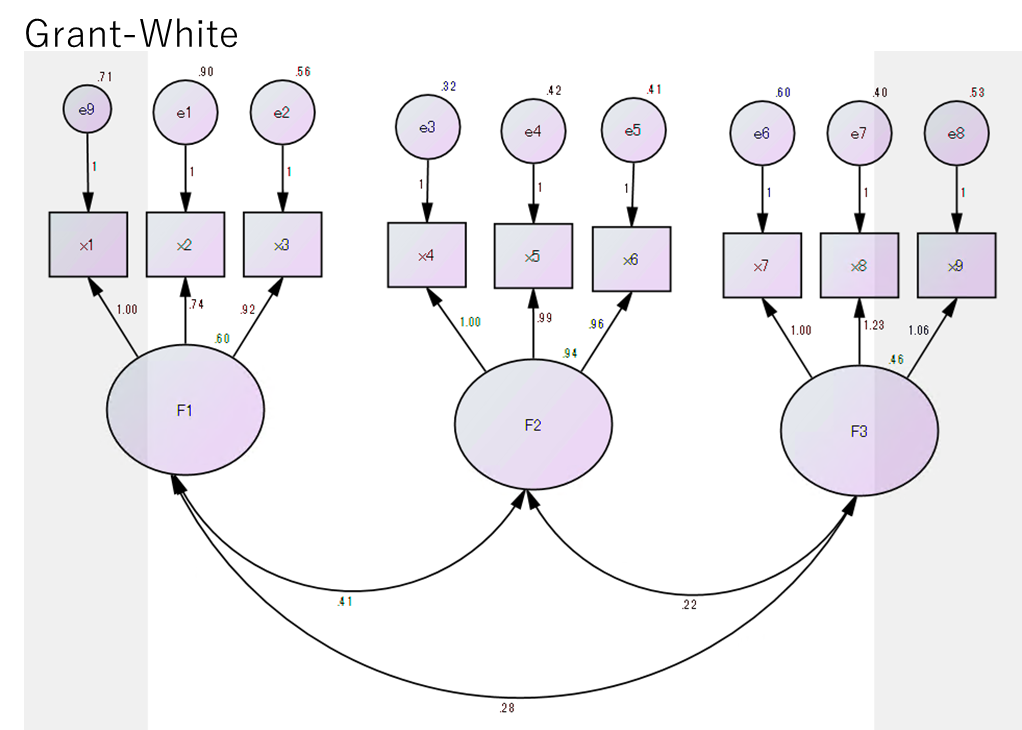
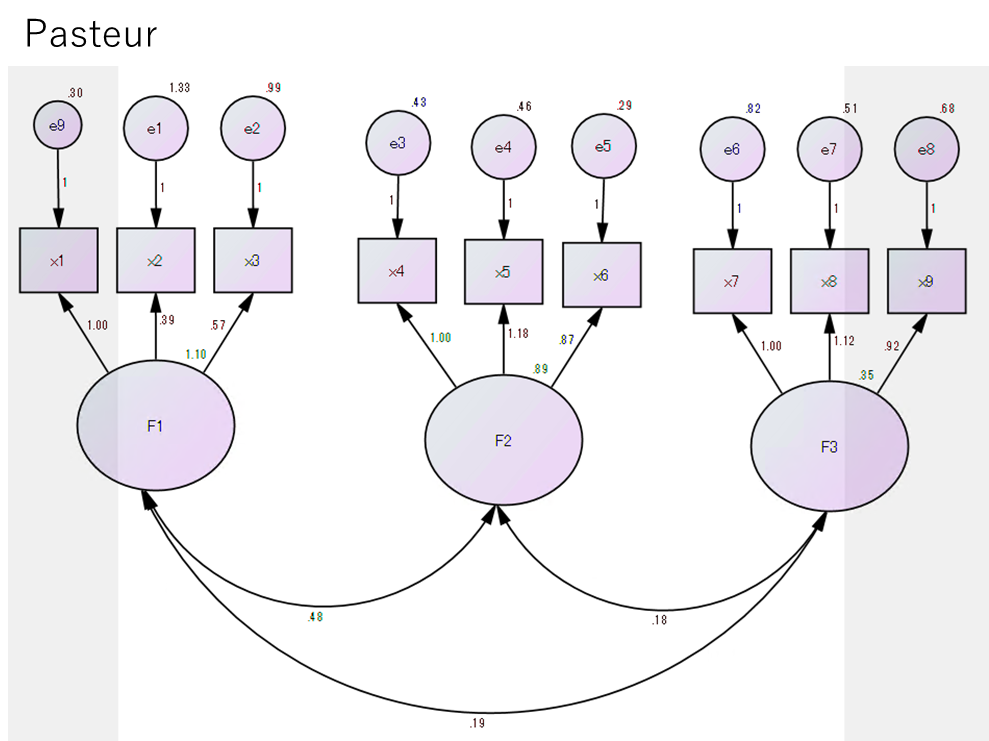
パス図はマルチグーループSEM(多母集団同時分析) 配置不変モデル[Mplus]をそのまま使わせてもらった。

desc = \
'''
visual =~ x1 + x2 + x3
textual =~ x4 + x5 + x6
speed =~ x7 + x8 + x9

visual ~~ textual
visual ~~ speed
textual ~~ speed
'''

多母集団同時分析をするには、multigroup.multigroupを使う。
母集団分の結果が返される。

# パス図、データ、母集団を示す変数、Modelインスタンスを入れる
res = semopy.multigroup.multigroup(desc, mmmDfResEf_stdGroup, 'school', mod=semopy.Model)
# 母集団ごとの結果を確認できる
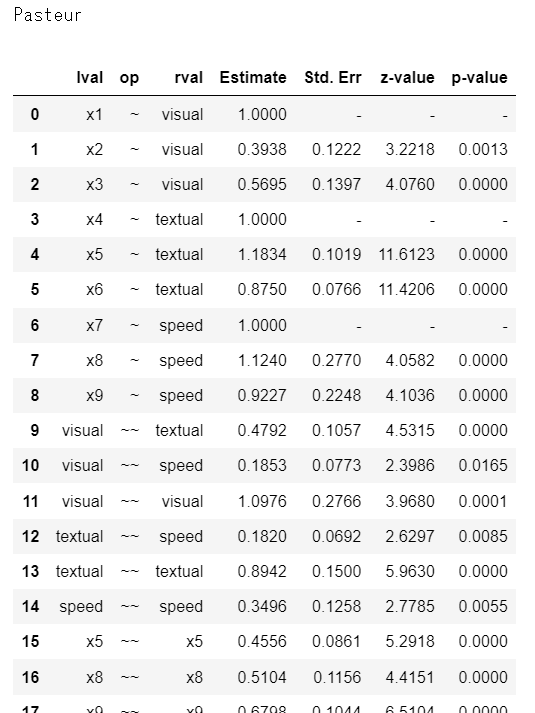
for i in res.estimates.keys():
    print(i)
    inspection = res.estimates[i]
    display(inspection)

母集団Pasteurの結果

母集団Grant-Whiteの結果

しかし、なんとmultigroupの戻り値ではsemopy標準のsemplotが使えなくて困った…。母集団ごとのパス図を可視化できない…。
なので、semopyのgitlabのplot.pyを参考に、可視化する関数を定義した。

# multigroupのres.estimatesの結果をパス図として可視化する関数
def mySemplot(inspection, obs_cols, filename: str, plot_covs=False
              , plot_exos=True, engine='dot', latshape='circle'
              , plot_ests=True, std_ests=False, show=False):
    all_vars = np.unique(inspection.lval.to_list()+inspection.rval.to_list())
    exVar = [i for i in all_vars if i not in obs_cols]
    inVar = [i for i in all_vars if i in obs_cols]

    g = graphviz.Digraph('G', engine=engine)
    g.attr(overlap='scale', splines='true')
    g.attr('edge', fontsize='12')
    g.attr('node', shape=latshape, fillcolor='#cae6df', style='filled')

    for lat in exVar:
        g.node(lat, label=lat)

    g.attr('node', shape='box', style='')

    for obs in inVar:
        g.node(obs, label=obs)

    regr = inspection[inspection['op'] == '~']
    
    #try:
    #    exo_vars = mod.vars['observed_exogenous']
    #except KeyError:
    #    exo_vars = set()

    exo_vars = set()
    for _, row in regr.iterrows():
        lval, rval, est = row['lval'], row['rval'], row['Estimate']
        if (rval not in all_vars) or (~plot_exos and rval in exo_vars) or\
            (rval == '1'):
            continue
        if plot_ests:
            pval = row['p-value']
            label = '{:.3f}'.format(float(est))
            if pval !='-':
                label += r'\np-val: {:.2f}'.format(float(pval))
        else:
            label = str()
        g.edge(rval, lval, label=label)

    if plot_covs:
        covs = inspection[inspection['op'] == '~~']
        for _, row in covs.iterrows():
            lval, rval, est = row['lval'], row['rval'], row['Estimate']
            if lval == rval:
                continue
            if plot_ests:
                pval = row['p-value']
                label = '{:.3f}'.format(float(est))
                if pval !='-':
                    label += r'\np-val: {:.2f}'.format(float(pval))
            else:
                label = str()
            g.edge(rval, lval, label=label, dir='both', style='dashed')
    g.render(filename, view=show)
    return g

# パス図可視化
obs_cols = mmmDfResEf_stdGroup.columns.to_numpy() # 母集団名リスト
for i in res.estimates.keys():
    print(i)
    inspection = res.estimates[i]
    g = mySemplot(inspection, obs_cols, "tmp.png", plot_covs=True)#, engine='circo')
    display(g)

Amosによる多母集団同時分析の結果は以下。

はい、ということで結果が一致していた。
多母集団同時分析をする時も、semopyでできそう。

おわりに

semopyの検証をした。共分散構造分析のプロからしたら、足りないところもあるのかもしれないけど、実務で活用することはできそうだという所感。
素人の自分が強いて文句を言うなら、固定母数の設定の仕方がわからなかった。
Amosみたいに自由に設定できたらいいんだけどどうすればよかったんだろう。
多分、方程式を記述するところでSTART(v), BOUND(l, r), CONSTRAINT(constr)などを設定すればよかったのかな。あまり論文を読み切れていなくて不明。
でも良いツールだと思いました(小並感)。

以上！