はじめに
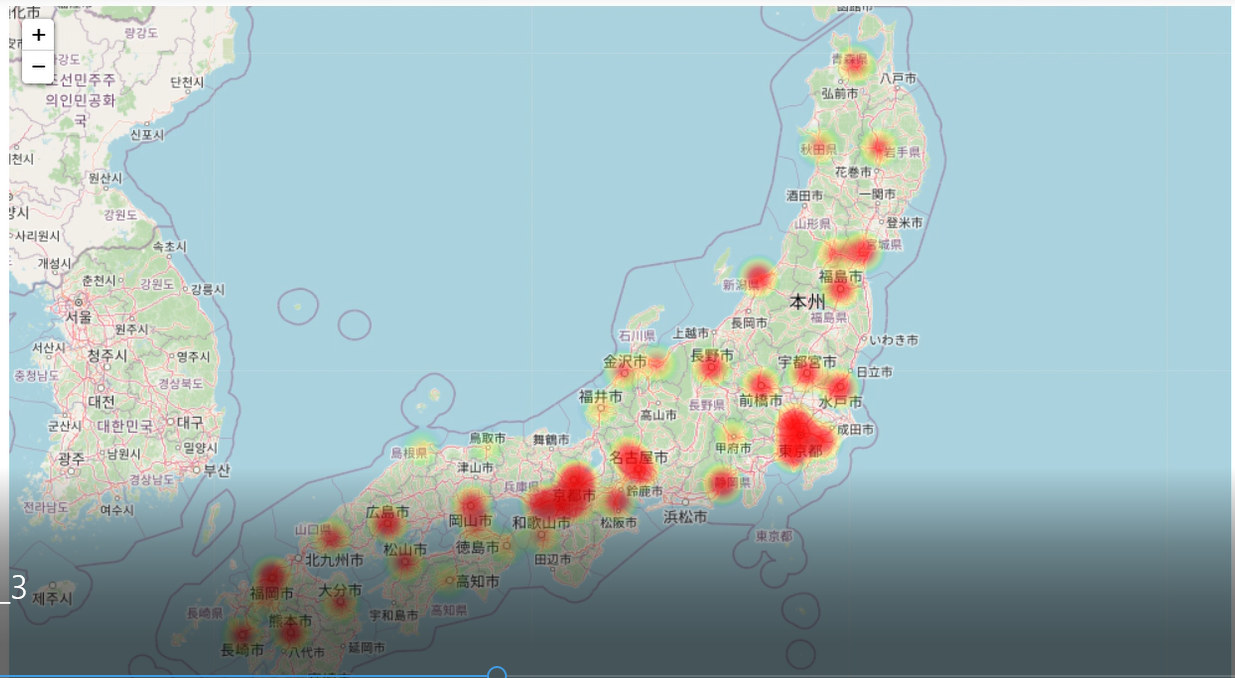
PythonでSIRモデルを用いてCOVID-19の感染拡大シミュレーションを行いました. モデルについては47都道府県それぞれ作成し, ヒートマップでの可視化を行いました.
github ページ
https://github.com/chihina/analysis_covid_19_python
可視化動画 (フリーソフトでの編集のため若干の透かしが入っています. ごめんなさい!!)
https://www.youtube.com/watch?v=7XvPKcasL1U
開発環境
インタプリタ: python 3.71
特殊なライブラリ: folium==0.11.0
その他 matplotlib, numpyなどです.
SIRモデルについて
SIRモデルの常微分方程式は以下のようなものです.
(簡単にいうと βは感染率, γは回復率を表します)
\frac{dS}{dt}(t) = -\beta S(t)I(t)\\
\frac{dI}{dt}(t) = \beta S(t)I(t) - \gamma I(t)\\
\frac{dR}{dt}(t) = \gamma I(t)\\
S (susceptible)... 感受性保持者(感染する可能性がある人)
I (Infected)... 感染者
R (Recovered)... 免疫保持者(もしくは隔離者)
1つ目の方程式
\frac{dS}{dt}(t) = -\beta S(t)I(t)\\
左辺は, 単位時間あたりの感受性保持者の変化率を表します. 感受性保持者と免疫保持者に感染率を掛け合わせることでこれを表現します.
つまり, 単位時間あたりに感染した人の分だけ S が減少するということです.
2つ目の方程式
\frac{dI}{dt}(t) = \beta S(t)I(t) - \gamma I(t)\\
左辺は, 単位時間あたりの感染者の変化率を示します.
右辺第一項は先程登場したものです. 右辺第二項については, 単位時間あたりに回復する人を示します.
つまり, 単位時間あたりに感染する人から回復する人を引いたものということです.
3つ目の方程式
\frac{dR}{dt}(t) = \gamma I(t)\\
左辺は, 単位時間あたりの免疫保持者の変化率を示します. 右辺は先程のものと同様で, 単位時間あたりに回復する人を示します.
つまり, 単位時間あたりに回復する人の分だけRが増加するということです.
SIRモデルの改良
ここまで述べてきたSIRモデルを47都道府県分考えたところで, 1つずつが独立してしまうために意味がありません. よって, 人口比データを用いて他の都道府県の感染状況による影響項を追加しました.
\frac{dS}{dt}(t) = -\beta S(t)I(t) - I_{pref} × PR_{pref} × 0.1\\
\frac{dI}{dt}(t) = \beta S(t)I(t) - \gamma I(t) + I_{pref} × PR_{pref} × 0.1 \\
\frac{dR}{dt}(t) = \gamma I(t)\\
追加した項について
I_{pref} × PR_{pref} × 0.1
1つ目の文字はその時考えている県以外の感染者の状況を表現しています.
2つ目の文字は, その時考えている県の東京都の人口比を示します.
よって, この項によって他の都道府県で感染者が増えれば自身の県でも感染者が増加するようにしています. 人口比の情報を使用したことで東京都, 大阪府, 愛知県など人口が多い県の影響が強くなるようにしています.
実装方法
以上で改良したSIRモデルを, pythonで解いていきます. 本来ならばscipyを使用すれば簡単に実装できますが, 理解のために地道に実装しました. 詳しくはコードをご覧の上, ご質問お願いします!!
実装手法: 4次のルンゲクッタ法
ルンゲクッタ法については説明がたくさんありますので, 「4次のルンゲクッタ法」で検索をお願いします.
可視化方法
python foliumで時系列ヒートマップ(time series heatmap)描く
https://sammi-baba.hatenablog.com/entry/2018/12/25/074017
を参考にさせていただきました. 都道府県ごとの感染者情報をpandasのdataframeで作成後,
csvに書き出したものを読み込み使用しました. 実際の動画はyoutubeにアップロードしたのでご覧ください!!
可視化動画 (フリーソフトでの編集のため若干の透かしが入っています. ごめんなさい!!)
https://www.youtube.com/watch?v=7XvPKcasL1U
まとめ
完璧に今の感染状況をつかむことはできませんでしたが, 比較的単純な常微分方程式を持って
ある程度の感染拡大の再現ができたことは非常に驚きでした.
より詳細な内容について質問等ございましたらぜひお願い致します!!
参考文献
以下の記事, 統計データを参考にさせていただきました.
ありがとうございます.
[1] python foliumで時系列ヒートマップ(time series heatmap)描く
https://sammi-baba.hatenablog.com/entry/2018/12/25/074017
[2] 人口推計 平成29年10月1日現在人口推計 国勢調査サイト(e-stat)
https://www.e-stat.go.jp/dbview?sid=0003215844
[3] Data of Japan githubページ (2020年 7月 28日アクセス)
https://www.e-stat.go.jp/dbview?sid=0003215844