はじめに
この記事はフィボナッチ数列の計算を通して計算の工夫の重要性を学んだためメモとして投稿します.
フィボナッチ数列とは?
An = An-1 + An-2 (A0 = A1 = 1)の式で表される数列です.
1 1 2 3 5 8 .... と自身の前の2項を足したものが項となる数列です.
実装(再帰, メモ化再帰, 動的計画法)
まず, 再帰で実装
pythonにてフィボナッチ数列の任意の項を求める関数を実装しました.
def fib(n):
if n == 0 or n == 1:
return 1
return fib(n-1) + fib(n-2)
この関数により, 任意のフィボナッチ数列の項が求められます.
しかし, この関数では計算量が大きいです.
fib(5)を求めるためにはfib(4)とfib(3)を求めます.
fib(4)を求めるときはfib(3)とfib(2)を求めます.
この場合においてfib(3)は2回計算されます.
このように再帰での実装では無駄な計算が生じてしまいます.
メモ化再帰での実装
メモ化再帰では通常の再帰に加えて, 計算した項の情報を保持します.
今回はpythonの辞書型の構造を用います.
class Fib_memo:
def __init__(self):
self.fib_memo = {}
def cal_fib(self, n):
if n == 0 or n == 1:
self.fib_memo[n] = 1
return 1
#既に計算した項なら保存した情報を使う
if n in self.fib_memo.keys():
return self.fib_memo[n]
self.fib_memo[n] = self.cal_fib(n-1) + self.cal_fib(n-2)
return self.fib_memo[n]
既に計算した項を保存して置き, それを用いることで計算の無駄が省けています.
動的計画法での実装
動的計画法では, フィボナッチ数列の項を小さい方から計算することで
計算の無駄を省いています.
def fib_dynamic(n):
# 結果を保持する辞書
cal_result = {}
# 初期値の設定
cal_result[0] = 1
cal_result[1] = 1
if n == 0 or n == 1:
return 1
for i in range(2, n+1):
cal_result[i] = cal_result[i-1] + cal_result[i-2]
return cal_result[n]
検証
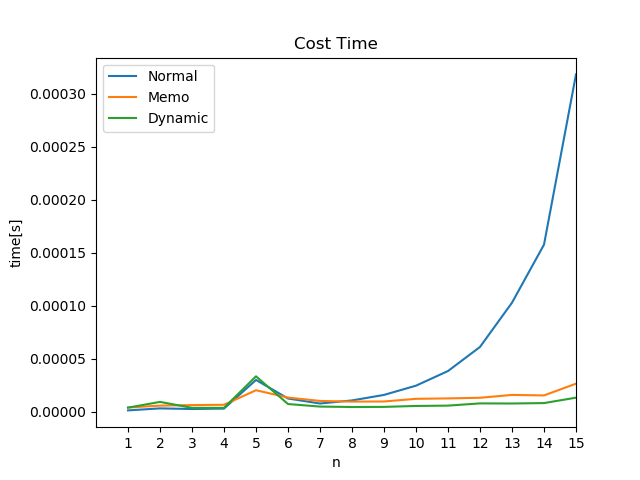
n = 1 ~ 15 で 3つの実装についての実行コスト(秒)を計算しました.
結果のグラフを以下に示します.
Normalが通常の再帰, Memoがメモ化再帰, Dynamic が 動的計画法 です.
グラフより, n = 10 くらいから実行速度について大きな差が出てくることがわかります.
結論
以上より, 簡単な工夫で実行速度が大きく異なることがわかりました.
普段は実行速度についてあまり意識することもなく, 重要性もわかりにくいです.
今回の結果から重い計算においては, データ構造とアルゴリズムの工夫が必須であると感じました.