フォノン
フォノンとは格子振動を量子化したものである。
運動エネルギーが大きい物質は早い速度で運動しているだろう。同じ重さの物質の運動エネルギーの大小を比較したければ、速度を比較すればいいわけだ。では、温度が異なる物質同士の持っているエネルギーの違いは何を比較すれば良いのだろうか。温度が高い物質は加熱されることで得た熱エネルギーをなんらかの形で物質中に取り込んでいるはずだ。それこそが熱振動である。温度が高い物質は、温度が低い物質に比べて構成粒子の原子や分子が激しく振動しているのだ。
さて、熱エネルルギーは温度が高いところから低いところへと移動する。これは、熱振動が結晶格子を伝播していく過程とみなせる。格子振動の伝搬は波のような性質を持つであろうが、量子物理学において電磁波の波である光をフォトンの粒子として考えることができるのと同じように、格子振動の伝搬もフォノンの粒子として考えられるだろう。
なにやら難しいことを書いてはみましたが、原子レベルの熱エネルギーの移動とかを考えるときはフォノンについて考えれば良いってことなのでしょう。実際、フォノンの平均速度$ v$と平均自由工程$ l$を用いると物質の熱拡散率$ \alpha$は次のような非常に簡単な関係式で表されます。
$ \alpha = \frac{1}{3} v l$
とても美しいですね。$ v$と$ l$が分かると物質全体の熱物性が分かるのだ。フォノンって分かると便利なんですね。この式についての導出は省略いたします。キッテルを参照してください。
・Charles Kittel著、宇野良清 津屋昇 新関駒二郎 森田章 山下次郎 共訳「キッテル固体物理学入門」第8版、丸善出版、2015
フォノンの分散関係
物質中のフォノンの挙動を理解するにはなにが分かればいいのでしょうか。結局は波なので波数$ K$に対する分散関係$ \omega$の関係式を導出すれば良い。この関係式を次に示す。これも詳細はキッテルをご参照ください。
$ \omega^2 = \frac{4 C}{M} \sin^2(\frac{1}{2}K a)$
質量Mの原子が間隔$a$で一列に並んだときのフォノンの分散関係が上の式である。$ C$は原子間のバネ定数である。
ここから$ v$の方は比較的簡単に計算ができて、分散関係の波数の微分値が群速度$ v$となる。
$ v = \frac{d \omega}{d K}$
プロットしよう
プロットしてみましょう。扱っている内容は難しいが、プロット自体は簡単である。
import matplotlib.pyplot as plt
import numpy as np
C = 1
M = 12
a = 2
K = np.linspace(-2*np.pi/a, 2*np.pi/a, 10000)
omega = np.abs(np.sqrt((4*C/M))*np.sin(0.5*K*a))
fig = plt.figure()
ax = fig.add_subplot(111)
plt.plot(K,omega)
ax.set_xlabel('K', fontsize=20, color='black')
ax.set_ylabel('$\omega$', fontsize=20, color='black')
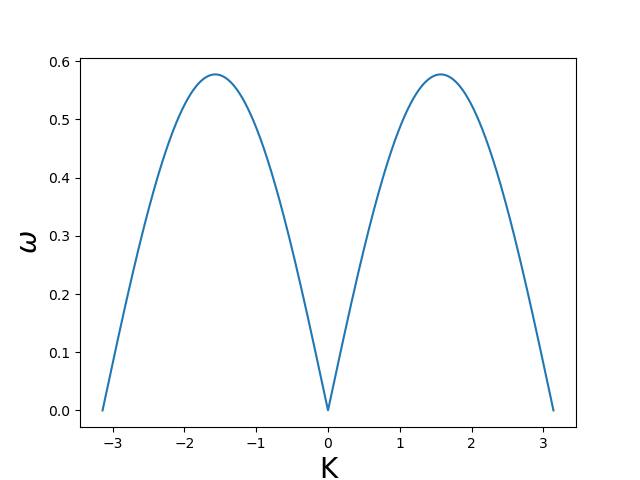
今回は$C = 1$, $M = 12$, $a = 2$として、$K$が$- \frac{2 \pi}{a}$から$\frac{2 \pi}{a}$の範囲でプロットしている。実行結果がこちらです。
うん、いい感じです。
値は物理的に意味のある正の値のみを採用しているので$ \omega$の周期は$\frac{2 \pi}{a}$となります。今回、$K$の描画範囲は$- \frac{2 \pi}{a}$から$\frac{2 \pi}{a}$としていますので2周期分プロットしてます。さっきの式からこの傾きが群速度になるのだということがわかります。$K = 0$付近の群速度が最速で、$K = \pm \frac{\pi}{a}$の群速度が最低速度ということになるのかと思います。
フォノンの分散関係がわかったところで物性との関係をつけるのは難しいですが、とりあえず今日のところは分散関係がプロットできたので良しとします。