なぜ私たちはいつも締め切りに追われるのか
みなさんはいつも締め切りに追われていますか?僕は追われています。
私たちがいつも締め切りに追われる理由を、研究者の立場から考察した論文があります。それは、AI研究の第一人者である東京大学の松尾豊教授が、2006年に人工知能学会論文誌へ投稿した論文です。その論文では、人間の集中力と仕事量の関係をモデル化し、それに対する締め切りの影響を検討することで、私たちがいつも締め切りに追われる理由を考察しています。
論文中では、集中力と仕事量の関係のモデルをリソース分配モデルと呼び、最大の仕事を与える集中力の関数を最適化問題の最適解として求めています。ここでは、論文の内容をまとめた後に、リソース分配モデルの数値解をPythonのscipyで求めます。
松尾教授の論文は公開されているので、ご興味があれば、ぜひご一読ください。
論文の要約1
私たちがいつも締め切りに追われる理由を考えるにあたって、まず、一般的に仕事をいかにこなしていけば良いかをモデル化して考えます。
リソース分配モデルの定式化
時間$t=[0,T]$の間に実施できる仕事$W$について考えます。まず、仕事の効率$u$は、集中力$r(t)$の関数であるとします。この、集中力にいろいろ条件を加えます。人間にはやる気が出る時とやる気が出ない時とがあるので、$r(t)$は時間に依存する関数とします。また、人間の集中力には限度があるので、最大値$r_{max}$があるとします。そして、時間$t=[0,T]$の間の集中力の合計は一定値$R$であるとします。これを、式にすると次のようになります。
\begin{aligned}
0 < r(t) < r_{max}\\
\int_0^T{r(t)}dt = R
\end{aligned}
ここで、仕事の効率の関数を単純化して次のように定義します。
u(r(t)) = r(t)^k
$u$の積分$W$とした時、仕事をいかにこなしていけば良いかというのは、最大の$W$を与える$r(t)$を求める最適化問題となります。
\begin{aligned}
{\rm maximize}\quad & W = \int_0^T{u(r(t))}dt=\int_0^T{r(t)^k}dt \\
{\rm subject\ to}\quad & 0 < r(t) < r_{max} \\
& \int_0^T{r(t)}dt = R
\end{aligned}
最適化問題の目的関数、決定変数、制約条件がそれぞれ$W$、$r(t)$、${\rm subject\ to}$以下、となります。
リソース分配モデルの最適解
論文では、リソース分配モデルの最適解として次の式が示されています。
(1)$0 < k \leq 1$
$$r(t) = \frac{R}{T}$$
この時、$W = \int_0^T{(\frac{R}{T})^k}dt = R(\frac{R}{T})^{k-1}$
(2)$1 > k$
\begin{aligned}
r(t) =
\begin{cases}
r_{max} \quad & (0 \leq t < \frac{R}{r_{max}})\\
0 \quad & (\frac{R}{r_{max}} \leq t \leq T)
\end{cases}
\end{aligned}
この時、$W = \int_0^{\frac{R}{r_{max}}}{(r_{max})^k}dt = R(r_{max})^{k-1}$
ここで$u(r(t)) = r(t)^k$より、$0 < k \leq 1$の仕事は集中力を2倍にしても効率が2倍にならない仕事で、論文中ではやっつけ仕事と呼んでいます。やっつけ仕事の時の最適解は$r(t) = \frac{R}{T}$であることから、集中力は小さくても良いので持続させることが最大の仕事に繋がることがわかります。逆に、$1<k$の仕事は集中力を2倍すると効率が2倍以上になる仕事で、論文中では創造的仕事と呼んでいます。創造的仕事の場合は、短期間に集中して取り組むことが最大の仕事に繋がります。
なぜ私たちはいつも締め切りに追われるのか
結論を先に言います。創造的仕事の場合、締め切りに追われいつも以上に集中して取り組めばいつも以上に仕事の効率が上がり結果間に合うことがあるからです。論文中での”私たち”は研究者を指しています。研究者の仕事は創造的仕事なので、締め切りに追われ集中力を上げたことで、なんとか間に合う経験を積み重ねた結果、「計画をたてて余裕をもってやる」ということが学習できないと考察しています。一方、やっつけ仕事の場合にはどう足掻いても間に合わない仕事は間に合いません。
これをリソース分配モデルから導きます2。締め切りに追われるということを表すために、$t$の最大値を$T$から$\frac{T}{s}$にします。ここで、$s>1$とします。締め切りに追われた結果、我々は集中力の限界を突破し、$r(t)$の最大値が$r_{max}$から$sr_{max}$となったとします。ここでも、時間$t=[0,\frac{T}{s}]$の間の集中力の合計は一定値$R$とします。以上をまとめると、締め切りに追われた条件下でのリソース分配モデルは次のようになります。
\begin{aligned}
{\rm maximize}\quad & W' =\int_0^{T/s}{r'(t)^k}dt \\
{\rm subject\ to}\quad & 0 < r'(t) < sr_{max} \\
& \int_0^{T/s}{r'(t)}dt = R
\end{aligned}
ここで、$r'(t)$、$W'$はそれぞれ、締め切りに追われた条件下での集中力と仕事です。締め切りに追われた条件下でのリソース分配モデルも、先ほどとの対応から、次のような関数が最適解になると考えられます。以下、締め切りに追われていない時の仕事を$W_0$と置きます。
(1)$0 < k \leq 1$
$$r'(t) = \frac{R}{T/s}$$
この時、$W' = \int_0^{T/s}{(\frac{R}{T/s})^k}dt = s^{k-1}R(\frac{R}{T})^{k-1} = s^{k-1} W_{0}$
ここで、$s>1$かつ$0 < k \leq 1$より$W'< W_0$
(2)$1 > k$
\begin{aligned}
r'(t) =
\begin{cases}
s r_{max} \quad & (0 \leq t < \frac{R}{s r_{max}})\\
0 \quad & (\frac{R}{s r_{max}} \leq t \leq T/s)
\end{cases}
\end{aligned}
この時、$W' = \int_0^{\frac{R}{s r_{max}}}{(s r_{max})^k}dt = s^{k-1}R(r_{max})^{k-1} = s^{k-1} W_{0} $
ここで、$s>1$かつ$k > 1$より$W' > W_0$
締め切り$t = T/s$までに終わらせないといけない仕事を$W_{task}$とします。仕事には既に追われているので$W_{task} > W_0$です。$0 < k \leq 1$のやっつけ仕事の時は、$W'< W_0 < W_{task}$が成り立つので、どう足掻いても締め切りには間に合いません。一方で、$k > 1$の創造的仕事の時は、$W'$と$W_{task}$は共に$W_0$より大きいので、締め切りに迫られて集中力が増大した結果、間に合う可能性があります。こうして、間に合ってしまうばっかりに、計画的に仕事を進めることを学習できません。
scipyによるリソース分配モデルの解析
以上、私たちがいつも締め切りに追われる理由がわかりましたね。それでは、このリソース分配モデルをscipyを使って解いていきます。以下、リソース分配モデルを解いて結果を図示するプログラムです。今回は、$r_{max}=15$、$R=45$、$T$が10ステップの条件で、$k$を0.1から10まで飛び飛びに変化させて$r(t)$をプロットします。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from scipy.optimize import minimize
def objective_function(r, k):
return -np.sum(np.power(r, k)) # 目的関数を定義して最大化するために符号を反転
def constraint(r, T, R):
return np.sum(r) - R # 制約条件 ∫[0,T] r(t) dt = R
def r_maximize(k, s, T, R):
initial_guess = 12 # 初期推測
bounds = [(0, r_max)] * T # r(t) が 0 から r_max の間にあることを示す制約
# 最適化を実行
result = minimize(objective_function, initial_guess, args=(k,), constraints={'type': 'eq', 'fun': constraint, 'args': (T, R)}, bounds=bounds)
return result.x
# パラメータの設定
k_vec = [0.1, 1, 5, 9.5, 10]
r_max = 15
T = 10
R = 3*r_max
# グラフの描画と最適化
fig = plt.figure()
ax = fig.add_subplot(111)
colors = []
merkers = ['--o', '--^', '--s', '--D', '--+']
for color_i in range(len(k_vec)):
colors.append(cm.coolwarm(color_i/len(k_vec)))
for i in range(len(k_vec)):
optimal_r = r_maximize(k_vec[i], r_max, T, R)
plt.plot(optimal_r/r_max, merkers[i], label=str("k =" + str(k_vec[i])), markeredgewidth=0.75, markeredgecolor="k")
ax.set_xlabel('t', fontsize=20, color='black')
ax.set_ylabel('$r(t)/r_{max}$', fontsize=20, color='black')
plt.legend(frameon=False)
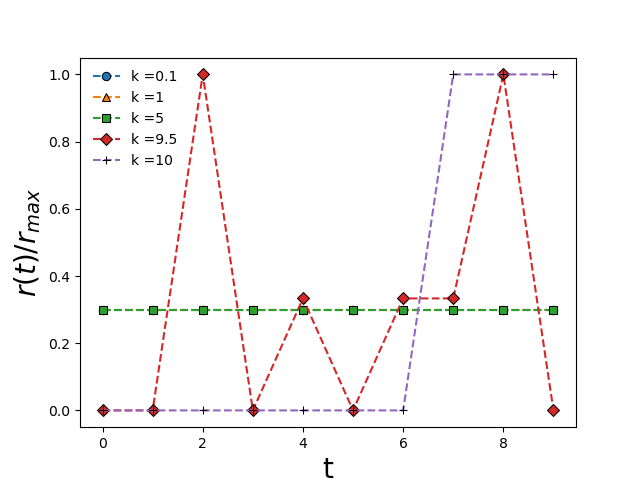
プログラムによって得られた結果を示します。グラフの横軸が時間で縦軸が$r_{max}$
で規格化された$r(t)$です。設定条件から$\frac{R}{T} = 0.3$となります。
scipyで得られた数値解析では論文で示された解析解と少し異なる結果が得られました。まず、$k = 0.1, 1, 5$において$r(t) = 0.3 = \frac{R}{T}$となりました。また、$k = 10$において$r(t) = r_{max}$または$0$となりました。そして、$k = 9.5$において、それらの中間の振る舞いが見られました。
まず、論文と一致している点について述べます。$0 < k \leq 1$において$r(t) = \frac{R}{T}$が得られました。また、$k$が十分大きい時、$r(t) = r_{max}$または$0$となりました。論文では$r(t) = r_{max}$となる範囲は$0 \leq t < \frac{R}{r_{max}}$としていましたが、実際は範囲の指定はなく$k = 10$の結果は論文での解析解と一致します。従って、$0 < k \leq 1$のやっつけ仕事では、大きくなくとも集中力を持続させることがよく、$k$が十分大きい創造的仕事では、短期間に集中して取り組むことが良いです。全体の傾向は、scipyの数値解と論文の解析解が一致したと言っていいと思います。
scipyで得られた数値解析ではその中間が解析解と異なります。まず、$k>1$で創造的な仕事になるはずが、$k = 5$においても$r(t) = 0.3 = \frac{R}{T}$でした。また、$k = 9.5$において、$r(t) = r_{max}$または$0$以外の値が現れました。scipyで得られる最適解は初期条件に依存せて大幅に変わったりするので、ちゃんと解析解と一致させるためには初期条件をよく検討しなくてはいけない気がします。
まとめ
「なぜ私たちはいつも締め切りに追われるのか」のリソース分配モデルについて解説し、これをscipyで解いてみました。scipyの数値解析は完全には解析解と一致しませんでしたが、概ね傾向はあってたのでおよそ解けてると思います。リソース分配モデルは、$u(r(t)) = r(t)^k$の妥当性や$k$の見積り方など、論文では検討つくされていない、さらなる改善も考えられます。しかし、単純なモデルでありながら、得られる結論が明快で面白いことに意義があると思います。以上です。