席替え問題による整数計画問題入門(pulp)

こんにちは。
今日は席替え問題を通じて整数計画問題やpulpの基礎的な内容について紹介したいと思います。

整数計画問題とは最適化問題の解が整数である制約を入れているものになります。

今日は席替え問題と僕が勝手に名付けた問題を用いて整数計画問題について説明します。

席替え問題とは決められた席数の中で各々の人がそれぞれの席に対して希望度を持っていて、全体の希望をなるべく満たすような席替えを決めるという問題です。
図で考えると以下のようになります。

定式化

数学的に定式化していきます。

生徒$i$は席数次元の希望度ベクトル$W_i$を持っています。
生徒$i$の座席の所属を表すベクトルを$x_i$で定義し、座席$j$に座るならば１、座らないならば０が入るベクトルです。この$x_i$が求める変数になります。

生徒集合を$I$で、座席集合を$S$で定義します。

目的関数は、$\displaystyle \sum_{i \in I} {W_i}^t x_i$になります。全体の希望度を最大化したいのでこの目的関数を最大化します。

制約を入れて行きます。

制約① １つの席には１人しか座れない

\displaystyle \sum_{i \in I} x_{ij} = 1 \ (\forall j)

制約② １人につき１つの席にしか座れない

\displaystyle \sum_{j \in S} x_{ij} = 1 \ (\forall i)

制約③ 席には座るか否か

x_{ij} \in \{ 0 ,1 \} \ (\forall i\in I, \forall j\in S )

まとめて書くと今回解く最適化問題は以下のようになります。

\begin{align}
Maximize \hspace{22pt}& \displaystyle \sum_{i \in I} {W_i}^t x_i\\
subject \ to \displaystyle \sum_{i \in I} x_{ij} &= 1 \ (\forall j)\\
\displaystyle \sum_{j \in S} x_{ij} &= 1 \ (\forall i)\\
x_{ij} &\in \{ 0 ,1 \} \ (\forall i, \forall j )
\end{align}

pulpによる実装

定式化が完了したのでpulpを用いて実装して行きます。

pulpの使い方については以下の記事が非常にまとめられています。
https://qiita.com/mzmttks/items/82ea3a51e4dbea8fbc17

seat_change.py

import pulp
import random
import numpy as np


def main():
    n = 10
    seat = n
    W = np.zeros([seat,n])

    #値を入れる
    for i in range(seat):
        for j in range(n):
            W[i,j] = random.random()

    # 各行を割合に変換
    sumbox = W.sum(axis=0, dtype='float') 
    W /= sumbox


    # 問題の宣言
    problem = pulp.LpProblem(name='change seat', sense=pulp.LpMaximize)

    # 変数の宣言
    x = {(i,j):pulp.LpVariable(name='x_{}_{}'.format(i, j), cat='Binary') for i in range(seat) for j in range(n)}

    # 目的関数
    problem += pulp.lpSum([W[i,j]*x[i,j] for i in range(seat) for j in range(n)])

    #一つの席には一人だけ
    for i in range(seat):
        problem.addConstraint((pulp.lpSum([x[i,j] for j in range(n)]) == 1),"seat_limitation_{}".format(i))

    #ユーザーは１つの席のみに入る
    for j in range(n):
        problem.addConstraint((pulp.lpSum([x[i,j] for i in range(seat)]) == 1),"user_gets_onlyoneseat_{}".format(j))

    status = problem.solve()
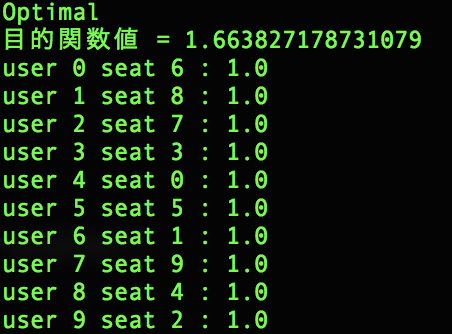
    print(pulp.LpStatus[status])
    print("目的関数値 = {}".format(pulp.value(problem.objective)))


    for j in range(n):
        for i in range(seat):
            if pulp.value(x[i,j]) > 0:
                print(f'user {j} seat {i} : {pulp.value(x[i,j])}')



if __name__ == '__main__':
    main()

③の制約は変数の宣言の際に'Binary'という形によって入っています。
また、生徒の希望度は今回、乱数を用いています。

実行すると以下のような結果が得られます。

このようにして席替え問題をpulpを用いて解くことができました。

最後に

整数計画法として解くことのいい面の１つとして、この基本の問題に対して制約を追加することでやりたい問題を解くことができることです。

例えば、
人に重み付けをして優先度を考慮する
隣り合う人の条件を加える
などが考えられます。どのように定式化するのかは考えてみてください。