巡回セールスマン問題
巡回セールスマン問題(以下TSP)についてご存知でしょうか。
完全グラフと全ての辺の移動コストが与えられた上で、全ての点を1回ずつ通り、始点に戻る巡回路の中で総移動コストが最小となる巡回路を求める組合せ最適化の問題です。
今回の記事の趣旨とは異なるため、ソルバーの詳細及びTSPを解くアルゴリズムの紹介は他の文献に譲ります。(個人的には辺の移動コストが定数でないTSP (dynamic TSP)にも興味があるので追ってまとめたいと思います。実応用としては、渋滞が発生して移動時間が変わる等の状況を考慮することに相当します。)
TSPの応用としてはその名についているように人が全ての与えられた場所の集合を回る、郵便物などの配送*やテーマパークで回る順番を考える問題が多いかと思いますが、それらの実空間で何かの対象物が移動する以外の面白いなと思った応用例について3つ紹介して行きたいと思います。
(* 実際の配送計画問題は時間指定やトラックの許容量など追加の制約が多く入るため、純粋にTSPとして定式化できるケースはまずないと思います。)
色集合から"自然な"カラーパレットの作成
Dynamic Closest Color Warping to Sort and Compare Palettes (SIGGRAPH'21)
著者スライド (本セクションの図はこちらから引用)
カラーパレットの中では複数の色が感覚的に自然な色の並びをしているかと思います。(少なくとも、赤・青・オレンジのような不自然な色の並びはないかと思います。)
例えばこういうものですね。
色達が与えられた元で自然な色の並びをしたカラーパレットを作成するという問題などをTSPに定式化して解いています。
色同士の類似度を測る方法としては、単にRGB値の差分の(二乗)和をとる、HSV表記をして差分を取る等考えられますが、本研究では色をCIELAB空間上の点として表した上でCIE DE2000を用いて類似度を定義しています。
参考: 色の距離(色差)の計算方法
Single Palette Sorting
まず、色集合が与えられた上でそれらを自然に並べたカラーパレットを作成したい問題を考えます。
上記の方法で色同士のコストを定義した上でTSPのsolverとしてはLKHを用いて解いています。
TSPの解は巡回路であるため、一列に並んでいるカラーパレットにするためにはどこかの枝を切る必要があります。その枝は、TSP解のパスに含まれる枝のコストの中で最大の枝を選んでいます。
個人的には後から枝を切るよりは、super source兼super sinkの仮想点を1つ作ってTSPを解いた方が良い解が求まると思います。(論文中で解いている問題は、カラーパレットの両端の色同士が"ある程度"似ていることを要請しているため。)
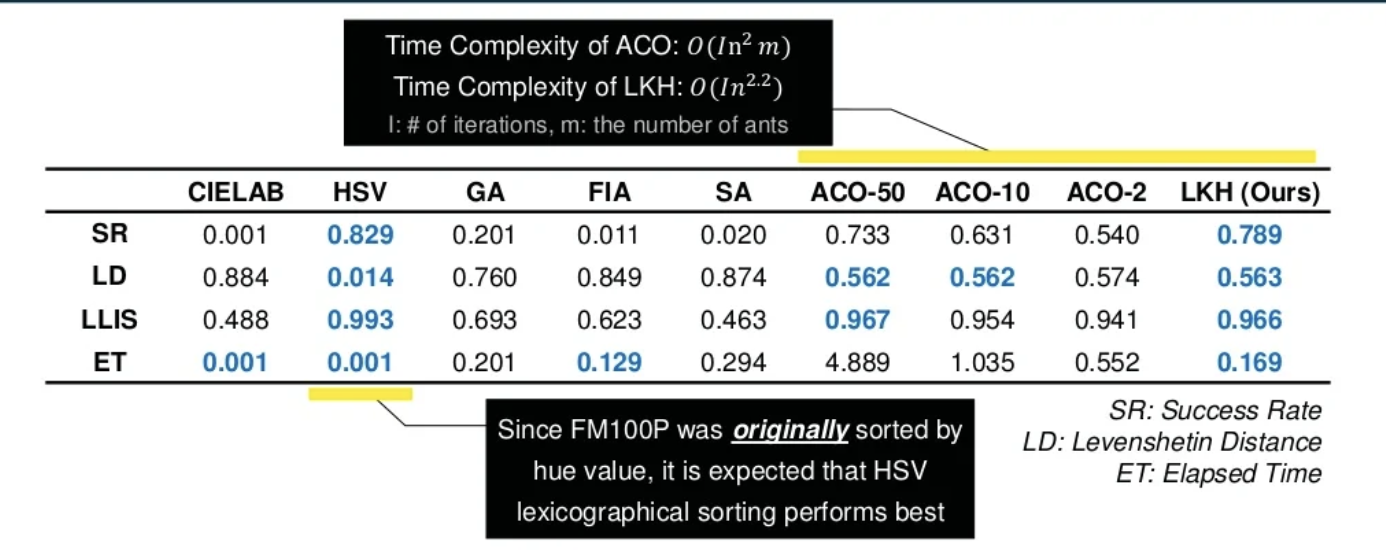
定量評価において、以下の3つの指標が利用されています。
ここでは説明の便宜上、提案手法で出力されたカラーパレットを予測パレット、正解データのカラーパレットを正解パレットと呼ぶことにします。
- Success Rate
- 正解パレットと予測パレットが完全に同じ割合
-
Levenstein Distance
- 正解パレットと予測パレットのLevenstein Distance (例えば、2つの文字列の類似度を計算する際に用いられる)
- Length of Longest Increasing Subsequence
- 予測パレットから順番を変えずに抜き出して作れる正解パレットの部分列の最長の長さ
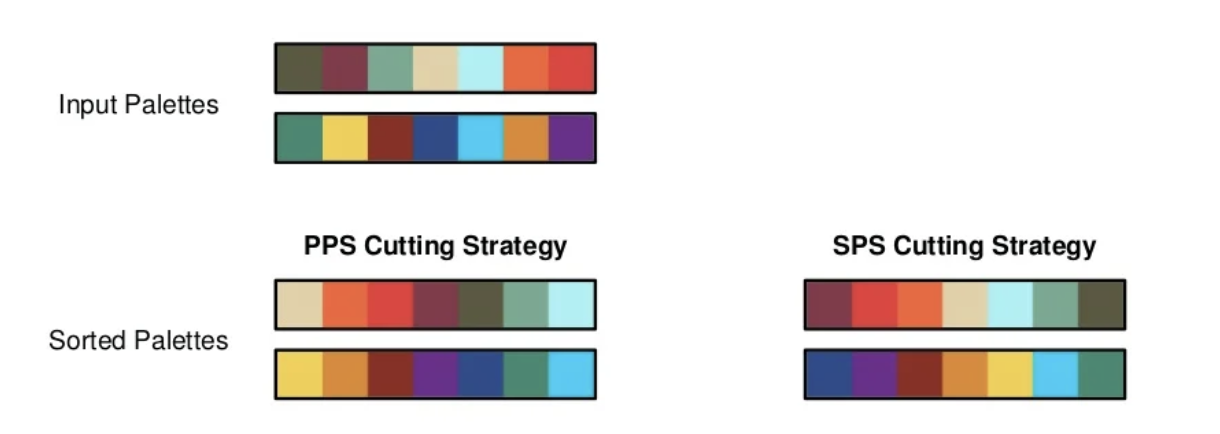
Palette Pair Sorting
次に、複数のカラーパレットを同時に並び替える問題について考えます。
この問題では、Single Palette Sortingで考えていた「色同士が”自然に”並んでいる」ことに加えて、「ソート後の2つのカラーパレットの各インデックスの色がある程度似ている」ことを実現しようとしています。
(一旦、与えられた色が2つのカラーパレットの色であることを忘れて、)Single Palette Sortingと同様に与えられた2つのカラパーレットに含まれる全ての色同士の類似度を計算し、LKH solverを用いてTSPを解きます。
「ソート後の2つのカラーパレットの各インデックスの色がある程度似ている」ためにどの枝を切るのかを考える必要があります。
手順
- TSPを解いた結果同一カラーパレット内の最長の2つの色のペア(点のペア)を考える。(TSPを解いた結果、それぞれのカラーパレット同士が一般に交互に並んでいるとは限らないことにも注意)
- 2つの点を結ぶTSPの解のパスのうち、点数が少ない方を抽出 (TSPの解は巡回路なので2パターンパスが存在する)
- そのパスの中で最も枝のコストが大きい枝を選択する
それぞれのカラーパレットに対してSingle Palette Sortingを解いた結果との比較が載せられています。(下図参照: PPS : Pair Palette Sorting, SPS : Single Palette Sorting)
例では、2つのカラーパレットかつ長さが同じパレットの並び替えの結果が載せられていますが、この手法自体は3つ以上のカラーパレットを同時に並び替える場合やカラーパレット同士の長さが異なる場合にも適応可能です。
Similarity Measurement
他にも、与えられた2つのカラーパレットの類似度をどのように求めるのか?という問題についても手法が提案されています。
既存手法は、2つのカラーパレットの要素毎(element-wised)に何かしらの類似度を計算しているとのことですが、カラーパレットの全体(flow-based)の類似度を測る指標を提案しています。
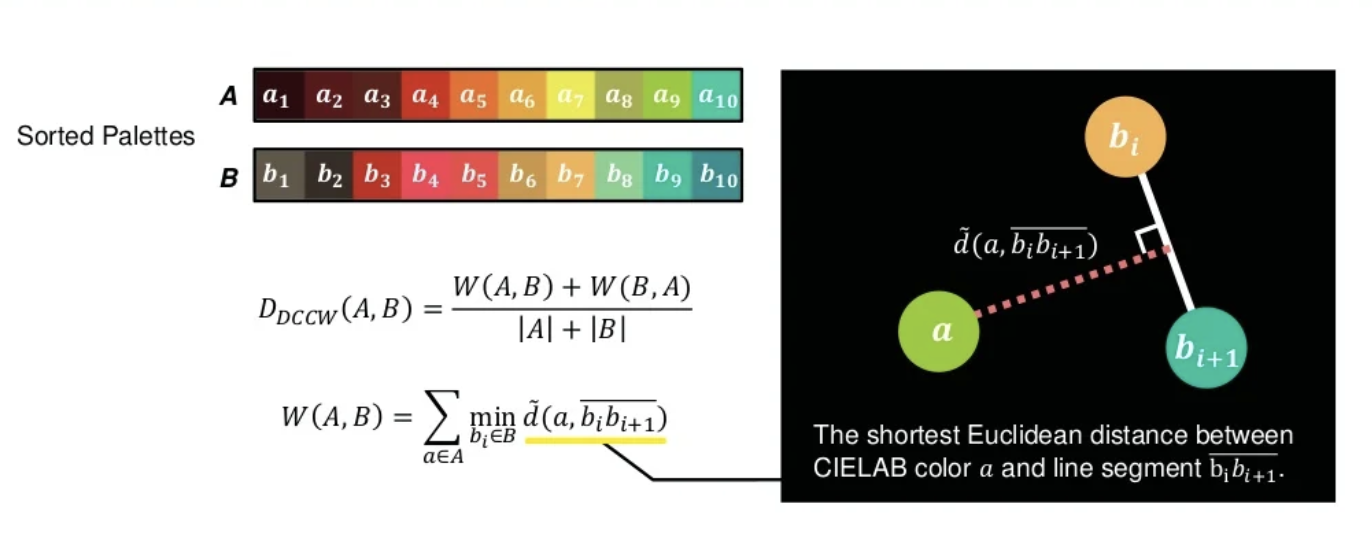
その手法を Dynamic Closest Color Warping (DCCW) と名付けています。
2つの時系列データの類似度を測る方法としてDynamic Time Warping (DTW) をご存知の方は、それを思い浮かべながら読んで頂けると理解が早いかと思います。
DTWでは与えられた2つの系列データの中の適当な2つの要素同士の距離の和を用いて計算されますが、DCCWでは、ある系列データの1つの要素から、もう1つの系列データの隣り合う2つのデータのペアに下ろした垂線の長さを用いてDCCWで用いる $W(A,B)$ が定義されています。(この辺りがflow-basedと主張している所以かと、下図参照)
本研究の応用例としては、下記が挙げられています。
-
Palette Interpolation
- 文字通り色の補完
-
Palette Navigation
- 類似パレットの抽出により雰囲気の似た写真/デザイン物の抽出
-
Image Recoloring
- 与えられたパレットの色に基づいて画像の色彩変更(上記Palette Pair Sortingを使って可能)
単語の埋め込み
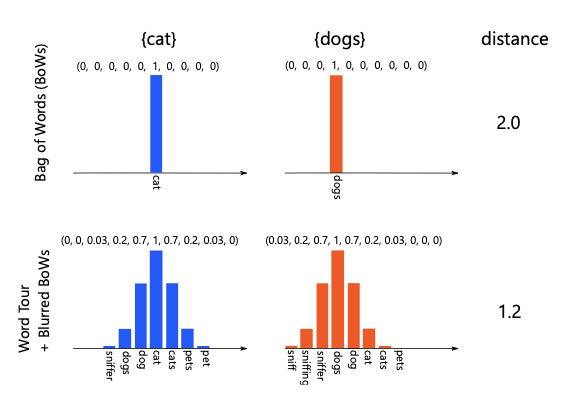
Word Tour: One-dimensional Word Embeddings via the Traveling Salesman Problem (NAACL 2022)
(図は上記論文またはスライドより引用)
次の対象は単語の埋め込みです。
Wordをなんと1次元ユークリッド空間に埋め込んでしまおうという研究です。(Poincare Embeddingでは5次元双曲空間へ埋め込み)
単語埋め込みが満たしていて欲しい性質を以下の2つとして提案しています。(自然な議論だと思います。)
- 健全性: 近くに埋め込まれた単語であれば意味は近い
- 完全性: 意味の近い単語であれば近くに埋め込まれる
1次元に埋め込むということで、完全性を諦めて健全性を満たすように埋め込みを考えます。
つまり、一次元埋め込みで隣り合う単語は元の埋め込み上で近いようにTSPとして定式化をします。
各単語に対して高次元の単語のベクトル表現(今回はGloVe)が与えられている前提で、移動コストとしては、そのベクトル同士の距離を用います。
ソルバーとしてはKLHを用いていました。
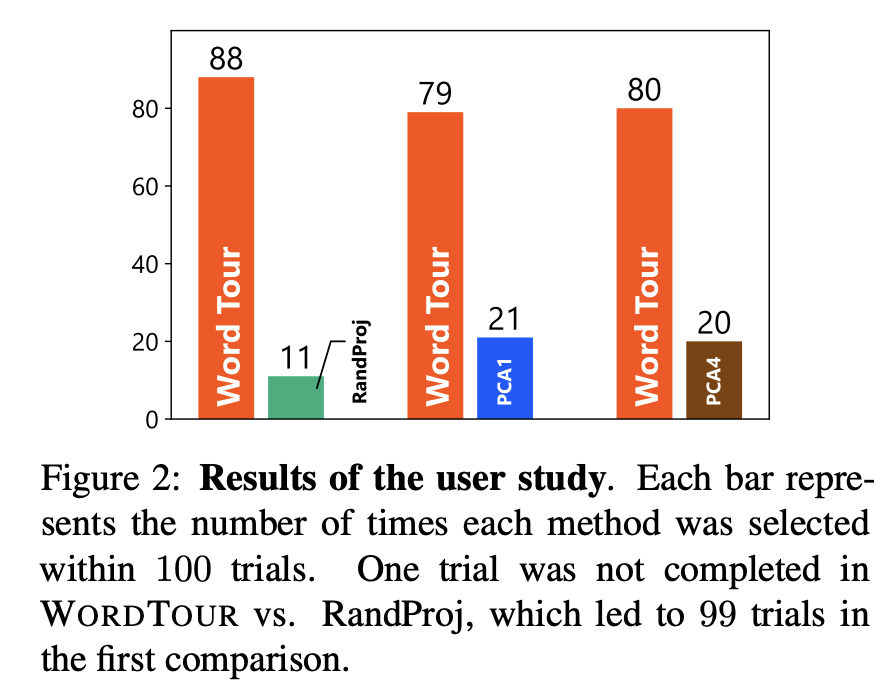
定性的な評価として、得られた1次元埋め込みの中で特定の単語の近くにある単語が意味の近い単語か(健全性)をみています。
定量評価の1つとして、ある単語を抽出し、埋め込まれた空間上で最も近い単語を抽出することを各手法ごとに行い、どのペアが類似しているかをアンケートベースで評価しています。
また、文書同士の類似度の評価にWordTourで得られた埋め込みを用いることについても言及されています。
文書内の与えられた単語及び埋め込んだ先で近い単語を獲得し、文書内の単語を中心とした正規分布を考え、その重ね合わせで文書の特徴ベクトルを表現し、$L_1$距離やword mover's distanceを用いて類似度を測っています。
単純にbag-of-wordsで測る場合では取れない表記揺れ等も吸収できていると思います。
これは、リアルタイム処理が求められるようなケースについてはかなり有難いと思います。
ちなみにこの論文の著者の方が青本シリーズの最適輸送を鋭意執筆中とのことです。
音楽のプレイリスト作成 (Spotify)
最後は論文として発表されている訳ではなさそうですが(僕が見逃していたら教えてくださいorz)、事例として紹介します。
spotifyにおいて曲達が与えられた元でプレイリストを作成する問題をTSPとして定式化して解いています。
コストとしてはムードやBPM等の差分の重み付き和で定義されているようです。(詳細な記述なし)
解くアルゴリズムとしてはシンプルなNearest Neighbor法(現在の点から未走査の点の中で最も近い点に移動することを未走査の点が無くなるまでgreedyに繰り返す)が使われています。(初期点はランダム)
ツールも公開されているのでSpotifyアカウントのある方はぜひ遊んでみてください。
ちなみに、APIなどのシステムへの組み込みに興味のある方はこちらのリンクの内容もおすすめです。
読んで頂きありがとうございました。
TSPと名前だけ聞くと人が実際に移動することを思い浮かべがちかと思いますが、ペアに対してコストが定義されている集合を”自然に”並び替える問題だと思うとこのような応用例が考えられるのだなと思いました。
誤解があれば指摘頂けると助かります。
また、感想や他にも面白い研究についてご存知でしたらコメント頂けると嬉しいです。