はじめに
最近Unityをはじめました。前からCADさわったりはしていたので，3次元の概念については余裕だろ〜と思っていました。
なんですかQuaternionって。
パラメータが4つってどういうことですか。
リファレンスを読んでも
クォータ二オンは複素数に基づいており、直感的に理解するのは容易ではありません。個々のクォータニオンの成分 (x,y,z,w) にアクセスしたり変更したりすることはほとんどありません。たいてい、既存の回転 (例えば、Transform から取得) を使用して新しい回転を構築するために使用します (例えば、2 つのローテーションの間を円滑に補間するなど)。使用する Quaternion 関数の 99% は、Quaternion.LookRotation、Quaternion.Angle、Quaternion.Euler、Quaternion.Slerp、Quaternion.FromToRotation、Quaternion.identity です (他の関数が使用されることはほとんどありません)。
とあり，「サジ投げとるやないかい！」と思ったのでめっちゃ頑張って勉強しました。
間違っていたらあたたかく指摘していただけると嬉しいです
(ちなみに私は一応理系なので語彙があれな時はまあそういうことです)
参考
本記事はを書くにあたって以下の記事で勉強しました。
ありがとうございます
超ざっくり複素数平面
詳しい人に怒られそうな感じでやっていきたいと思います！(高校数学だしいけると思うので)
わかる方はこの項目飛ばして大丈夫です。
平面上の任意の点を表現するとき，以下のような座標の表現をします。
P(x座標, y座標)
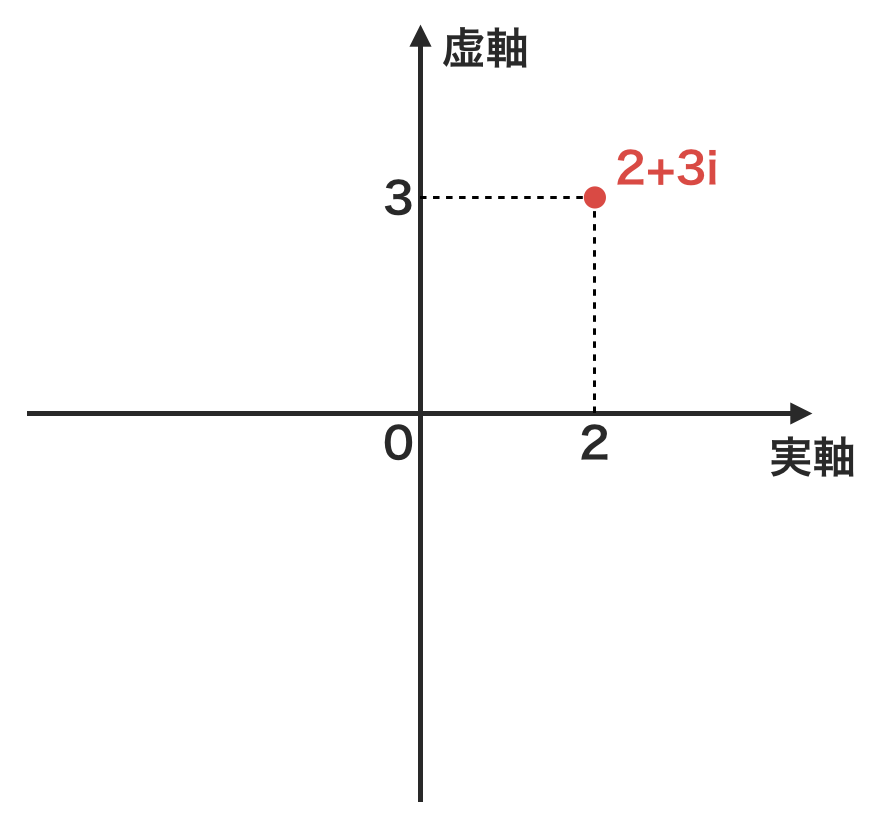
複素数平面では，この時のx軸を**実軸**，y軸を**虚軸**として以下のような表現をします。
P(実軸の座標, 虚軸の座標 i)\\
(iは虚数単位)
この虚数平面上に，半径1の円があると考えます(**単位円**)。
この円周上にある点は以下の複素数で表現することができます。
\cos\theta+i\sin\theta\\
(iは虚数単位)
ここで，実部が0の複素数`i`が表現する点を考えます。`i`は`θ=90°`の位置の点を表現しています。
この`i`にさらに`i`をかけると
i\times i = -1
となります。このとき，-1が表現する点を考えると単位円上のθ=180°の点になります。
さらにiをかけると-iとなり，この点が表現する点は単位円上のθ=270°の点です。
図に示すとこんな感じ。
つまり，単位円上の点を掛け合わせること＝回転角を足すことになります。
平面から立体へ
アイルランドの数学者ウィリアム・ローワン・ハミルトンは(たぶん)考えました。これを三次元空間の力学に応用できないか。
これによって生まれたのがQuaternionです。
虚数で3次元空間を表現するために，ハミルトンは虚数単位を3つ作って解決しました。(本記事ではi，j，kとします)
この虚数単位は以下のようなものであると定義されました。
i^2=-1, j^2=-1, k^2=-1\\
ij=k, ji=-k\\
jk=i, kj=-i\\
ki=j, ik= -j\\
ijk=-1
虚数単位が3つにふえた複素数は以下のような数として表現できます。
ix+jy+kz+w\\
(x,y,z,wは実数)
そしてこれは(x,y,z)の向きにw進んだ位置(ベクトルの大きさ)の点を示します。
これらの係数をまとめたものをQuaternionとしました。
(つまりQuaternionは本来回転を示すものではないです)
Quaternion=(x, y, z, w)
これに以下の条件を付与することで回転に限定して考えられるようになります。
x^2+y^2+z^2+w^2=1
回転したい！
先ほど，単位円上の点を掛け合わせること＝回転角を足すことという話をしました。
つまりQuaternionをいい感じにかけたら回転ができるのではないか…
では以下の点PをV分だけ回転させた点P'を考えていきます。実部はベクトルの大きさを示すパラメータなので，Vの実部は0です。
ここで，実部の係数が0のQuaternionをpure quaternionと呼びます。
P=p_1i+p_2j+p_3k+p_4\\
V=v_1i+v_2j+v_3k+0
ではいざかけてみましょう！
となりましたが純粋にPとVをかけても回転後のPの角度は求められません…
なぜなら実部が残ってしまうから。これを消すために，以下のように計算すると，wが0になって，計算結果がpure quaternionになります。
P'=PVP
こうするとうまく回転します。
おわりません
虚数単位が3つある複素数は以下のように表現できるという話でした。
ix+jy+kz+w\\
(ｘ, y, z, wは実数)
しかし，虚数単位が1つだった時cosθ+isinθと表現したように，θを使おうとしたときに問題が発生します。
Pを2回かけているので最初の位置がθではなく2θになっています…
ということでθを2分の1して，以下のような表現になります。
\cos\frac{\theta}{2}+(ix+jy+kz)\sin\frac{\theta}{2}
完全に理解した…
結論
Quaternion.Angle，Quaternion.Eulerを使おう。
UnityのrotationをQuaternionで直接いじりたくて勉強しましたが，私には無理だということがわかりました…
大人しくQuaternion.Angleでオイラー角に直してからQuaternion.EulerでQuaternionに戻します…
ありがとうございました