水文水質DBのデータを使って確率水文統計

確率水文統計

百年に一度の雨量，洪水などよく耳にする言葉ですが，それはどのように計算されているのでしょうか？我々の持っている観測データは通常，数十年間の期間に限られています．したがって，今ある観測データがどのような確率分布に従っているかを調べ，そこから極値を推定することになります．

ここでは，水文水質データベースからデータを持ってきて，年最大流量に対して確率水文統計を行う簡単な方法について述べます．

※筆者の水文統計に関する知識は，大学の講義で習った程度であることを踏まえて参照いただければ幸いです．詳細については，別途専門書等を参考ください．

データの取得

水文水質データベースには様々な観測値が集約されています．

検索方法はいろいろありますが，地図からの選択がやりやすいでしょう．

ここでは，北海道の忠別川，暁橋(旧)（廃止）を見てみましょう．

※場所を選択する操作性はいまいちですね．．

観測地点をクリックすると，利用可能なデータが出てきます．

色々とデータはありますが，ここでは年最大流量の解析を行いたいので，「流況表検索」を選択します．

左上でデータを取得したい期間が出てくるので，利用可能な範囲すべてを選択します．そうすると，最大流量，最小流量などいろいろな水文量が年度ごとにまとめられた表が出てきます．

ここでは年最大流量を解析するので，左から２列目のデータを使います．エクセル等にコピーして，この行だけテキストファイルで保存します．（エクセルに保存してPandasを直接使えば簡単かな．．）

テキストエディタは，Visual Studio Codeが使いやいですね．

ようやくTeraPadから脱却．．

対数確率紙へのプロット

年最大流量など，大きい流量がたまにしか生じない値は，発生確率が小さい流量のほうによった分布をすることが知られています．そのような分布として簡単なものに対数正規分布があります．つまり，流量の対数を取ったとき，確率密度分布が正規分布になるような分布です．

先ほど取得したデータをPython + Matplotlibを使って対数確率紙へプロットしてみましょう．使っている環境は，Anaconda 3のSpyderになります．

Python + Matplotlibの利用は下記のサイトを参考にしています．

プロッティングポジションとしては，カナン公式を使っています．

# Include some libraries 

import matplotlib.pyplot as plt
import numpy as np
from scipy.stats import norm # normal distribution
from scipy import optimize
from statistics import mean, median, variance, stdev

def func(parameter,x,y):
    a = parameter[0]
    b = parameter[1]
    residual = y-(a*x+b)
    return residual

def gumbel(ff):
    pp = -np.log(-np.log(ff))
    
    return pp;

def plotposition(rr):
    rs = sorted(rr,reverse=True)
    nn = len(rs)+1
    pf = list(range(1,nn))
    
    pp = []
    ff = []
    
    for i in pf:
#        wp = (2*float(i)-1)/float(2*nn)     # Hazen plot
        wp = (float(i)-0.4)/float(nn+1-0.8)  # Cunnane plot
        wf = 1-wp
        pp.append(wp)
        ff.append(wf)
    
    ppp = norm.ppf( ff, loc=0, scale=1 )
#    ppp = gumbel( ff )
    qqq = np.log10(rs)
    
    parameter0 = [0.0,0.0]
    result = optimize.leastsq(func,parameter0,args=(ppp,qqq))
    aa=result[0][0]
    bb=result[0][1]
    
    return ppp,qqq,aa,bb


# open input file


with open("obs-before.txt","r") as fpin:
    lines = fpin.readlines()
    rro = []
    for line in lines:
        value = line.replace('\n', '').split('\t')
        rro.append(float(value[0]))
    
fpin.close()


# ploting position 

po, qo, ao, bo = plotposition(rro)

print(ao, bo)

pdef = 0.99

p_def = norm.ppf(pdef)
logq_pdef = ao*p_def+bo

# plot the data on the log-normal probability paper

plt.figure(figsize=(5,9))

xmin=np.log10(10)
xmax=np.log10(1000)
ymin=norm.ppf(0.001, loc=0, scale=1)
ymax=norm.ppf(0.999, loc=0, scale=1)
#ymin=gumbel(0.001)
#ymax=gumbel(0.999)
plt.xlim([xmin,xmax])
plt.ylim([ymin,ymax])
plt.tick_params(labelbottom=False)
plt.tick_params(labelleft=False)
plt.tick_params(which='both', width=0)

plt.plot(qo,po,'o',color='k',markersize=2)

plt.plot([xmin, xmax], [(xmin-bo)/ao, (xmax-bo)/ao], color='k', linestyle='-', linewidth=1)

plt.plot([xmin, logq_pdef], [p_def, p_def], color='r', linestyle='-',linewidth=2)

plt.plot([logq_pdef, logq_pdef], [ymin, p_def], color='r', linestyle='-',linewidth=2)



# setting of x-y axes
_dy=np.array([0.001,0.01,0.1,0.5,0.9,0.99,0.999])
dy=norm.ppf(_dy, loc=0, scale=1)
#dy=gumbel(_dy)
plt.hlines(dy, xmin, xmax, color='grey',linewidth=0.5)
#_dx=np.array([1,10,100])
_dx=np.array([10,20,30,40,50,60,70,80,90,100,200,300,400,500,600,700,800,900,1000])
dx=np.log10(_dx)
plt.vlines(dx, ymin, ymax, color='grey',linewidth=0.5)

fs=10
for i in range(1,4):
    plt.text(float(i), ymin-0.1, str(10**i), ha = 'center', va = 'top', fontsize=fs)

for i in range(0,6):
    plt.text(xmin-0.01, dy[i], str(_dy[i]), ha = 'right', va = 'center', fontsize=fs)
    
plt.text(0.5*(xmin+xmax), ymin-0.5, 'Discharge (m$^3$/s)', ha = 'center', va = 'center', fontsize=fs)
plt.text(xmin-0.25,0.5*(ymin+ymax),'Non-exceedance probability', ha = 'center', va = 'center', fontsize=fs, rotation=90)


ss = "Q={0:.0f} m$^3$/s".format(10**logq_pdef)

plt.text(logq_pdef*0.95, dy[1], ss, rotation=90)

plt.savefig("SemiLog_Qmax.jpg",dpi=300)
plt.close()

#で消している部分にするとGumbel分布になるはずです．

obs-before.txtが水文水質データベースから取得した年最大流量になります．

これを動かすと以下のような図を取得できます．黒い点が観測値でそれを最小二乗法で近似したものが直線となっています．ばらつきはあるもののそれなりに直線，つまり対数正規分布に従うことが見て取れます．（本当は何かしらの検定が必要かな．．）

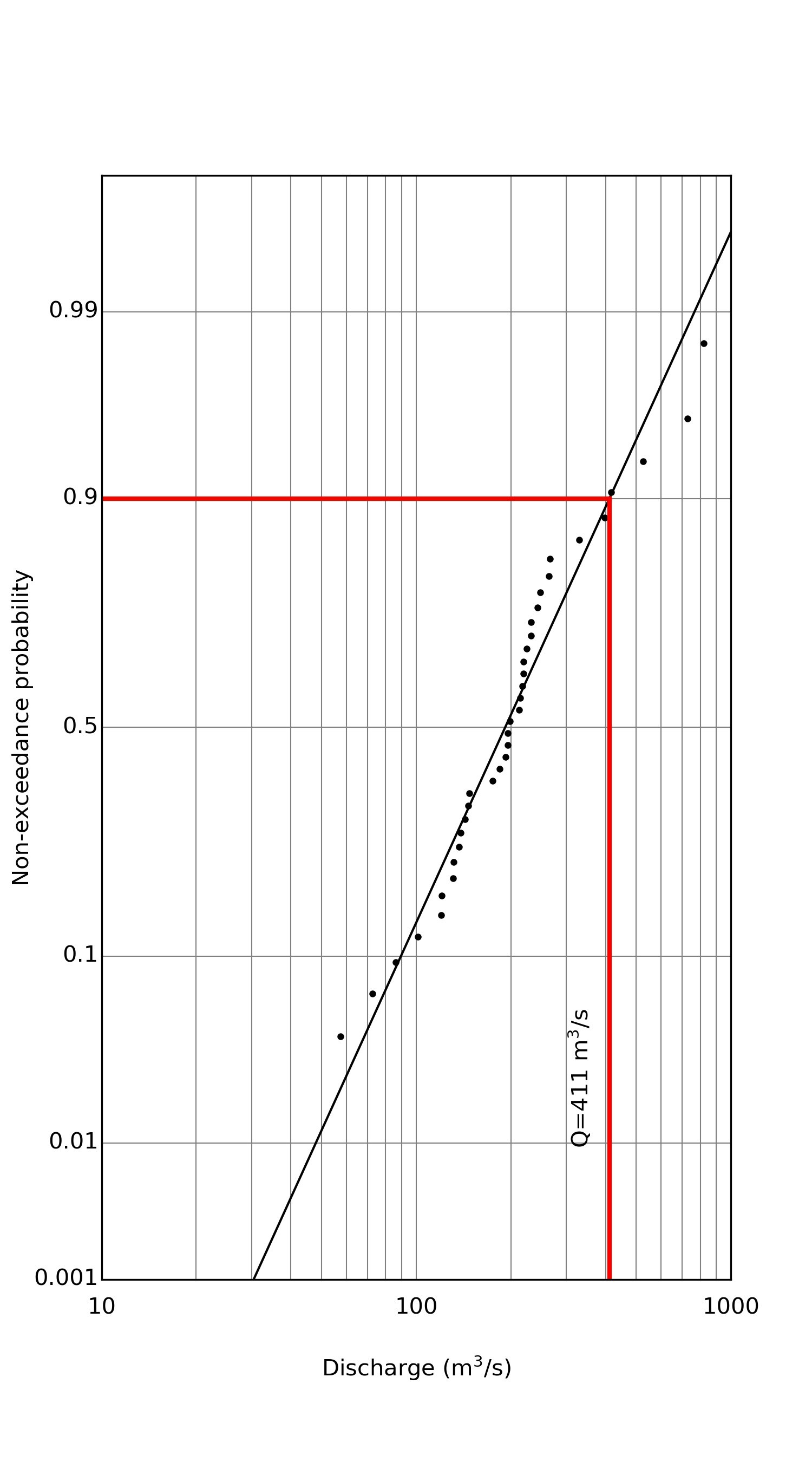
この図から，再現期間10年，つまり10年に一度の確率で発生する流量を推定してみましょう．

再現期間が10年ということは生起確率が10%ですから，図の縦軸の非超過確率に直すと90%のところを見ればよいことになります．

グラフの赤線のようにたどると非超過確率90%流量（=再現期間10年)の流量は411m$^3$/sという結果となりました．

ダムによる流量カットの影響

忠別川では，2006年に忠別ダムの運用が開始されています．これが下流の流量にどのように影響するかを見てみましょう．

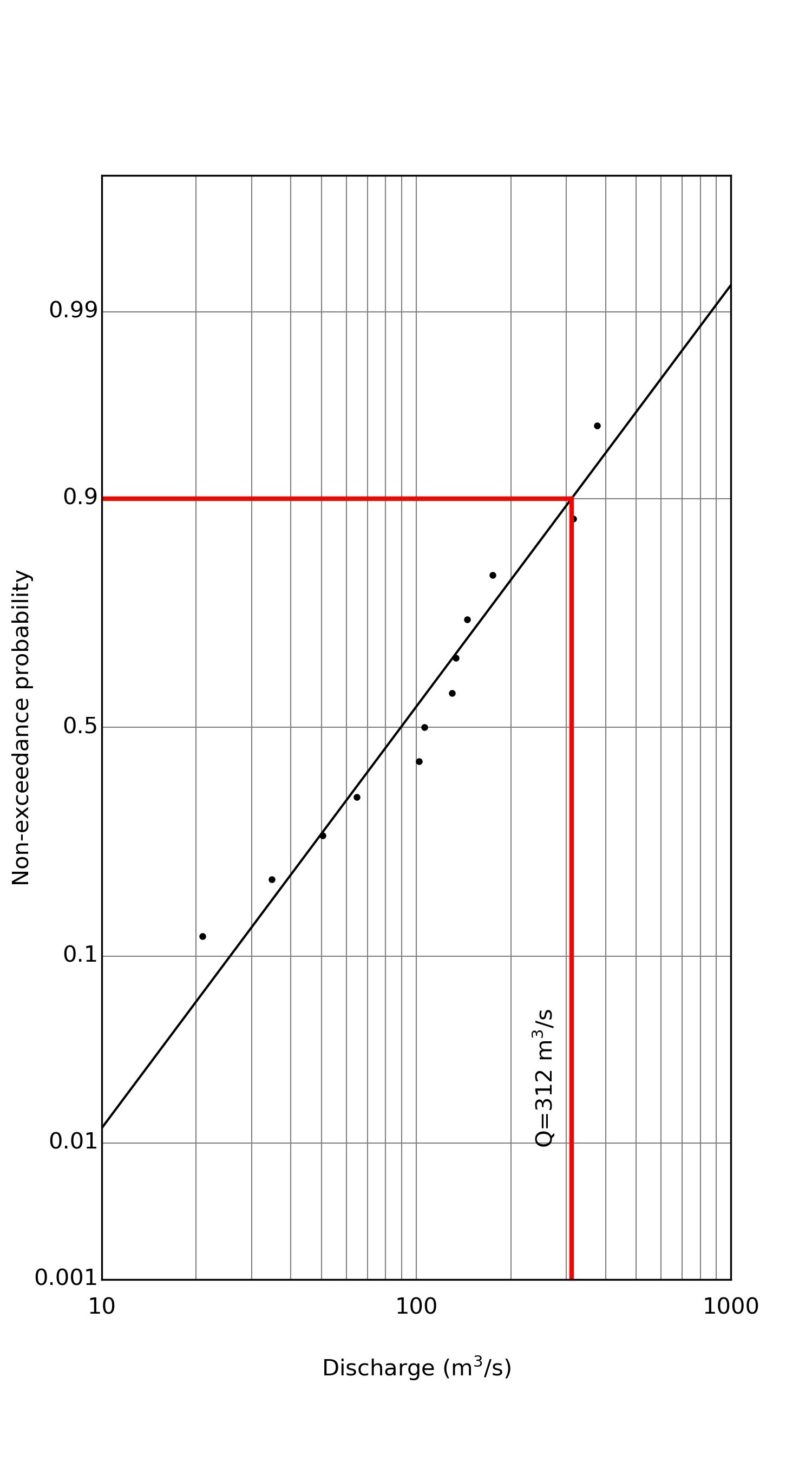
先ほどの水文水資源データベースに戻り，暁橋(旧)（廃止）の右にある暁橋という観測点から同様のデータを抽出して，同じ解析をしてみましょう．

そうすると今度は，10年確率流量が312m$^3$/sに下がりました．データは少ないですが，ダムによってピーク流量がカットされている影響がうかがえます．

追記：水文水資源データベースではなく，水文水質データベースですね．．大変失礼しました．