交互砂州の波長と波高を算出してみる
前回の記事で,iRICから出力したcsvファイルを使って可視化などをしてみましたが,今回は直線水路の交互砂州計算において砂州の波長と波高を算出し,可視化してみます.
あまり用途はないと思いますが,計算結果をいじる一例として残しておきたいと思います.
Nays2DHによる交互砂州の計算
ここでは,渡邊・桑村による砂州実験におけるS50を対象とする.詳細は論文を参照いただくとして,実験諸量は以下になります.
水路長: 約40m
水路幅: 0.9mで一定
勾配: 0.0125
粒径: 中央粒径0.76mm(東北珪砂4号)
流量: 10.35l/s (定常)
これをiRIC-Nays2DHにより再現計算してみます.上記実験条件に沿って計算条件を設定しますが,重要な点のみ下記にまとめます.
・水路長は40mとして周期境界条件.
・砂州形成のきっかけとして,上流端より若干下流の右岸付近の河床高さを0.001m上げる
・マニング粗度は粒径見合いで0.0145と一定値
・二次流強度はゼロ(つまり二次流は考慮しない)
・計算格子数は流下方向400,横断方向15
・計算時間刻み0.01秒
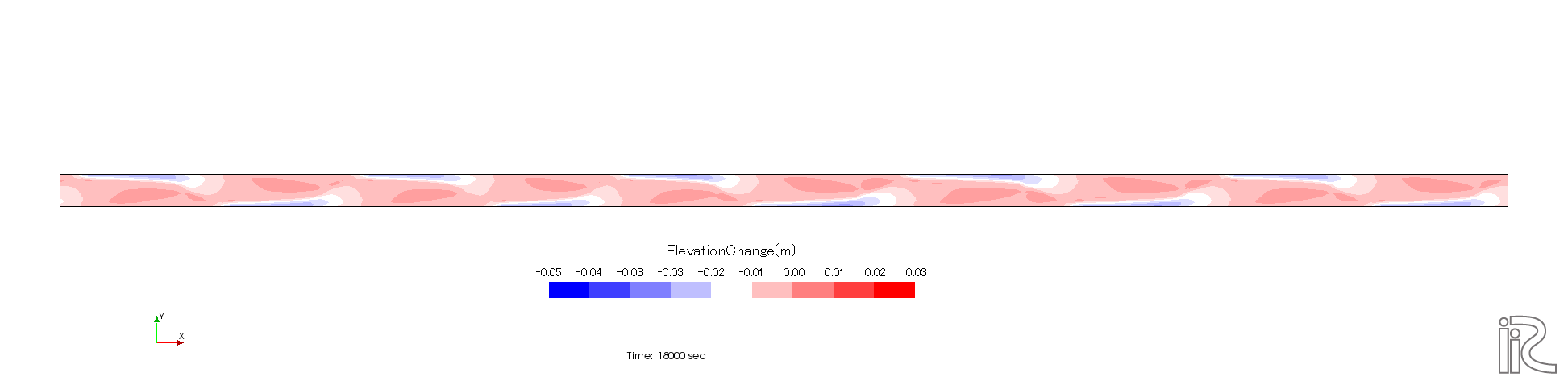
この結果,以下のような交互砂州が計算できました.とても明瞭な交互砂州が形成されています.
計算結果のMatplotlibによる可視化と交互砂州波長・波高の算出
まず,前回の記事でも示したように計算結果をcsvファイルとして出力しておきます.これを読み込んで波長と波高を算出してみましょう.
砂州波長は砂州1単位(1つの交互砂州という意味)の長さになりますが,波高の定義は2つあり,砂州1単位における1)同一断面内の最大・最小河床高の差の最大値,2)単純な最大と最小の河床高さの差です.
ここでは後者を求めてみますが,多少の変更で前者にも対応できるはずです.
まずは砂州1単位を抽出する必要がありますが,ここでは側壁付近の河床変動高さについてゼロアップクロス法を適用して1単位を特定します.そしてこの1単位中の最大・最低河床変動量の差を波高を求め,計算領域内で平均を取ることで波長・波高を求めます.
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import numpy as np
import csv
import os
import re
import shutil
# 砂州の波長,波高を変える関数
def length_height(x,y,z):
s = x[0,:] # 側岸沿いの距離
wdz = z[0,:] # 側岸沿いの河床変動量
dz = wdz-np.mean(wdz) # 平均的な河床変動量を差し引いておく
# 横断面内での最大の侵食・堆積量を算出
zmin = []
zmax = []
nx = len(s)-1
for i in range(nx+1):
zmin.append(min(z[:,i]))
zmax.append(max(z[:,i]))
# ゼロアップクロス法で交互砂州1単位を抽出
ip = []
for i in range(nx):
if np.sign(dz[i])<0. and np.sign(dz[i+1])>0. and np.abs(zmax[i]-zmin[i])>0.001:
ip.append(i)
nn = len(ip)-1
ll = []
hh = []
# 砂州1単位における波長と波高(1単位中の最大高さと最小高さの差)を計算
for n in range(0,nn-1):
wl = s[ip[n+1]]-s[ip[n]]
wh = np.max(zmax[ip[n]:ip[n+1]])-np.min(zmin[ip[n]:ip[n+1]])
# 有効とする範囲を決めたければ制限を付ける
if s[ip[n]]>5. and s[ip[n]]<35.:
ll.append(wl)
hh.append(wh)
# 上記算出値の平均値を波長と波高とする
L = 0.
H = 0.
nb = len(ll)
if nb>=1:
L = np.mean(ll)
H = np.mean(hh)
return L, H
この関数を使うことで各時刻における砂州波長と波高を求めてみましょう.
まず,読み込みフォルダなどの設定を行います.この辺は,前回の記事と同じです.
path_list = 'D:/HLL/original/watanabeS-50/bous/'
wip = os.listdir(path_list+"csv/")
wwip = []
for ip in wip:
mmm = re.search("[0-9]+", ip)
www = (mmm.group(), ip)
wwip.append(www)
aaa = sorted(wwip, key=lambda wwip: int(wwip[0]))
inputfiles = []
for aa in aaa:
inputfiles.append(aa[1])
fig_path = path_list+"/fig/"
if os.path.exists(fig_path):
shutil.rmtree(fig_path)
os.mkdir(fig_path)
次に,連番のcsvファイルから河床変動量を取ってきて,これを上記関数に渡すことで砂州波長と波高を求めていき,その結果をtb, lb, hbにそれぞれ保存しておきます.
計算結果を読むついでに河床変動コンターも作成しておきます.
tb = []
lb = []
hb = []
for inputfile in inputfiles[::5]:
filename = os.path.splitext(os.path.basename(inputfile))[0]
foldername = os.path.dirname(inputfile)
figname = fig_path+filename+".jpg"
with open(path_list+"csv/"+inputfile, 'r') as ifile:
data = csv.reader(ifile, delimiter=",")
header = str(next(data))
number = next(data)
index = next(data)
wwt = header.replace('\n', '').split()
wt = str(wwt[-1])
tt = float(wt[0:-2])
nx = int(number[0])-1
ny = int(number[1])-1
x = []
y = []
z = []
for row in data:
x.append(float(row[2]))
y.append(float(row[3]))
z.append(float(row[7]))
wX = [[0 for i in range(nx+1)] for j in range(ny+1)]
wY = [[0 for i in range(nx+1)] for j in range(ny+1)]
wZ = [[0 for i in range(nx+1)] for j in range(ny+1)]
X = np.array(wX, dtype="f8")
Y = np.array(wY, dtype="f8")
Z = np.array(wZ, dtype="f8")
y_offset = 0.45
ij = 0
for j in range(ny+1):
for i in range(nx+1):
X[j][i] = x[ij]
Y[j][i] = y[ij]
Z[j][i] = z[ij]
ij = ij+1
L, H = length_height(X,Y,Z)
tb.append(tt)
lb.append(L)
hb.append(H)
print(tt/60,L,H)
plt.figure(figsize=(10,2.5),tight_layout=True)
plt.axes().set_aspect('equal')
plt.xlabel('X(m)')
plt.ylabel('Y(m)')
plt.subplots_adjust(bottom=0.2)
zmin = -0.05
zmax = 0.025
xmax = 35.
xmin = 20.
ymin = -y_offset
ymax = y_offset
plt.axis([xmin,xmax,ymin,ymax])
plt.xticks( np.arange(xmin,xmax*1.01,5) )
plt.yticks( np.arange(ymin,ymax*1.01,y_offset) )
levels = np.linspace(zmin,zmax,51)
labels = np.linspace(zmin,zmax,6)
plt.title("Time= {0:.0f} min".format(tt/60))
plt.contourf(X, Y, Z, levels, cmap=cm.copper, extend="both")
plt.colorbar(ticks=labels, label='Bed evolution (m)', orientation='horizontal', fraction=0.09, pad=0.3)
plt.savefig(figname, dpi=600)
plt.close()
ifile.close()
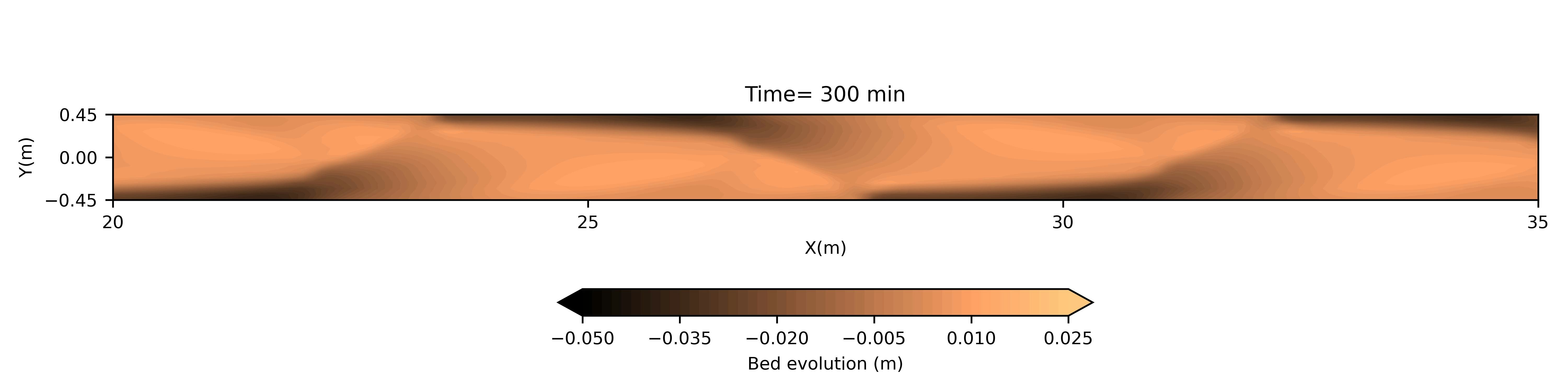
以下のような河床変動コンター図の連番が得られます.
得られた砂州の波長・波高の時間変化を可視化してみます.matplotlibのsubgridをつかって2つの図をまとめて書いてみました.
tmax = 300.
time = np.array(tb,dtype="f8")/60.
length = np.array(lb,dtype="f8")
height = np.array(hb,dtype="f8")*100.
plt.figure(figsize=(4,3),tight_layout=True)
plt.subplots_adjust(wspace=0.4,hspace=0.4)
plt.rcParams["font.size"] = 8
ax1 = plt.subplot2grid((2,1),(0,0),colspan=1)
ax2 = plt.subplot2grid((2,1),(1,0),colspan=1)
ax1.set_xlim([0,tmax])
ax1.set_ylim([0,10.])
ax1.set_ylabel('Wavelength (m)')
ax1.tick_params(labelbottom=False)
ax2.set_xlim([0,tmax])
ax2.set_ylim([0,7.5])
ax2.set_xlabel('Time (min)')
ax2.set_ylabel('Waveheight (cm)')
ax1.plot(time,length,'-',color='k')
ax2.plot(time,height,'-',color='k')
plt.savefig(path_list+'wavelengthheight.jpg', dpi=300)
plt.show()
plt.close()
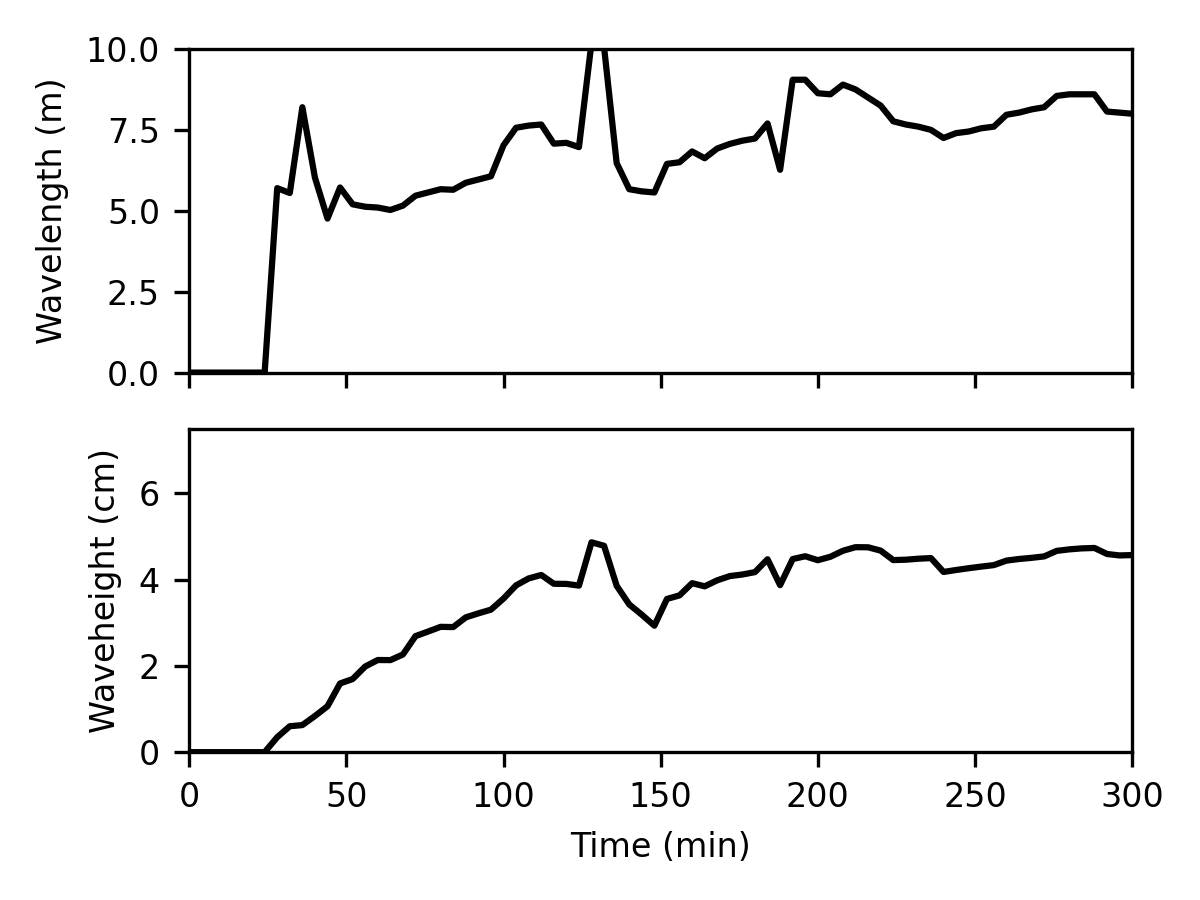
以下のような図が得られます.
徐々に波長と波高を増加させながら平衡状態に至る過程がわかります.実験結果によると平衡状態の砂州波長と波高がだいたい6m,5.5cmなのでまずます良い結果が得られているのではないでしょうか.
途中,波長や波高が時間的に大きく変動しているところは,計算における砂州の動態が不安定だったこともありますが,砂州1単位の抽出がうまくいっていないのかもしれません.砂州以下の細かな変動があってそれを拾ってしまった可能性もあります.必要に応じて改良が必要そうです.