RSA鍵の要素と暗号化

普段何気なく使っている（？）RSA鍵と暗号化アルゴリズムについての覚書。
なお、数学的な素養は皆無に等しいため、難しいこと（数式の解説）はナシ。中ではこういう計算をしているんだなという程度。

RSAの公開鍵と秘密鍵が具体的にどういう要素からなり、どうやって作られ、どのように暗号・複合に使われるのかをまとめる。

鍵生成のステップ（オリジナル）

1. 大きな（いわゆる鍵長の1/2程度のビット数で）素数を2つ生成する（$p$と$q$とする）
2. 以下を算出する
   • $n = p \times q$
   • $\phi = (p -1) \times (q - 1)$
3. 公開指数$e$を決定する（$1 < e < \phi$であり、$\phi$との最大公約数が1である数、つまり互いに素である）
4. 秘密指数$d$を決定する（$1 < d < \phi$であり、$e \times d \equiv 1 (mod \quad \phi)$を満たす、つまり$(e \times d) \div \phi$の余りが$1$）

つまり、最初の$p$と$q$を決めれば、あとは導出できるということになる。こうして決められた$n$と$e$が公開鍵であり、$d$、$p$、$q$が秘密鍵（知られてはいけない情報）ということになる。

ここで出てきた数値の意味は以下のようになる。

数値	呼名	使い道
$n$	modulus（法）	暗号・複合の両方で使用する
$e$	public exponent（公開指数）	暗号化（または署名検証）で使用する
$d$	private exponent（秘密指数）	複合化（または署名）で使用する

暗号・複合のアルゴリズム

これは式で書くととてもシンプルで、元データに対し、公開指数（$e$）・秘密指数（$d$）でべき乗し、さらにmodulus（$n$）の剰余をとる。

式にすると次のようになる（元のデータを$m$とする）。
$c = m^e \quad mod \quad n$
$m = c^d \quad mod \quad n$
署名の場合は逆に秘密鍵で署名し、公開鍵で複合する。つまり指数の部分が逆になる（$d$で署名して$e$で複合）。

ここまでをJavaで簡単に実験してみる。$p$と$q$および暗号化対象データを引数で与えて、残りは適当に決定する。パラメタを含む各種データは、必要な演算メソッドがあるBigIntegerのインスタンスとする。

SimpleRSATest.java

import java.math.BigInteger;

public class SimpleRSATest {
    public static void main(String[] args) {
        BigInteger p = new BigInteger(args[0]);
        BigInteger q = new BigInteger(args[1]);
        BigInteger m = new BigInteger(args[2]);

        //step 2. compute modulus and phi
        BigInteger n = p.multiply(q);
        BigInteger phi = p.subtract(BigInteger.ONE).multiply(q.subtract(BigInteger.ONE));
        System.out.println("modulus: " + n);
        System.out.println("phi: " + phi    );

        //step 3. determine public exponent
        System.out.println(System.currentTimeMillis() + " searching for public exponent ... ");
        BigInteger e = new BigInteger("2");
        while(! e.equals(phi)) {
            if(e.gcd(phi).equals(BigInteger.ONE)) {
                break;
            } else {
                e = e.add(BigInteger.ONE);
            }
        }
        System.out.println(System.currentTimeMillis() + " DONE! " + e);

        //step 4. determine private exponent
        System.out.println(System.currentTimeMillis() + " searching for private exponent ... ");
        BigInteger d = new BigInteger("2");
        while(! d.equals(phi)) {
            if(d.multiply(e).mod(phi).equals(BigInteger.ONE)) {
                break;
            } else {
                d = d.add(BigInteger.ONE);
            }
        }
        System.out.println(System.currentTimeMillis() + " DONE! " + d);

        //try it!
        System.out.println(System.currentTimeMillis() + " encrypting ... ");
        BigInteger enc = encrypt(m, e, n);
        System.out.println(System.currentTimeMillis() + " DONE! ");

        System.out.println(System.currentTimeMillis() + " decrypting ... ");
        BigInteger dec = encrypt(enc, d, n);
        System.out.println(System.currentTimeMillis() + " DONE! ");

        System.out.println(m + " -> " + enc);
        System.out.println(enc + " -> " + dec);
    }

    private static BigInteger encrypt(BigInteger msg, BigInteger exp, BigInteger mod) {
        return msg.modPow(exp, mod);
    }

}

BigIntegerのmodPow()メソッドを使えば、暗号化は1行で済む。暗号・複合ともアルゴリズムは同じで、渡すパラメタが異なるだけ（秘密指数を渡すか公開指数を渡すか）。

すぐに思い浮かぶ小さな素数（3,5）を使い、鍵長（$n = 15$なので4 bit）と比べて大きなデータを食わせてみると、、、

実行結果

# java SimpleRSATest 3 5 14
modulus: 15
phi: 8
1550660446376 searching for public exponent ...
1550660446376 DONE! 3
1550660446377 searching for private exponent ...
1550660446377 DONE! 3
1550660446377 encrypting ...
1550660446378 DONE! 3
1550660446378 decrypting ...
1550660446378 DONE! 3
14 -> 14
14 -> 14

なんと、暗号化しても同じ数値になってしまった。というわけで、短い鍵長では解読されやすくなるどころか、小さなデータしか暗号化できない（当然13までは普通に使える）。

pとqを自動生成（BigInteger.probablePrime()）してビット数と暗号化対象を引数指定するように変更する。

SimpleRSATest.java

        int bit = Integer.parseInt(args[0]);
        BigInteger p = BigInteger.probablePrime(bit, new Random());
        BigInteger q = BigInteger.probablePrime(bit, new Random());
        BigInteger m = new BigInteger(args[1]);

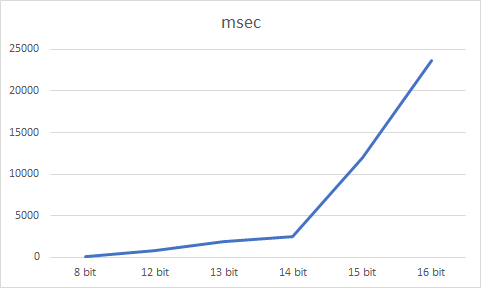
ここでbit数を変えながら秘密指数を決定するのにかかる時間をまとめた。

bit	msec	private exponent
8 bit	15	17405
12 bit	779	9667147
13 bit	1,870	23623421
14 bit	2,441	41887793
15 bit	12,006	220559501
16 bit	23,652	507694169

文字通り指数関数的に時間が伸びていっているのがわかる。2019年現在で、2048 bit以上の鍵長が安全とされているので、このプログラムに渡す引数でいえば1024 bitの2つの素数が必要となる。単純計算（上記実測での単回帰予測）でも40分以上かかることになる（実際にはもっとかかる）。

これでは使い物にならないということで、実際には以下のような手続きでこれらのパラメータが決められる。

鍵生成のステップ（実際）

1. $e$を選択する（3,5,17,257,65537から選ぶ。OpenSSLでは65537を採用している。これはフェルマー数といわれ$F_x=2^{2^x} + 1$で表される。このうち$F_0$から$F_4$は素数でそれ以降は素数ではないということが知られている、らしい。なぜこのような数値を好んで使うかといえば、ビットで表現したときに"10000000000000001"のように二つの"1"に"0"が挟まれるような並びとなり、コンピュータにとって計算しやすいから。
2. $p \quad mod \quad e \neq 1$となるような$p$を決める（必要な鍵長$\frac{k}{2}$ bit）
3. 同様に$q \quad mod \quad e \neq 1$となるような$q$を決める（$k - \frac{k}{2}$ bit）
4. $n$と$\phi$を算出する（計算方法は同じ）
5. $d$を$e$と$n$のモジュラー逆数から算出する

Javaでやってみる。

RefinedRSATest.java

import java.math.BigInteger;
import java.util.Random;

public class RefinedRSATest {

    public static void main(String[] args) {
        //step 1. select e
        BigInteger e = new BigInteger(args[0]);
        int bit = Integer.parseInt(args[1]);
        BigInteger m = new BigInteger(args[2]);
        Random r = new Random();

        //step 2. compute p where p mod e != 1
        BigInteger p;
        System.out.println(System.currentTimeMillis() + " searching for p ... ");
        while(true) {
            p = BigInteger.probablePrime(bit / 2, r);
            if(! p.mod(e).equals(BigInteger.ONE)) {
                break;
            }
        }
        System.out.println(System.currentTimeMillis() + " DONE! " + p);

        //step 3. compute q where q mod e != 1
        BigInteger q;
        System.out.println(System.currentTimeMillis() + " searching for q ... ");
        while(true) {
            q = BigInteger.probablePrime(bit - (bit / 2), r);
            if(! q.mod(e).equals(BigInteger.ONE)) {
                break;
            }
        }
        System.out.println(System.currentTimeMillis() + " DONE! " + q);

        //step 4. compute modulus and phi
        BigInteger n = p.multiply(q);
        BigInteger phi = p.subtract(BigInteger.ONE).multiply(q.subtract(BigInteger.ONE));

        //step 5. compute d from e and phi
        BigInteger d = e.modInverse(phi);

        //try it!
        System.out.println(System.currentTimeMillis() + " encrypting ... ");
        BigInteger enc = encrypt(m, e, n);
        System.out.println(System.currentTimeMillis() + " DONE! ");

        System.out.println(System.currentTimeMillis() + " decrypting ... ");
        BigInteger dec = encrypt(enc, d, n);
        System.out.println(System.currentTimeMillis() + " DONE! ");

        System.out.println(m + " -> " + enc);
        System.out.println(enc + " -> " + dec);

    }
    private static BigInteger encrypt(BigInteger msg, BigInteger exp, BigInteger mod) {
        return msg.modPow(exp, mod);
    }
}

実際に動かしてみると、さっきとは比較にならないほど速い。鍵長を2048 bitにしてもミリ秒単位で鍵生成と暗号・複合デモが完了した。ただし、AES256と同程度の強度であるといわれる15360 bitにするとさすがに時間がかかる（素数の生成に5分程度）。暗号・複合演算も、対象データが小さいにもかかわらず秒単位でかかる。
素数の選択が数打てば当たる作戦（BigInteger.probablePrime()）なのがネックになっている。openssl genrsa 15360では同じマシンで1分程度で鍵生成できた。

CRT（Chinese Remainder Theorem）を使って計算を楽にする

暗号・複合は指数計算であるため、その指数（つまり公開指数や秘密指数）の桁数（=鍵長）が大きくなるほど、文字通り指数関数的に計算量が増える（ビット長$k^3$に比例）。
そこでCRT（Chinese Remainder Theorem）というアルゴリズム（とそれに付随するパラメタ）を使うことで、秘密指数を使った処理（公開鍵暗号の複合または署名）における計算量を少なくできる、らしい。
これは暗号鍵に3つのパラメタをあらかじめ計算して保存しておき、複合の演算に使うもの。
1. dP = e.modInverse(p-1) = d.mod(p-1)
2. dQ = e.modInverse(q-1) = d.mod(q-1)
3. qInv = q.modInverse(p)

複合時は以下の計算をする。
1. m1 = c.modPow(dP, p)
2. m2 = c.modPow(dQ, q)
3. h = qInv.multiply(m1 - m2).mod(p)
4. m = m2.add(h.multiply(q))

この辺の理屈はもう偉人の知恵と思うしかない。実装してみる。

CRTRSATest.java

import java.math.BigInteger;
import java.util.Random;

public class CRTRSATest {

    public static void main(String[] args) {
        //step 1. select e
        BigInteger e = new BigInteger(args[0]);
        int bit = Integer.parseInt(args[1]);
        BigInteger m = new BigInteger(args[2]);
        Random r = new Random();

        //step 2. compute p where p mod e != 1
        BigInteger p;
        System.out.println(System.currentTimeMillis() + " searching for p ... ");
        while(true) {
            p = BigInteger.probablePrime(bit / 2, r);
            if(! p.mod(e).equals(BigInteger.ONE)) {
                break;
            }
        }
        System.out.println(System.currentTimeMillis() + " DONE! " + p);

        //step 3. compute q where q mod e != 1
        BigInteger q;
        System.out.println(System.currentTimeMillis() + " searching for q ... ");
        while(true) {
            q = BigInteger.probablePrime(bit - (bit / 2), r);
            if(! q.mod(e).equals(BigInteger.ONE)) {
                break;
            }
        }
        System.out.println(System.currentTimeMillis() + " DONE! " + q);

        //step 4. compute modulus and phi
        BigInteger n = p.multiply(q);
        BigInteger phi = p.subtract(BigInteger.ONE).multiply(q.subtract(BigInteger.ONE));

        //step 5. compute d from e and phi
        BigInteger d = e.modInverse(phi);

        //step 6. compute CRT parameters
        BigInteger dP = d.mod(p.subtract(BigInteger.ONE));
        BigInteger dQ = d.mod(q.subtract(BigInteger.ONE));
        BigInteger qInv = q.modInverse(p);

        //try it!
        System.out.println(System.currentTimeMillis() + " encrypting ... ");
        BigInteger enc = encrypt(m, e, n);
        System.out.println(System.currentTimeMillis() + " DONE! ");

        System.out.println(System.currentTimeMillis() + " decrypting ... ");
        BigInteger dec = encrypt(enc, d, n);
        System.out.println(System.currentTimeMillis() + " DONE! ");

        System.out.println(System.currentTimeMillis() + " decrypting with CRT... ");
        BigInteger dec2 = decryptWithCRT(enc, p, q, dP, dQ, qInv);
        System.out.println(System.currentTimeMillis() + " DONE! ");


        System.out.println(m + " -> " + enc);
        System.out.println(enc + " -> " + dec);
        System.out.println(enc + " -> " + dec2);

    }
    private static BigInteger encrypt(BigInteger msg, BigInteger exp, BigInteger mod) {
        return msg.modPow(exp, mod);
    }
    private static BigInteger decryptWithCRT(BigInteger c, BigInteger p, BigInteger q, BigInteger dP, BigInteger dQ, BigInteger qInv) {
        BigInteger m1 = c.modPow(dP, p);
        BigInteger m2 = c.modPow(dQ, q);
        BigInteger h = qInv.multiply(m1.subtract(m2)).mod(p);
        return m2.add(h.multiply(q));
    }
}

実行結果

java CRTRSATest 3 2048 999999999999999999999
1550668984175 searching for p ...
1550668984312 DONE! 172295263676645622090142961433941938810968859634847885352718649283943335652307381531201219791947816388624709618558064722831544819543449413413862148548502398212198232129367664537071357097143783549628019289207554523026851174626782853999027976972520323381529997253896385528709711263051313039439139827764227680119
1550668984312 searching for q ...
1550668984374 DONE! 155009203774427232415058007184226622768823333917952587100167094700260097053746651573818380802922008472261364493832345544768795940502871573671874092856361700909726970886508496382455927192820287807940406629233619377446446141580086830778212683432723563860306993510142370287498036100502589223226967052825231792047
1550668984374 encrypting ...
1550668984374 DONE!
1550668984374 decrypting ...
1550668984390 DONE!
1550668984390 decrypting with CRT...
1550668984390 DONE!
999999999999999999999 -> 999999999999999999997000000000000000000002999999999999999999999
999999999999999999997000000000000000000002999999999999999999999 -> 999999999999999999999
999999999999999999997000000000000000000002999999999999999999999 -> 999999999999999999999

何回か実行してみたが、CRTを使わない複合に5 ms程度かかっているのに対し、CRTを使用すると1 ms以内で終了していた。対象データを大きく（第3引数を長く）してみたところ、この傾向はより顕著だった。
実際に公開鍵暗号化方式を使ってデータの暗号・複合をするケースはあまりない、というか共通鍵の交換時くらいしかないかもしれない。とはいえ、CPU時間を1/3程度にできるというのはかなり魅力的だといえる。

OpenSSLでの確認

最後にOpenSSLでの鍵の内容を確認する。

openssl genrsa 512 | openssl rsa -text

実行結果抜粋

modulus:
    00:bf:80:e8:d4:ef:e4:81:b2:e8:66:fa:9f:6f:2e:
    66:ef:80:5a:fd:be:5a:39:bc:6b:74:86:43:f0:c2:
    42:0b:f6:ce:83:d8:a8:40:e3:8d:8f:42:c1:b0:d9:
    d5:ca:32:9c:e6:99:3c:d7:1e:34:e3:e9:76:26:4e:
    7e:14:61:b8:1b
publicExponent: 65537 (0x10001)
privateExponent:
    18:71:6e:c6:87:1c:26:85:dc:6e:10:7d:3b:26:b4:
    12:cb:d2:51:62:f3:87:3d:0a:86:24:01:16:00:e5:
    87:3b:2f:57:de:5c:cb:08:3d:f0:4e:4d:a7:51:03:
    e5:95:3e:67:35:a1:a1:9e:fb:75:d3:49:c5:5a:8a:
    29:50:79:19
prime1:
    00:fd:09:8c:63:c4:5b:55:7f:ef:b8:20:f2:77:05:
    e5:35:ff:37:70:ef:84:13:02:b2:b6:ca:44:49:8c:
    da:56:9f
prime2:
    00:c1:be:eb:a1:a1:ce:6c:be:20:15:5b:2f:09:9b:
    e6:b2:44:53:0c:e6:34:c5:37:b5:27:35:78:3d:88:
    07:99:05
exponent1:
    00:e5:c5:60:e5:4b:6d:c0:82:ef:34:5d:3e:af:53:
    fc:22:7f:41:61:dd:2d:2a:72:1d:c4:9c:81:4b:e4:
    8a:73:73
exponent2:
    00:88:2a:92:98:aa:8b:d5:c9:59:eb:28:86:ca:8e:
    13:79:3e:a3:cf:f1:0b:2d:80:95:84:d5:03:88:db:
    4d:db:b1
coefficient:
    00:b8:3f:8c:5d:5d:0a:d7:fe:93:b9:1e:91:a8:a2:
    b5:7c:da:3a:32:72:0f:3b:a4:c6:9f:17:9e:db:1e:
    e3:40:7f

• "prime1"と"prime2"が$p$および$q$に相当
• "modulus"が$n$（prime1*prime2）
• "publicExponent"が公開指数$e$で、前述の通り"65537"固定
• "privateExponent"が秘密指数$d$
• $\phi$は$d$の算出時にしか使わないので、鍵データに入っていない
• "exponent1"、"exponent2"、"coefficient"がそれぞれ$dP$, $dQ$, $qInv$

参考資料

RFC8017 PKCS #1: RSA Cryptography Specifications Version 2.2