目次
- はじめに
- 大数の法則とは
- 中心極限定理とは
- Rでの実装・結果確認
- 終わりに
- 参考文献・サイト
はじめに
統計学を学習あるいは活用する上で欠かせない理論の一つが中心極限定理です。
一方、同じく統計学の重要な法則として大数の法則というのも存在します。
筆者は、統計学学習時に、大数の法則と中心極限定理の違いがイマイチ理解できていませんでした。
そこで本記事では両者の違いを直感的に理解するためにRを用いた簡単なシミュレーションを行ってみようと思います。
※本記事では議論の厳密性を欠く場合がありますがご了承ください。
※なお、計算の実行環境は以下の通りです
・R version 3.6.1 (2019-07-05)
・Windows 10 Home、Intel(R) Core(TM) i5-6200U CPU @ 2.30GHz 2.40 GHz、64 ビット
大数の法則とは
サイコロを振って出る目を調べる場合を考えます。
このとき、サイコロを振るという行為は、よく試行と呼ばれます。
大数の法則とは、試行の回数を増やせば、その確率は次第に一定の値に落ち着くということ主張する法則です。
サイコロを振った際、私たちは1~6の出る目はそれぞれ1/6になると教わります。しかし、本当にそれぞれの出る目は1/6になるでしょうか。
そこで、サイコロを実際に何万回も振ってみます。すると確かに1~6の出る回数はほぼ等しくなることが分かります。
実際にRを用いて、実験を行ってみましょう(下のコードは10回サイコロを振った場合
(※2022年5月16日:コードを修正しました)
#試行回数を引数に取る関数
low_of_learge_number = function(num) {
#1から6の整数値を無作為抽出し、その結果を格納する
result = sample(6,num,replace=TRUE)
table = table(result)
return(table)
}
#グラフの描画領域を確保
par(mfrow = c(2, 3))
#グラフの描画
barplot(low_of_learge_number(10), col = "#993435", main = "n=10")
barplot(low_of_learge_number(100), col = "#993435", main = "n=100")
barplot(low_of_learge_number(1000), col = "#993435", main = "n=1000")
barplot(low_of_learge_number(10000), col = "#993435", main = "n=10000")
barplot(low_of_learge_number(100000), col = "#993435", main = "n=10000")
barplot(low_of_learge_number(1000000), col = "#993435", main = "n=100000")
サイコロを10,100,1000,10000,100000,1000000回振った時の出た目の回数は以下のようになりました。
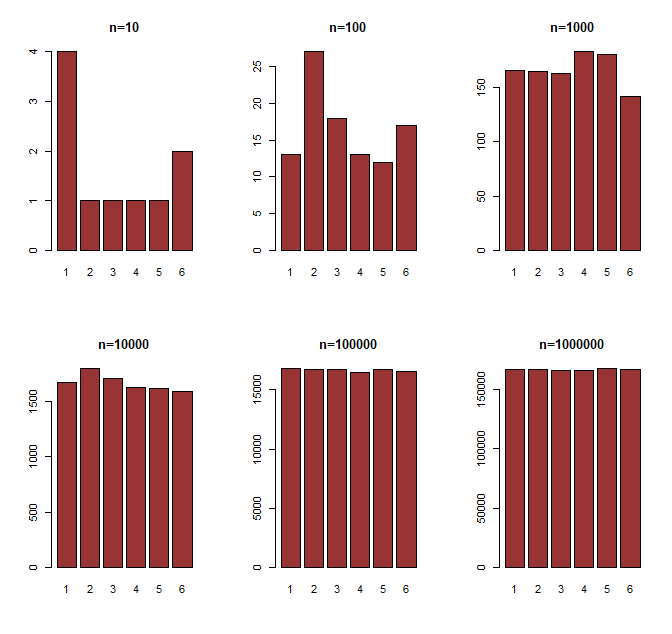
また、n=100000の時の各目の出た回数は以下のようになっています。したがって、試行回数を増やせば増やすほど、各目の出る回数が徐々に均等になっていることが分かります。このように理論的な確率と経験的な確率が次第に近づいていくということ示すことができるのですね。
x
1 2 3 4 5 6
166649 166567 166445 166618 166924 166797
中心極限定理とは
詳細な解説は割愛させていただきますが、統計的な推定や検定を行う際に非常に重要となる確率分布があります。それが、正規分布(normal distribution)と呼ばれるものです。
前提として、まず確率分布とは簡単に言うと、ある確率を返してくれる関数といえます。関数はいわゆる, y=f(x)のような数式をイメージしてください。例えば、上記のようにサイコロを振る試行を考えます。このとき、1~6までの出る目をx、またxが出る確率をP(x)としましょう(確率は英語でprobabilityなのでよくPで略記されます)。すると、1~6までの出る目の確率Pは、次のように表せます。
P(x) = 1/6 (x=1,2,3,4,5,6) (1)
では(1)の式について、グラフを描いてみましょう。
1から6までの目の出る確率は等しく1/6(=0.16...)となるように図を描くことができます。これがサイコロを振るときの確率分布となります(厳密には離散型確率分布の一種となります)。
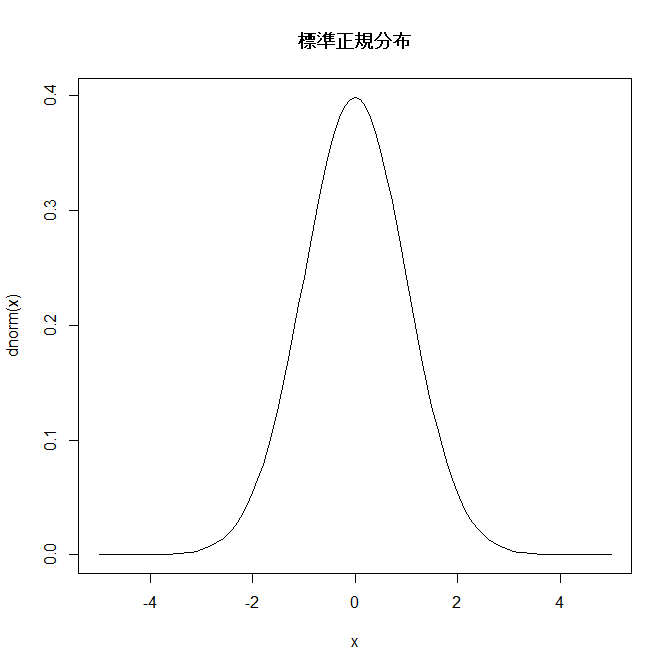
正規分布も上図のような確率分布の一種です(厳密には連続型確率分布の一種となります)。正規分布のグラフを見てみましょう。
上図が正規分布となります(厳密には平均=0, 分散=1の標準正規分布になります)。
正規分布は、「平均値付近になる確率は、両裾野付近になる確率に比べて、相対的に高い」という風に見ることができます。
具体的には、上図のx=-1から1の間に、データ全体の約68%が含まれると言われています。
つまり、ある確率分布が正規分布のような形を描くならば、ある事象が発生する確率を幅をもって推定することができるのです(幅をもって推定するとは、-0.68<=P(x)<=0.68のように確率を不等式で表すことです。区間推定と呼ばれます)。正規分布が重要であるのこのような理由があるからです。
(※2022年5月16日:以下解説、結果修正)
では、サイコロを2、5、10回振って出た目の合計値を求める操作を考えます。そして、それぞれの場合で操作を1万回繰り返します。
それぞれの場合の合計値の最小・最大値は以下のようにになりますね。
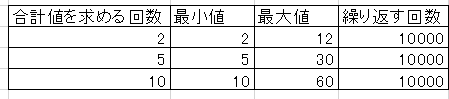
このとき、それぞれの場合において合計値の出る回数は大数の法則のように均等になるでしょうか。確認してみましょう。
Rでの実装・結果確認
以下のコードで実験を行ってみます。
clt = function (num1, num2) {
list = c()
#num1回分繰り返す
for (i in 1:num1) {
#num2回分サイコロを振る
result = sample(6, num2, replace = TRUE)
#出た目の総和を求める
total = rowSums(matrix(result, nrow = 1))
#求めた総和をベクトルに格納していく
list = c(list, total)
}
table = table(list)
return(table)
}
par(mfrow = c(3, 1))
barplot(clt(10000, 2), col = "#993435", main = "n=2")
barplot(clt(10000, 5), col = "#993435", main = "n=5")
barplot(clt(10000, 10), col = "#993435", main = "n=10")
サイコロを2、5、10回振って出た目の合計を求める作業を1万回繰り返した結果は以下のようになりました。
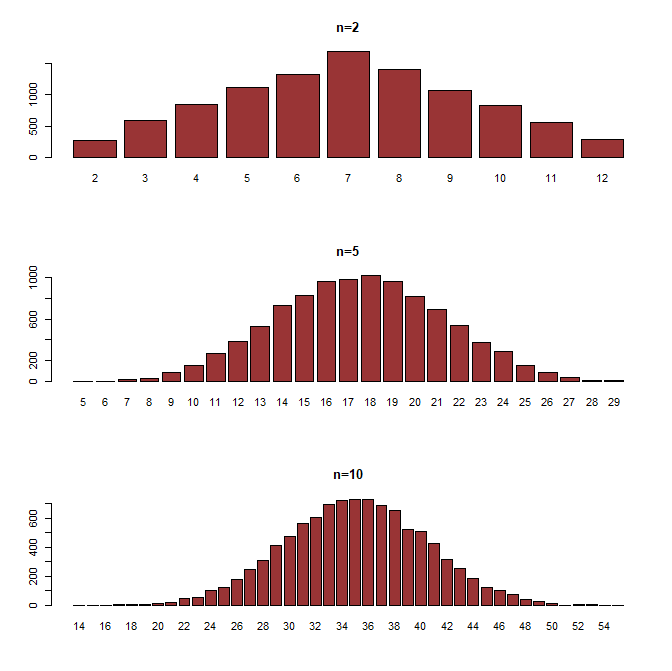
合計値を求める回数が増えるにつれて次第に正規分布に近づいていることが読み取れます。これが、中心極限定理の興味深いところです。大数の法則で確認したように、サイコロを振った時に1~6出る目の確率はそれぞれほぼ均等になります。
一方、サイコロを2、5、10回振った時の合計値の出る確率は、一様ではありません。n=10の時は、30~40辺りの値の出る確率が比較的高そうだということが読み取れます。
終わりに
以上の内容を整理しましょう。
・大数の法則:試行回数を増やすと、理論的な確率と経験的な確率が次第に近づく
・中心極限定理:一般に、母集団の確率分布が正規分布に従う場合も従わない場合も、母集団から抽出された標本の総和は、総和の項数が増えるにつれて、正規分布に従う。
(※平均値や分散も確率変数の和で表すことができるので、同様です)
参考文献・記事
[1]やさしい統計入門、田栗正章 他、講談社、2007
→統計学の基礎から応用まで丁寧に解説されています。いきなり専門書を読むのは敷居が高い人にはお勧めです。
[2]データ科学便覧 「https://data-science.gr.jp/implementation.html」
→Rでのグラフ描画関連で参考になりました。