はじめに
年始からtwitter界隈では@genkurokiさんを中心にJuliaが急激な盛り上がりを見せています。Juliaを知らない方は、@bicycle1885さんが書かれた下記の記事を参照下さい。
注目された要因は色々あるかと思いますが、何と言っても1番は処理速度ではないでしょうか。Juliaは、JIT(Just-in-time)コンパイルを行うため高速に実行できるそうです。しかし、正直な話、私はコンパイラの知識がないので、"なぜ速いか"については詳しくは分かりません。そこで簡単な数値計算を通して、Juliaの速さを体感したいと思います。
常微分方程式の数値計算
今回はこちらの常微分方程式の数値解を求める速さを比較したい思います。
\begin{aligned}
y'&= -y \\
y_0&= 1
\end{aligned}
刻み幅$h$として、前進オイラー法で離散化します。
y_{n+1} = y_{n} - y_{n} * h
$y_n$でくくります。
y_{n+1}=(1-h)y_{n}
上記の式をJuliaで書くと、
y[n+1] = (1-h)y[n]
となります。Juliaではカッコがあれば掛け算記号($*$)を省略できるので、数式とほとんど同じように書くことができます。
まずは少ない点数できちんと計算できているか確認したいと思います。
数値計算のプログラムは下記になります。点数$N$は1000点、刻み幅$h$は0.004としました。
# 点数
N = 1000
# 刻み
h = 0.004
# 初期化
y = zeros(N)
# 初期値
y[1] = 1
# 数値計算
for n = 1:N-1
y[n+1] = (1-h)y[n]
end
確認のために、数値解と解析解を比較したいと思います。上記の常微分方程式の解析解は下記になります。
f(x) = \exp(-x)
これをJuliaで書くとこうになります。
f(x) = exp.(-x)
expの後に(.)がついているのは、配列に関数を適用するためです。
またJuliaは、$f(x) = x$といった形式で関数を定義できるので、数式と同じように書くことができます。
それでは厳密解の値を求めてみます。
# x, start:step:stop
x = 0:h:(N-1)h
# 厳密解
f(x) = exp.(-x)
# y_exc
y_exc = f(x)
比較のためにプロットしてみます。Plotsというライブラリを使います。
# plot
using Plots
plot(x, y_exc)
plot!(x, y)
plot!のようにplotの後に(!)をつけると、プロットを追加することができます。ただこれでは、線が被っていてよくわからないので、線の太さ(linewidth)とスタイル(linestyle)を変更します。ついでに軸ラベル(xlabel, ylabel)もつけましょう。
# plot
using Plots
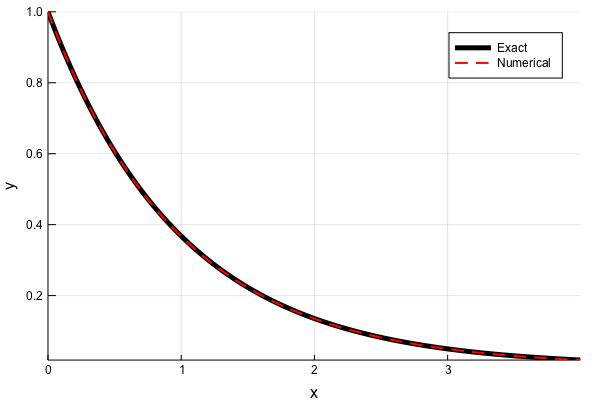
plot(x, y_exc, color=:black, linewidth=5, label="Exact",xlabel="x",ylabel="y")
plot!(x, y, color=:red, linewidth=2, linestyle=:dash, label="Numerical")
画像の保存はsavefig()です。
savefig("ODE.png")
厳密解と数値解で一致していることが確認できました。
値も見てみましょう。
@printf("%12s %12s %12s %12s\n","n" ,"Numerical" ,"Exact" , "Error")
for n = N-10:N
@printf("%12d %12.8f %12.8f %12.8e\n", n, y[n], y_exc[n], y[n]-y_exc[n])
end
出力した結果です。
n Numerical Exact Error
990 0.01898828 0.01913952 -1.51236228e-04
991 0.01891233 0.01906311 -1.50784195e-04
992 0.01883668 0.01898701 -1.50333360e-04
993 0.01876133 0.01891122 -1.49883720e-04
994 0.01868629 0.01883572 -1.49435274e-04
995 0.01861154 0.01876053 -1.48988018e-04
996 0.01853710 0.01868564 -1.48541950e-04
997 0.01846295 0.01861105 -1.48097068e-04
998 0.01838910 0.01853675 -1.47653370e-04
999 0.01831554 0.01846275 -1.47210853e-04
1000 0.01824228 0.01838905 -1.46769515e-04
誤差はありますが、同じような値になっていることが確認できました。
ここまでのコードの全文です。
# 点数
N = 1000
# 刻み
h = 0.004
# 初期化
y = zeros(N)
# 初期値
y[1] = 1
# 数値計算
for n = 1:N-1
y[n+1] = (1-h)y[n]
end
# x, start:step:stop
x = 0:h:(N-1)h
# 厳密解
f(x) = exp.(-x)
# y_exc
y_exc = f(x)
# plot
using Plots
plot(x, y_exc, color=:black, linewidth=5, label="Exact",xlabel="x",ylabel="y")
plot!(x, y, color=:red, linewidth=2, linestyle=:dash, label="Numerical")
# save
savefig("ODE.png")
# print
@printf("%12s %12s %12s %12s\n","n","Numerical","Exact","Error")
for n = N-10:N
@printf("%12d %12.8f %12.8f %12.8e\n", n, y[n],y_exc[n],y[n]-y_exc[n])
end
経過時間の計測
さて、それでは本題に移ります。経過時間の計測は@timeで出来ます。関数だけでなく、for文の頭につけることで、for文の経過時間も計測できます。
# 数値計算
@time for n = 1:N-1
y[n+1] = (1-h)y[n]
end
どうせならということで、点数は1億点、刻み幅は$40 \times 10^{-9}$に変更しました。
# 点数
N = 100000000
# 刻み
h = 0.00000004
# 初期化
y = zeros(N)
# 初期値
y[1] = 1
# 数値計算
@time for n = 1:N-1
y[n+1] = (1-h)y[n]
end
それでは、上記のファイル(ODE.jl)を実行してみましょう。
$ julia ODE.jl
31.955539 seconds (700.00 M allocations: 11.921 GiB, 1.47% gc time)
結果は約32秒となりました。参考に、同様の計算をPythonで行ってみました。
import numpy as np
import time
# 点数
N = 100000000
# 刻み
h = 0.00000004
# 初期化
y = np.zeros(N)
# 初期値
y[0] = 1
# 数値計算
start = time.time()
for n in range(N-1):
y[n+1] = (1-h)*y[n]
elapsed_time = time.time() - start
print("Elapsed Time(Python): %.2f [s]" % elapsed_time)
$ python ODE.py
Elapsed Time(Python): 41.74 [s]
結果は約42秒となりました。Pythonに比べて、Juliaの方が10秒速い程度ですね。
...というようなことをtwitterで呟いたら@bicycle1885さんに、「Juliaは、関数内に書かないと速度が出ない」と指摘して頂きました。それでは、先程のコードを関数内に書いてみましょう。
function main()
# 点数
N = 100000000
# 刻み
h = 0.00000004
# 初期化
y = zeros(N)
# 初期値
y[1] = 1
# 数値計算
@time for n = 1:N-1
y[n+1] = (1-h)y[n]
end
end
main()
先程のコードをmain()で挟んだだけです。それでは、実行してみましょう。
$ julia ODE_Function.jl
0.319719 seconds
ん? 間違えたかな、もう一度。
$ julia ODE_Function.jl
0.312822 seconds
Oh...。なんと32秒から0.31秒と、約100倍も速くなりました。
ほんとにきちんと計算できているんでしょうか。厳密解と比較してみましょう。
function main(N,h,y0)
# 初期化
y = zeros(N)
# 初期値
y[1] = y0
# 数値計算
@time for n = 1:N-1
y[n+1] = (1-h)y[n]
end
return y
end
# 点数
N = 100000000
# 刻み
h = 0.00000004
# 初期値
y0 = 1
# main
y = main(N,h,y0)
# x, start:step:stop
x = 0:h:(N-1)h
# 厳密解
f(x) = exp.(-x)
# y_exc
y_exc= f(x)
# print
@printf("%12s %12s %12s %12s\n","n","Numerical","Exact","Error")
for n = N-10:N
@printf("%12d %12.8f %12.8f %12.8e\n", n, y[n],y_exc[n],y[n]-y_exc[n])
end
実行してみます。
$ julia Julia_Compare.jl
0.318217 seconds
n Numerical Exact Error
99999990 0.01831565 0.01831565 -1.42668458e-09
99999991 0.01831564 0.01831565 -1.42668453e-09
99999992 0.01831564 0.01831565 -1.42668450e-09
99999993 0.01831564 0.01831564 -1.42668445e-09
99999994 0.01831564 0.01831564 -1.42668441e-09
99999995 0.01831564 0.01831564 -1.42668436e-09
99999996 0.01831564 0.01831564 -1.42668433e-09
99999997 0.01831564 0.01831564 -1.42668428e-09
99999998 0.01831564 0.01831564 -1.42668423e-09
99999999 0.01831564 0.01831564 -1.42668419e-09
100000000 0.01831564 0.01831564 -1.42668415e-09
きちんとできていますね!すごい!
上記の結果を表にしてみました。
| Python(参考) | Julia | Julia (Function) | |
|---|---|---|---|
| 経過時間 [s] | 41.74 | 31.96 | 0.313 |
おわりに
いかがでしたでしょうか。簡単な数値計算の結果ではありましたが、Juliaの速さを体感して頂けたでしょうか。
「Juliaだけ最適化してせこい!PythonだってnumbaやCythonを使えばもっと速くなる!」という声もあるかと思います。numbaについては試しているので、時間があればそちらの記事も書きたいと思います。
他にも、コンパイラ言語との比較も気になる所だと思います。これに関してはFortranとの比較を行いましたので、同じ時に書きたいと思います。
最後までお読み頂きありがとうございました。
環境
OS : macOS High Sierra Version 10.13.2
PC : MacBook Pro (Retina, 15-inch, Early 2013)
CPU : Intel Core i7 2.7 GHz
Memory : 16 GB 1600 MHz DDR3
Julia : 0.6.2
Python : 3.6.3
numpy : 1.13.3