概要
勤務スケジューリング問題において、複数の考慮制約があるとき、辞書式最適化が役に立つことがあります。辞書式最適化問題を解くアルゴリズムには、複数の目的関数の線形和を一度だけ最適化するものと、優先順位の高い順にひとつずつ目的関数を最適化する逐次的なものがあります。逐次的な方法を採用する際に、ある段階の最適化問題に対する最適解が、次の段階の最適化問題の実行可能解であることを利用すると、計算を高速化できることがあります。
考慮制約
勤務スケジューリング問題などの充足可能性問題では、制約条件を追加していくとほとんどの場合で問題が実行不能になります。問題が実行不能になったときの教科書的な対処方法は、考慮制約と呼ばれる制約条件を導入し、その違反度合いを目的関数とする最適化問題に帰着することです。
例えば、任意の日 $d$ に出勤する従業員の人数 $n_d$ を最低でも $m$ 人確保したいが、それが達成できないときのことを考えます。出勤する従業員数の制約条件は
\forall d \ n_d \ge m
となります。これを考慮制約にするには、足りない人数を表す決定変数 $v$ を導入し、
\begin{aligned}
\min \quad & v \\
\textrm{s.t.} \quad & \forall d \ n_d \ge m - v \\
& v \ge 0
\end{aligned}
などとします。(池上, 2018, p. 41)
複数の考慮制約の取り扱い
考慮制約が1つだけであれば問題は単純ですが、考慮制約が複数個あるときは、考慮制約間のトレードオフを考えなければなりません。例えば、従業員の希望休をできるだけ叶えたいけれど、ある日に希望が集中していて、希望を叶えると現場が回らなくなってしまう…という状況が想定されます。
$i$ 番目の考慮制約の違反度合いを $v_i$ とし、その重み付き和 $\sum_{i} w_i v_i$ を最小化する素朴なアプローチが考えられます。さて、 $w_i$ をどのように決めれば良いでしょうか? $v_i$ が1増えることの経済的な損失を $w_i$ に据えてみましょうか。「希望休を3日間分追加で叶えられるなら、1人くらい人数が足りなくなってもよい」といった交換可能条件を列挙して、それを満たすように $w_i$ を設定してもよいかもしれません。
このような方針でうまくいけばよいのですが、私の経験では、この手の話をすると業務担当者に「そんなことできません」と突っぱねられてしまいます。彼らは、何十個もある制約条件間の交換可能性や経済的価値を勘定しながら勤務スケジュールを作成しているわけではありませんから、無理からぬことです。勤務スケジューリング以外の問題でも、そうであることが多いのではないでしょうか。
しかしながら、制約条件の優先順位であれば答えてもらえることが多いです。「希望休はあくまで希望なので、円滑な事業運営を優先させたい」とか、「多少人員配置が不均衡になっても良いので、勤務間インターバルを確保したい」といった具合に、全ての制約条件が等しく扱われることは少ないでしょう。
そうした優先順位を直接的に扱う方法が辞書式最適化 (lexicographic optimization) です(和訳は私が適当にしたもので、広く使われている語ではないかもしれません)。
辞書式最適化
辞書式最適化とは、複数の目的関数を辞書式選好に基づいて最適化する問題です。辞書式選好とは、
- 最も重視する項目を比較する。それに差があるなら、良い方を選ぶ。
- 最も重視する項目に差がないなら、2番目に重視する項目を比較する。それに差があるなら、良い方を選ぶ。
- 2番目に重視する項目に差がないなら、3番目に重視する項目を比較する。それに差があるなら、良い方を選ぶ。
- 以下同様。
という手順にしたがって導かれる選好順のことです。
以下の表に示される仕事の選好順を導く例を見てみましょう。あなたは仕事の評価項目として、労働時間、給与、やりがいの3つを持っていて、労働時間は短く、給与は高く、やりがいはある仕事がよいと思っているとします。その選好は辞書式であり、労働時間 > やりがい > 給与 の順番で重視するとします。この仮定のもと、表の3つの仕事が与えられました。これらの仕事を好ましい順に並び替えるとどうなるでしょうか?
| 仕事 | 労働時間 | 給与 | やりがい |
|---|---|---|---|
| A社 | 週42時間 | 1,500万円 | あり |
| B社 | 週40時間 | 600万円 | あり |
| C社 | 週40時間 | 800万円 | なし |
上記の辞書式選好のもとでは、 B > C > A の順に好ましいという判断になります。日常的な感覚では、A社の仕事はなにやら「おいしい」匂いがしますが、上記の辞書式選好のもとでは「まず労働時間を比較して、差があるなら短いものの方が良い」と考えます。ですので、この3社のうち最も評価が低いのはA社です。ではB社とC社ではどちらが良いでしょうか?労働時間はどちらも同じなので、その次に重視しているやりがいを見ます。B社の方がやりがいがあるので、B社が最も良い、となり、前述の選好順が導かれます。
複数の目的関数があり、目的関数間に辞書的な選好があるときに、それらをまとめて最適化するにはどうしたらよいでしょうか?
辞書式最適化のアルゴリズム
ここでは、辞書式最適化のアルゴリズムとして目的関数の線形和を最適化する方法と、優先順位が高い目的関数からひとつずつ最適化していく方法を紹介します。
両者に共通の問題設定として以下を仮定します。意思決定者は $L$ 個の目的関数を持っているとし、それぞれ $f_1(x), f_2(x), \dots, f_L(x)$ とします。それらの優先順位は $f_1$ が最も高く、 $f_2, f_3, \dots$ と続くとします。辞書式最適化の目的は、与えられた選好のもとで最適な $f_1, \dots, f_L$ を与える $x$ を見つけることです。
線形和の最適化
線形和の最適化では、各目的関数 $f_i$ に重み $w_i$ を設定し、 $\sum_{i}w_i f_i(x)$ を目的関数とした単目的最適化を解きます。
なんだ、結局重みを与えなきゃいけないんじゃないかとお考えかもしれませんが、この枠組みのもとでは、重みの与え方に多少の"遊び"があります。前述の仕事を選ぶ例でいうと、労働時間が1時間減ることに対して1億円分とか1兆円分くらいの重みを与えてしまえば、給与が(現実的な範囲で)どれだけ増えようと、労働時間が少しでも短い方を選ぶことができます。その重みは、必ずしも考慮制約の経済的価値などを反映している必要はありません。辞書式の選好が実現しさえすればよいのです。
この方法の問題は、目的関数の数が多くなると、重みをとても大きくしたり小さくしたりしなければならず、数値的な問題が発生しやすくなることです。極端な例ですが、$w_L = 1$ として、優先順位が上がるごとに100倍していくよう重みを設定すると、目的関数が20個あれば $10^{40}$ くらいの重みが必要になってしまいます。1未満の重みを許容する場合でも同様に、重みの絶対値が小さくなりすぎて、優先順位が低い目的関数の変化が情報落ちで潰れてしまいます。
逐次最適化
逐次最適化では、優先順位の最も高い目的関数を最適化し、その最適値を保持しておき、次に優先順位の高い目的関数を最適化する際に、その最適値を制約条件に付与する、という手続きを繰り返します (Ogryczak et al., 2005)。以下にもう少し噛み砕いて説明します。
まずはじめに、優先順位の最も高い目的関数 $f_1$ を以下で最適化します。 $S$ は実行可能領域です。
\begin{aligned}
\min \quad & f_1(x) \\
\textrm{s.t.} \quad & x \in S
\end{aligned}
この最適化問題で得た最適解を $x_1^*$ とし、最適値 $f_1^* = f_1(x_1^*)$ を保持します。次に $f_2$ を最適化するのですが、ここで以下のように $f_1$ の値に制約をかけます。
\begin{aligned}
\min \quad & f_2(x) \\
\textrm{s.t.} \quad & x \in S \\
& f_1(x) = f_1^*
\end{aligned}
$f_2$ の最適化にあたって $f_1$ の最適性を崩さないような問題になっていますね。$f_1$ の最適化の際には他の目的関数のことを何も考慮しておらず、$f_2$ の最適化の際には $f_1$ のことだけを考慮しています。「まず $f_1$ だけを見て、それに差があるなら良い方を選ぶ。差がなければ $f_2$ を見て…」という辞書式選好の元で全体が最適化されていることが分かります。
以下同様に、 $f_1$ と $f_2$ についての制約を追加して $f_3$ を最適化します。
\begin{aligned}
\min \quad & f_3(x) \\
\textrm{s.t.} \quad & x \in S \\
& f_1(x) = f_1^* \\
& f_2(x) = f_2^*
\end{aligned}
逐次最適化は、線形和の最適化のような重みの設定を伴わないので、目的関数の数が増えても数値的な問題が発生しづらい利点があります。また、実行時間が足らず暫定解で我慢する場合でも、優先順位の高い順に目的関数が最適化されているので、どこまでが最適化されていて、どこからがされていないかの確認も容易ですから、運用上の利点も大きいと言えます。
$f_1$ を最適化する解 $x_1^*$ が $f_2$ を最適化する問題の実行可能解であることを利用すると、ソルバーによっては処理の高速化が図れます。例えばOR-ToolsのCP-SATソルバーには AddHintというメソッドがあります。ソルバーは AddHint に与えられた実行可能解を活用して、求解を高速化できることがあります。 (Dominik, 2024)。
何度も最適化問題を解くので、線形和を最適化する方法に比べて実行時間がかかるのではないかとお考えかもしれませんが、そうとは限りません。以下に実験結果を示します。
比較実験
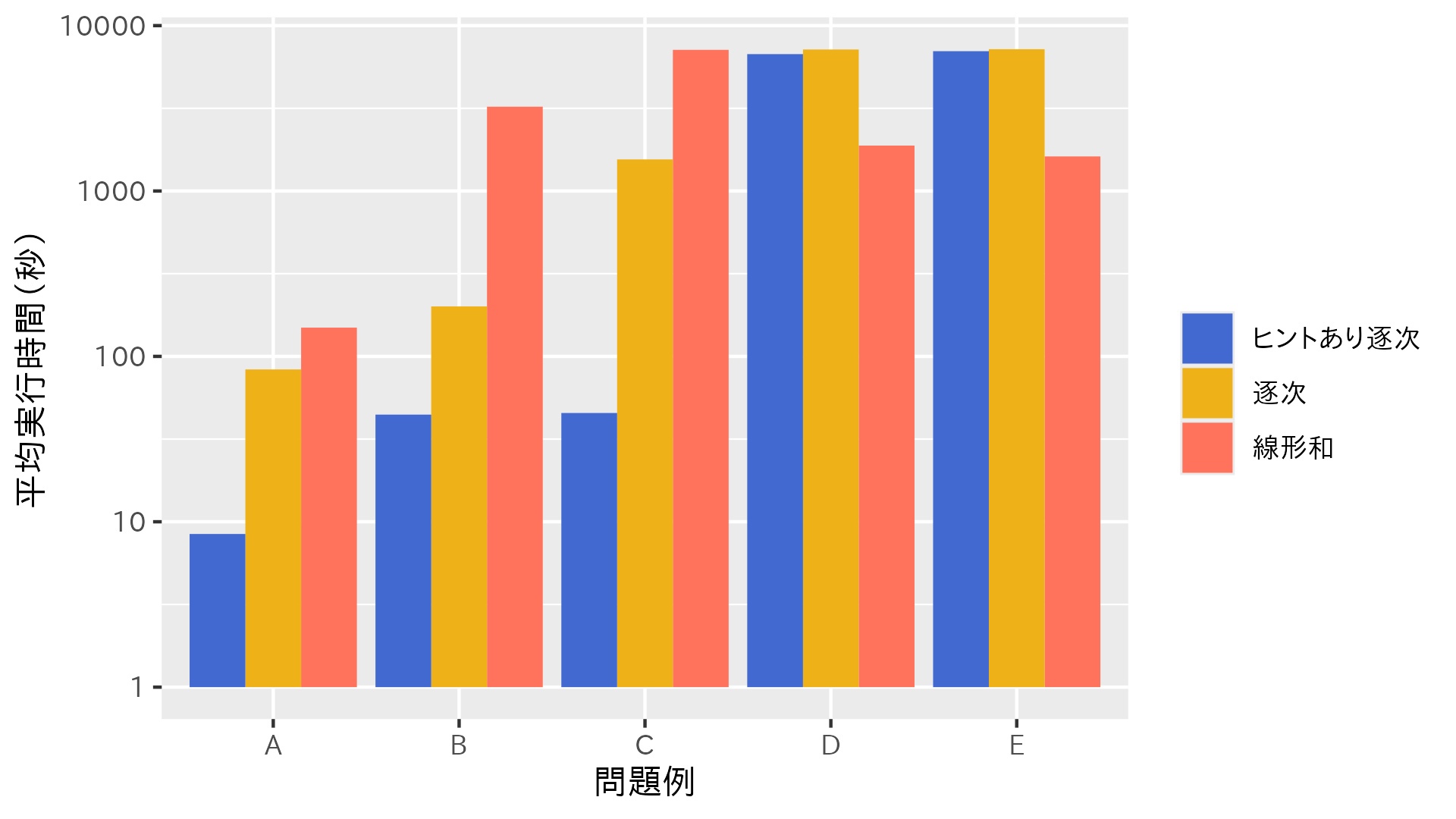
詳細はお話できませんが、私が実務で勤務スケジューリング問題における辞書式最適化の性能を検証していたときのデータを共有します(所属企業の許可は得ています)。この実験では、実際の問題例に対して、線形和の最適化、逐次最適化、ヒントあり逐次最適化の3つの求解速度を比較しました。ヒントあり逐次最適化とは、前述したCP-SATソルバーの AddHint を使った方法です。
グラフの縦軸はその問題例を64回解いたときの平均実行時間です。どの問題例でも、ヒントありの逐次最適化はヒントなしの逐次最適化より高速です。問題例A, B, Cでは、逐次最適化が線形和の最適化に比べてかなり高速になっていますが、問題例DとEでは性能が悪化しています。
このように、アルゴリズムの性能は問題例に大きく依存します。逐次最適化には運用上の利点が多いことは前述しましたが、性能上の利点が得られることもあります。