広告とかガチャとか色々なところで重みをつけてランダムに何か出したいというときがあります。こういうのを『重み付き乱択アルゴリズム』とかって言うらしいです。
こういうときによくやるのは重みの分だけ要素を用意して、配列にいれておき、要素数未満の乱数をインデックスにしてアクセスするみたいなこともよく見ます。しかしこの方法では重みは整数しか指定できません。実数で重みを指定したい場合はどうすればいいのでしょうか。
今回実装としてCPANモジュールのData::WeightedRoundRobinを参考にしました。
lib/Data/WeightedRoundRobin.pm - metacpan.org
参考にした実装では重みの合計が1である必要はありません。しかし結局重みの合計値を計算する必要があるので、合計値が1という前提にして説明します。合計値が1でない場合は重みの合計値倍すれば大丈夫です。実数値の場合、合計値が正確に1になることはほぼない(すべて2進数で表現できて、かつ極端に小さいものがない場合は大丈夫)ですが、特に問題ありません。
今回はしきい値となる値を用意します。しきい値として最初の要素に0、その後の要素のしきい値には今までの要素の重みの和を与えます。
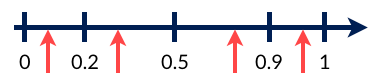
具体的に説明します。重みを0.2,0.3,0.4,0.1とします。その場合しきい値は下のようになります。
| 重み | しきい値 |
|---|---|
| 0.2 | 0 |
| 0.3 | 0.2 |
| 0.4 | 0.5 |
| 0.1 | 0.9 |
[0,1)の間の乱数を出力して、しきい値が大きい順に見ていって、用意した乱数がしきい値以上かどうかを判定します。しきい値以上ならその要素を選択するようにします。Goならrand.Float64()を使うと[0,1)の間の乱数を出力できます。
package randomized
import (
"math/rand"
"testing"
"time"
)
type weight struct {
weight float64
threshold float64
count int
}
func BenchmarkRandomized(b *testing.B) {
b.StopTimer()
lists := []*weight{&weight{weight: 0.2}, &weight{weight: 0.3}, &weight{weight: 0.4}, &weight{weight: 0.1}}
totalW := 0.0
for _, v := range lists {
(*v).threshold = totalW
totalW += v.weight
}
rand.Seed(time.Now().UnixNano())
b.StartTimer()
for i := 0; i < b.N; i++ {
random := rand.Float64()
for i := len(lists) - 1; i >= 0; i-- {
if lists[i].threshold <= random {
lists[i].count++
break
}
}
}
}
一応最初に説明した重みを整数にして重みの分だけ要素を用意する実装との速度比較をしたかったのでGoで用意してみました。
go test -bench .と実行すると比較することができます。
また要素数が増えたときは2分木探索をした方が速いです。今回参考にしたCPANモジュールのData::WeightedRoundRobinではデフォルトで要素数が10以上なら2分木探索になります。そこでどれくらいのサイズで速度は逆転するのか以前に調べました。
golang - 線形探索ではなく2分木探索した方がいいサイズってどれくらいなのか - Qiita
記事にも書いたように実際には線形探索だと最悪実行時間が長いです。2分木探索がいいのか線形探索がいいのかはアプリケーションの仕様から考えましょう。