この記事の内容
ITパスポートの試験問題はア〜エの4択問題ですが、それって偏りがあったら良くないですよね。
じゃあ本当に偏ってないかどうか、統計的に確かめましょうという話。
今回は各選択肢の出現回数の観点から確かめてみます。
データの確認
ITパスポートの過去問の正答を、こちらの記事の手順で構造化します。
出来上がったデータはこんな感じです。
# モジュールのインポート
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import chisquare
plt.rcParams['font.sans-serif'] = ['Hiragino Maru Gothic Pro', 'Yu Gothic']
%matplotlib inline
# 生データ
df.head()
| 令和4年度分 | 令和3年度分 | 令和2年度 10月分 | 令和元年度 秋期分 | 平成31年度 春期分 | 平成30年度 秋期分 | 平成30年度 春期分 | 平成29年度 秋期分 | 平成29年度 春期分 | 平成28年度 秋期分 | 平成28年度 春期分 | 平成27年度 秋期分 | 平成27年度 春期分 | 平成26年度 秋期分 | 平成26年度 春期分 | 平成25年度 秋期分 | 平成25年度 春期分 | 平成24年度 秋期分 | 平成24年度 春期分 | 平成23年度 秋期分 | 平成23年度 特別分 | 平成22年度 秋期分 | 平成22年度 春期分 | 平成21年度 春期分 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | エ | ウ | ウ | エ | エ | ア | エ | ウ | ア | エ | ア | ア | ウ | ウ | ア | エ | ア | エ | イ | ア | ア | エ | ア | ウ |
| 1 | イ | エ | イ | ア | ウ | ウ | ウ | エ | イ | ア | ア | ア | ア | ウ | エ | ア | ウ | イ | ア | イ | イ | ア | イ | ウ |
| 2 | ウ | ウ | イ | ウ | ア | ウ | イ | ア | ア | ウ | エ | エ | エ | ア | エ | エ | イ | ア | イ | エ | イ | イ | エ | イ |
| 3 | ア | ア | ウ | エ | イ | ウ | ア | イ | イ | エ | ウ | ア | ウ | イ | イ | ウ | ア | イ | ア | エ | イ | ア | ウ | ア |
| 4 | イ | ウ | イ | エ | ア | ウ | イ | ア | イ | イ | ウ | ア | ア | ウ | エ | ウ | エ | イ | ウ | イ | ウ | ウ | イ | イ |
仮説 : ア〜エの選択肢の出現回数はランダムだと言えるのか?
特定の選択肢が正解になりやすいという事があれば試験として問題ですね。
逆に全ての選択肢が同じ数だけ出現するというのも、メタ読みで正解が分かってしまうので良くないです。
なので理想は、サイコロで決めるように全ての選択肢が正解になる確率が等しい事です。
つまり、各選択肢の出現回数は一様分布に従うべきです。
データの出現回数が特定の分布に従うことを検証するためには、カイ2乗検定を行います。
それでは、ITパスポートの過去の試験が一様分布に従うかどうか、カイ2乗検定で確かめてみます。
有意水準は5%で。
データの変換
まずは集計しやすいようにデータを縦持ちに変換します。
df_long = df.unstack()
df_long.name = "value"
df_long = df_long.reset_index()
df_long.head()
| level_0 | level_1 | value | |
|---|---|---|---|
| 0 | 令和4年度分 | 0 | エ |
| 1 | 令和4年度分 | 1 | イ |
| 2 | 令和4年度分 | 2 | ウ |
| 3 | 令和4年度分 | 3 | ア |
| 4 | 令和4年度分 | 4 | イ |
続いて各試験ごとに4つの選択肢それぞれが正解となった回数を集計します。
count = df_long.groupby("level_0")["value"].value_counts().unstack().loc[df.columns]
count.head()
| value | ア | イ | ウ | エ |
|---|---|---|---|---|
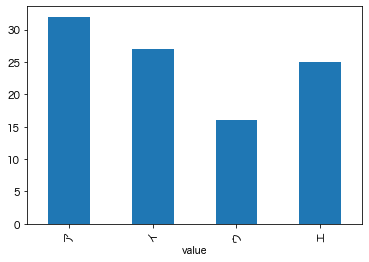
| 令和4年度分 | 32 | 27 | 16 | 25 |
| 令和3年度分 | 29 | 20 | 25 | 26 |
| 令和2年度 10月分 | 27 | 25 | 23 | 25 |
| 令和元年度 秋期分 | 21 | 20 | 23 | 36 |
| 平成31年度 春期分 | 26 | 22 | 26 | 26 |
例えば令和4年度分の試験の選択肢はこんな分布です。
count.loc["令和4年度分"].plot.bar()
plt.show()
比較対象データの作成
次に、比較対象となる期待される出現回数を用意します。
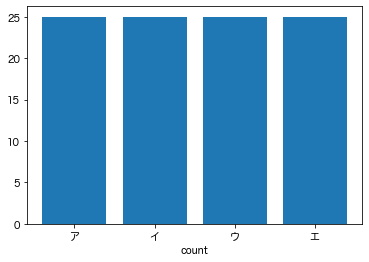
選択肢が4つ、問題が100問なので全ての選択肢が25回出現することが期待されます。
f_exp_count = np.ones(4, dtype=int) * 25
plt.bar(count.columns, f_exp_count)
plt.xlabel("count")
plt.show()
カイ2乗検定の実行
あとは各行に一様分布とのカイ2乗検定を行い、p値を取り出せば分析完了です。
count.apply(lambda x:chisquare(x, f_exp_count).pvalue, axis=1)
令和4年度分 0.147256
令和3年度分 0.641389
令和2年度 10月分 0.956224
令和元年度 秋期分 0.084302
平成31年度 春期分 0.923263
平成30年度 秋期分 0.539870
平成30年度 春期分 0.539870
平成29年度 秋期分 0.221385
平成29年度 春期分 0.004551
平成28年度 秋期分 0.714937
平成28年度 春期分 0.397834
平成27年度 秋期分 0.288573
平成27年度 春期分 0.361805
平成26年度 秋期分 0.180798
平成26年度 春期分 0.849467
平成25年度 秋期分 0.696186
平成25年度 春期分 0.868490
平成24年度 秋期分 0.270233
平成24年度 春期分 0.641389
平成23年度 秋期分 0.009222
平成23年度 特別分 0.606269
平成22年度 秋期分 0.200137
平成22年度 春期分 0.288573
平成21年度 春期分 0.119659
dtype: float64
結論
カイ2乗検定の帰無仮説は、2つの分布が同じであることなので、p値が有意水準を上回っていれば選択肢がランダムに決められていると考えても差し支えないということになります。
結果を見ると、H23年秋とH29年春はp値が有意水準5%を下回っているので怪しいですね。
予告
次の記事では、同じ選択肢が連続で正解になることの調整がされているか、確認していきます。