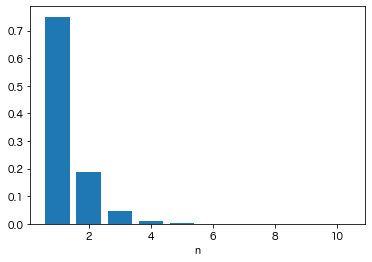この記事の内容
ITパスポートの試験問題はア〜エの4択問題ですが、それって偏りがあったら良くないですよね。
じゃあ本当に偏ってないかどうか、統計的に確かめましょうという話。
同じ選択肢が連続で正解になることの調整がされているか、という観点で確認してみます。
前回はこちら
仮説 : ア〜エの選択肢の出現回数はランダムだと言えるのか?
選択問題を解いていて同じ選択肢が連続すると、ちょっと不安になりますよね。(アが3回連続になってる!みたいな感じ)
それって出題側からしても同じだと思うんです。なるべく連続しないようにしようとか、逆にその真理を逆手にとって連続させようとか。
でもそんな考えでバイアスが掛かった順番にするのは公正ではないですね。(ここではそう思ってください)
そこで、ITパスポート試験で同じ選択肢が連続で正解になる回数が、ランダムな系列と同様の分布になっているのか調べていきます。
ランダムな系列の連続出現回数の分布
選択が完全にランダムな場合、$m$個の選択肢の中から同じ選択肢が連続で$n$回選ばれる確率$p(m,n)$は次のように書けます。
二項分布と似ていますがちょっと違いますね。
$$
p(m,n) = \frac{1}{m^{n-1}}(1-\frac{1}{m})
$$
まず最初の1回目は何が出てもいいですが、次からは$n-1$回同じ選択肢が選ばれ続けるので$\frac{1}{m^{n-1}}$が出てきます。$n=1$の時はこの部分は$1$になります。
$n$回連続で同じ選択肢が出た次の選択では、逆に今までと違う選択肢が選ばれなければいけないので余事象の確率$(1-\frac{1}{m})$が出てきます。
この確率分布はおそらくPythonで実装されていなそうなので、自分で定義しておきます。
import numpy as np
m = 4
dist_func = np.frompyfunc(lambda n,m: 1/(m**(n-1)) * (1-1/m), 2, 1)
確率分布は、指数関数を左右逆にしたような形です。
この確率分布とデータを比べる事で、正解選択肢の出現順に作為がないのか確かめます。
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['Hiragino Maru Gothic Pro', 'Yu Gothic']
%matplotlib inline
n_list = np.arange(1,11)
m = 4
prob = dist_func(n_list,m)
plt.bar(n_list, prob)
plt.show()
データの変換
前回と同様、ITパスポートの過去問の正答を、こちらの記事の手順で構造化したデータを使います。
今回はア〜エの文字ではなく、数値化したデータを使います。
df_num.head()
| 令和4年度分 | 令和3年度分 | 令和2年度 10月分 | 令和元年度 秋期分 | 平成31年度 春期分 | 平成30年度 秋期分 | 平成30年度 春期分 | 平成29年度 秋期分 | 平成29年度 春期分 | 平成28年度 秋期分 | 平成28年度 春期分 | 平成27年度 秋期分 | 平成27年度 春期分 | 平成26年度 秋期分 | 平成26年度 春期分 | 平成25年度 秋期分 | 平成25年度 春期分 | 平成24年度 秋期分 | 平成24年度 春期分 | 平成23年度 秋期分 | 平成23年度 特別分 | 平成22年度 秋期分 | 平成22年度 春期分 | 平成21年度 春期分 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 3 | 2 | 2 | 3 | 3 | 0 | 3 | 2 | 0 | 3 | 0 | 0 | 2 | 2 | 0 | 3 | 0 | 3 | 1 | 0 | 0 | 3 | 0 | 2 |
| 1 | 1 | 3 | 1 | 0 | 2 | 2 | 2 | 3 | 1 | 0 | 0 | 0 | 0 | 2 | 3 | 0 | 2 | 1 | 0 | 1 | 1 | 0 | 1 | 2 |
| 2 | 2 | 2 | 1 | 2 | 0 | 2 | 1 | 0 | 0 | 2 | 3 | 3 | 3 | 0 | 3 | 3 | 1 | 0 | 1 | 3 | 1 | 1 | 3 | 1 |
| 3 | 0 | 0 | 2 | 3 | 1 | 2 | 0 | 1 | 1 | 3 | 2 | 0 | 2 | 1 | 1 | 2 | 0 | 1 | 0 | 3 | 1 | 0 | 2 | 0 |
| 4 | 1 | 2 | 1 | 3 | 0 | 2 | 1 | 0 | 1 | 1 | 2 | 0 | 0 | 2 | 3 | 2 | 3 | 1 | 2 | 1 | 2 | 2 | 1 | 1 |
ここから正解選択肢が連続した回数を数えていきますが、結構複雑な変換が必要です。
まず令和4年度分の原系列を見てみます。8→9のところで同じ選択肢が連続していますね。
df_num.head(10)["令和4年度分"]
0 3
1 1
2 2
3 0
4 1
5 2
6 1
7 3
8 0
9 0
Name: 令和4年度分, dtype: int64
この連続を見つけるために、以下の手順で変換していきます。
-
diffで前後の値の差分に変換 -
cumsumで値が変化した回数を足し上げる- ここで、値の変化がない(同じ選択肢が連続してる)時は同じ値が連続した回数分並ぶ
-
unstackでグループ処理しやすいように縦持ちにする
ここまですると、次のように同じ選択肢が連続した部分(8→9のところ)で同じ数が並ぶようになります。
df_change_cumsum = (df_num.diff() != 0).cumsum().unstack()
df_change_cumsum.name = "value"
df_change_cumsum = df_change_cumsum.reset_index()
df_change_cumsum.head(10)
| level_0 | level_1 | value | |
|---|---|---|---|
| 0 | 令和4年度分 | 0 | 1 |
| 1 | 令和4年度分 | 1 | 2 |
| 2 | 令和4年度分 | 2 | 3 |
| 3 | 令和4年度分 | 3 | 4 |
| 4 | 令和4年度分 | 4 | 5 |
| 5 | 令和4年度分 | 5 | 6 |
| 6 | 令和4年度分 | 6 | 7 |
| 7 | 令和4年度分 | 7 | 8 |
| 8 | 令和4年度分 | 8 | 9 |
| 9 | 令和4年度分 | 9 | 9 |
続いて次の手順で連続回数を数え上げます。
-
groupbyで試験毎の集計を行う -
value_countsで各値ごとの出現回数(=同じ選択肢が連続した回数)を数え上げる - 再び
value_countsで「同じ選択肢が連続した回数」の回数を数え上げる
これで、同じ選択肢が連続した回数の頻度がわかります。
cont = df_change_cumsum.groupby("level_0")["value"].value_counts(sort=False)
cont.name = "count"
cont = cont.reset_index("level_0").value_counts().unstack(fill_value=0).loc[df.columns]
cont
| count | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| 令和4年度分 | 50 | 14 | 3 | 2 | 1 | 0 | 0 |
| 令和3年度分 | 57 | 15 | 3 | 1 | 0 | 0 | 0 |
| 令和2年度 10月分 | 51 | 13 | 5 | 2 | 0 | 0 | 0 |
| 令和元年度 秋期分 | 58 | 17 | 0 | 2 | 0 | 0 | 0 |
| 平成31年度 春期分 | 58 | 17 | 1 | 0 | 1 | 0 | 0 |
| 平成30年度 秋期分 | 44 | 10 | 8 | 3 | 0 | 0 | 0 |
| 平成30年度 春期分 | 62 | 11 | 2 | 0 | 2 | 0 | 0 |
| 平成29年度 秋期分 | 48 | 15 | 1 | 1 | 3 | 0 | 0 |
| 平成29年度 春期分 | 58 | 7 | 8 | 1 | 0 | 0 | 0 |
| 平成28年度 秋期分 | 59 | 13 | 5 | 0 | 0 | 0 | 0 |
| 平成28年度 春期分 | 60 | 15 | 2 | 1 | 0 | 0 | 0 |
| 平成27年度 秋期分 | 56 | 12 | 2 | 1 | 2 | 0 | 0 |
| 平成27年度 春期分 | 54 | 10 | 6 | 2 | 0 | 0 | 0 |
| 平成26年度 秋期分 | 52 | 18 | 4 | 0 | 0 | 0 | 0 |
| 平成26年度 春期分 | 48 | 16 | 3 | 1 | 0 | 0 | 1 |
| 平成25年度 秋期分 | 57 | 14 | 5 | 0 | 0 | 0 | 0 |
| 平成25年度 春期分 | 69 | 11 | 3 | 0 | 0 | 0 | 0 |
| 平成24年度 秋期分 | 60 | 15 | 2 | 1 | 0 | 0 | 0 |
| 平成24年度 春期分 | 48 | 17 | 6 | 0 | 0 | 0 | 0 |
| 平成23年度 秋期分 | 53 | 18 | 2 | 0 | 1 | 0 | 0 |
| 平成23年度 特別分 | 48 | 19 | 2 | 2 | 0 | 0 | 0 |
| 平成22年度 秋期分 | 60 | 13 | 2 | 2 | 0 | 0 | 0 |
| 平成22年度 春期分 | 56 | 18 | 1 | 0 | 1 | 0 | 0 |
| 平成21年度 春期分 | 57 | 14 | 3 | 0 | 0 | 1 | 0 |
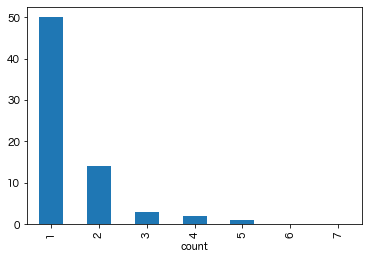
例えば令和4年なら、連続回数が1回(=前後が違う選択肢)の箇所が50、2連続で同じ選択肢の箇所が14、という風になっています。
分布の形状を見ると、確かに予想していた分布に近いですね。
cont.T["令和4年度分"].plot.bar()
plt.show()
カイ2乗検定の実行
あとは前回と同様、カイ2乗検定でp値を取り出せばいいのですが、2点問題があります。$n$の定義域と試行回数です。
原理上、$n$は$\infty$まで取り得ますが、ITパスポートの問題は100問なので、$n$の定義域は$1\le n \le 100$です。ただ、そうすると確率の積分が1にならないので、上で定義した確率の式をそのまま使えません。
さらに、カイ2乗検定をするためには比較対象分布の頻度を作る必要がありますが、問題数が100問という制約があるため試行回数が毎回異なってしまうのです。(100問同じ選択肢が正解なら試行数は1回、100問全て連続しない選択肢が正解なら試行数は100回)
ここら辺を厳密にしすぎるとかなり複雑な式になりそうなので、今回は近似的にちょうどいいところで$n$を打ち切るようにします。あまり小さい値で打ち切ってしまうと確率の積分が1にならないと怒られるので、$1\le n \le 15$くらいで打ち切ってみます。$1\le n \le 100$にしても良いのですが、0しか入っていないデータを大量に入れると識別性が不当になりそうなので、小さめの値にしてみました。15という値はエイヤで決めました。
また、試行回数については実際にデータとして得られた頻度の合計を試行回数として逆算することにします。こうすると期待頻度から計算した問題数が100問にならない事がありますが、今回は目を瞑ります。
この辺について、うまいやり方があるかも知れないですが思いつきませんでした。コメントでアイデア頂けると嬉しいです。
ということで、この条件の元でカイ2乗検定を行ってp値を取得する関数を作り、applyで各行に適用してp値の一覧を取得します。
def chi_test(x,dist_func=dist_func, m=4, n_cutoff=15):
f_obs = np.append(x, np.zeros(n_cutoff - len(x)))
f_exp = x.sum() * dist_func(np.arange(n_cutoff) + 1, m)
res = chisquare(f_obs, f_exp)
return res.pvalue
cont.apply(lambda x:chi_test(x, n_cutoff=15),axis=1)
令和4年度分 9.851389e-01
令和3年度分 1.000000e+00
令和2年度 10月分 9.992976e-01
令和元年度 秋期分 9.734678e-01
平成31年度 春期分 9.670341e-01
平成30年度 秋期分 3.296057e-01
平成30年度 春期分 2.678962e-01
平成29年度 秋期分 1.446884e-04
平成29年度 春期分 7.803837e-01
平成28年度 秋期分 9.999375e-01
平成28年度 春期分 9.999980e-01
平成27年度 秋期分 3.232313e-01
平成27年度 春期分 9.882266e-01
平成26年度 秋期分 9.995129e-01
平成26年度 春期分 5.413938e-11
平成25年度 秋期分 9.999606e-01
平成25年度 春期分 9.975446e-01
平成24年度 秋期分 9.999980e-01
平成24年度 春期分 9.884849e-01
平成23年度 秋期分 9.728506e-01
平成23年度 特別分 9.795322e-01
平成22年度 秋期分 9.996105e-01
平成22年度 春期分 9.514351e-01
平成21年度 春期分 2.323815e-01
dtype: float64
結論
H26年春とH29年秋が、p値がかなり小さいですね。
H26春は7回連続が出てきている点、H29秋は5回連続が3箇所もあった点がその原因だと思います。
第一種の過誤の可能性はありますが、これだけ小さいp値が24回中2回も現れるのはちょっと怪しい気もしますね。
あとは、ランダムだと思って良さそうなんですが、90%代の大きなp値の試験が多いので逆に不自然ですね。
もしかすると同じ選択肢が正解にならないような作為が行われているかもしれません。
(@WolfMoon さんの前回の記事の指摘からヒントを得ました。ありがとうございます。)