ゼロから作るDeep Learning 4.3.3 偏微分 のサンプルコードを元に独自の関数の勾配ベクトルを描画してみる。

はじめに

4.3.3 偏微分では、f = x0^2 + x1^2 の勾配ベクトルを描画する例がコードとともに説明されています。
これをもとに、f = x0 * x1 の結果を描画しようとしたときに、はまったので解決策を記載します。
元のサンプルコードはdeep-learning-from-scratch/ch04/gradient_2d.pyです。
実行結果は以下のようになります。

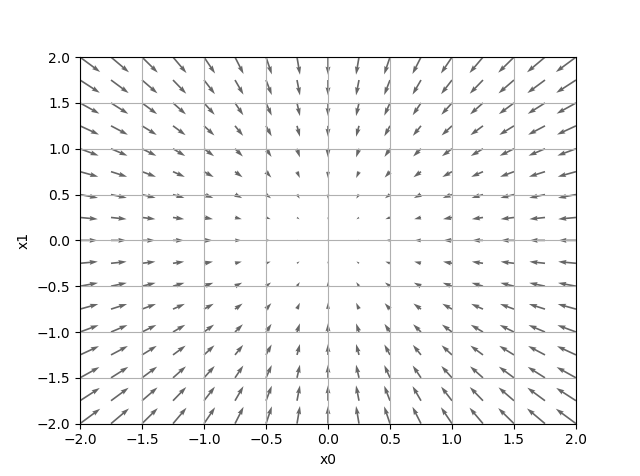
検証

まず最初に今回の検証結果コードを示します。

# coding: utf-8
# cf.http://d.hatena.ne.jp/white_wheels/20100327/p3
import numpy as np
import matplotlib.pylab as plt
from mpl_toolkits.mplot3d import Axes3D

def _numerical_gradient_no_batch(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x)
    
    for idx in range(x.size):
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = f(x) # f(x+h)
        
        x[idx] = tmp_val - h 
        fxh2 = f(x) # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)
        
        x[idx] = tmp_val # 値を元に戻す
        
    return grad


def numerical_gradient(f, X):
    if X.ndim == 1:
        return _numerical_gradient_no_batch(f, X)
    else:
        grad = np.zeros_like(X)
        
        for idx, x in enumerate(X):
            grad[idx] = _numerical_gradient_no_batch(f, x)
        
        return grad

def function_2(x):
    if x.ndim == 1:
        return np.sum(x**2)
    else:
        return np.sum(x**2, axis=1)

# f = x0*x1, df/dx0 = x1, df/dx1 = x0
# can110
def function_xy(x):
    if x.ndim == 1:
        return x[0]*x[1]
    else:
        return x[:,0]*x[:,1]

# f = sin(x0*x1), df/dx0 = x1*cos(x0*x1), df/dx1 = x0*cos(x0*x1)
# can110
def function_sin_xy(x):
    if x.ndim == 1:
        return np.sin(x[0]*x[1])
    else:
        return np.sin(x[:,0]*x[:,1])

def tangent_line(f, x):
    d = numerical_gradient(f, x)
    print(d)
    y = f(x) - d*x
    return lambda t: d*t + y
     
if __name__ == '__main__':
    x0 = np.arange(-2, 2.5, 0.25)
    x1 = np.arange(-2, 2.5, 0.25)
    X, Y = np.meshgrid(x0, x1)
    
    X = X.flatten()
    Y = Y.flatten()
    a = np.array([X, Y])
    a = a.T # 転置。１行=１ベクトル（列=x0, x1）であるべき can110

    # 検証
    #func = function_2      # df/dx0(=2*x0), df/dx1(=2*x1)は、それぞれx0,x1のみから算出されるので、たまたまうまくいっている？
    func = function_xy
    #func = function_sin_xy
    
    #grad = numerical_gradient(function_2, np.array([X, Y]) )
    grad = numerical_gradient(func, a)
    grad = grad.T # quiverのために転置（行毎にx0,x1座標値を配置） can110
    
    plt.figure()
    plt.quiver(X, Y, -grad[0], -grad[1],  angles="xy",color="#666666")#,headwidth=10,scale=40,color="#444444")
    plt.xlim([-2, 2])
    plt.ylim([-2, 2])
    plt.xlabel('x0')
    plt.ylabel('x1')
    plt.grid()
    plt.legend()
    plt.draw()
    plt.show()

今回、f = x0 * x1関数を以下のように定義しました。ちなみに今回の勾配算出ではx.ndim == 1の部分だけ呼ばれます。

def function_xy(x):
    if x.ndim == 1:
        return x[0]*x[1]
    else:
        return x[:,0]*x[:,1]

これを元のfunction_2と置き換えて実行しましたが、なにやらおかしな結果に。

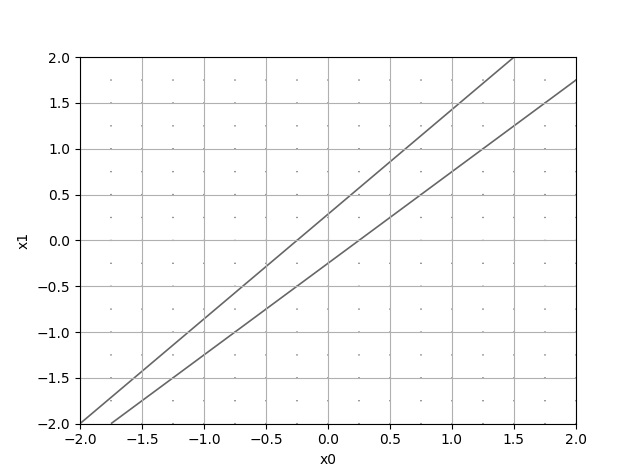
そこで実際の勾配の計算コードを追ってみました。
numerical_gradient関数で複数ベクトル分→_numerical_gradient_no_batch関数で１ベクトル分の勾配を計算しています。
そこで_numerical_gradient_no_batchでのx.shapeを見てみると**(324,)。ベクトル（描画する点）の数です。
ここは本来(2,)**となるべき。いうことで、呼出元を確認すると

    grad = numerical_gradient(function_2, np.array([X, Y]) )

X(x0)とY(x1)座標の組を渡してます。これが原因ですね。np.array([X, Y]を転置し１行＝１ベクトル（点）の形にすることで正しく描画されるようになりました。

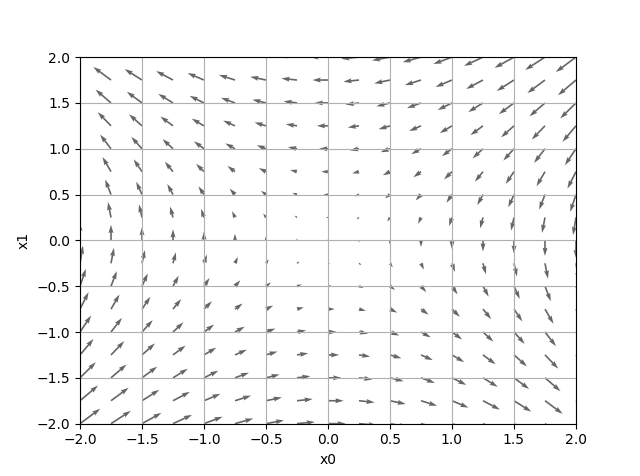
まとめ

• numerical_gradient関数には、転置した結果（１行=１ベクトル）を渡す。
• numerical_gradientの結果もquiver描画のために転置（行毎にx0,x1座標値を配置）する。

『ゼロから作る Deep Learning』の正誤表にも特に記載なかったですが、バグのような？