ヨビノリたくみさんの動画「期待値が無限大な賭け(サンクトペテルブルクのパラドックス)」を見て面白そうだったのでシミュレーションしてみました。
問題設定
問題のゲームは、
確率1/2のコインを表が出るまで投げて、k回目に表が出たら2^(k-1)円賞金がもらえるというゲームです。
例えば、裏裏裏表、つまり4回目に表が出たら
2^(4-1) = 8 (円)
になります。
このゲーム、半分の確率で1円、1000円以上もらえる確率は0.1%にも満たない。
一回10万円でできると言われても絶対にやりたくない賭けなんですが、
期待値を計算すると無限大で、明らかに直感に反しています。
この問題を解決するために様々な方法が考えられましたが、
ウィリアム・フェラーは「標本抽出」という統計学の概念を用いました。
期待値は「母集団の平均値」であり、実際に獲得する賞金額は「標本平均」であると考えることで、
参加回数nによって標本平均が変化することを示しました。
シミュレーション
今回シミュレーションするのは、冒頭の動画の20:30くらいから描いているグラフです。
n回参加するときの一回当たりの獲得賞金はnを大きくするとlog2(n)に近づく(正確には確率収束)らしいのでやってみます。
# サンクトペテルブルクのパラドックス
# 賞金を出力する関数を作る
reward <- function(){
k <- 0 # 試行回数のカウント
result <- 0 # コイン投げの結果:0を裏、1を表とする
## 成功するまで処理を繰り返す
while (result == 0) {
k <- k + 1
## コイン投げ
result <- sample(0:1, size = 1, replace = TRUE, prob = c(0.5, 0.5))
}
return(2^(k-1)) # 賞金
}
# 賭けをやってみよう
cat("賞金は", reward(), "円")
# >>賞金は 2 円
# 賭けにn回参加した時の一回当たりの利得(S(n)/n)を計算する関数
rew_per_game <- function(n){
S_n <- 0 # 合計利得
for (i in 1:n){
S_n <- S_n + reward()
}
return(S_n/n)
}
# グラフ描画
plotGraph <- function(m, n, ylim, by){
par(new =F) # 新しいグラフを描画
plot(log2(0:n+1), type = "l", col = "red", xlim = c(0,n+1), ylim = c(0,ylim),
xlab = '', ylab = '', pch = 20) # 理論値log2(n)のグラフ
par(new = TRUE) # 次に描画するグラフを重ねる
part = seq(1,n+1,by=by) # シミュレーションする参加回数のベクトル
df <- data.frame(part = part, rew_per_game = 0, mean = 0) # シミュレーション結果を入れるデータフレーム
for(i in 1:m){
df <- data.frame(part = part, rew_per_game = 0, mean = df$mean) # データフレームの初期化
df$rew_per_game <- lapply(df$part ,rew_per_game) # 各参加回数に対してシミュレーション
plot(df$part, df$rew_per_game, xlim = c(0,n+1), ylim = c(0,ylim), pch = 20, cex = 0.01,
xlab = '', ylab = '', axes = FALSE) # 結果のプロット
par(new = TRUE)
df$mean <- unlist(df$mean) + unlist(df$rew_per_game)/m # 平均値の計算
}
plot(df$part, df$mean, type = "b", col = "blue", xlim = c(0,n+1), ylim = c(0,ylim),
xlab = '', ylab = '') # 平均値のグラフ
}
# パラメータの設定
m = 10 # サンプル数
n = 1000 # 参加回数をn回まで描画
ylim = 30 # y軸最大値の設定
by = 100 # 参加回数何回ごとにシミュレーションするか
plotGraph(m, n, ylim, by)
m, n, ylim, by のパラメータをいじることでいろいろ遊べます。
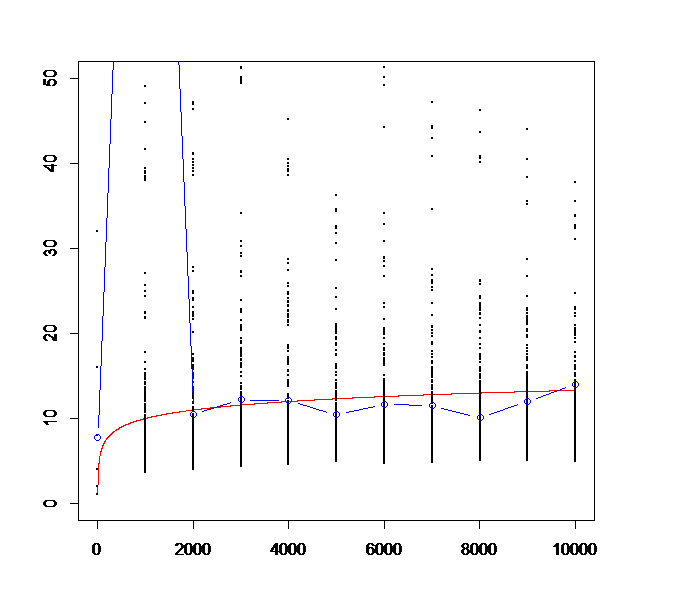
↑これはm=500, n=10000, ylim=50, by=1000
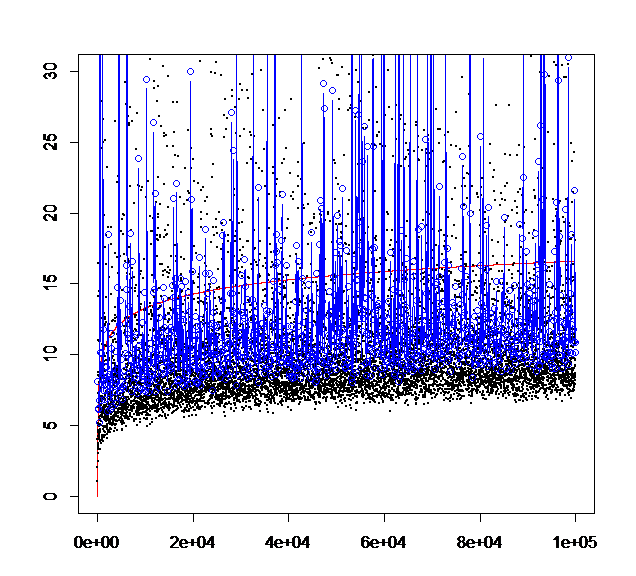
↑時間かかりますがこんなのもできます(m=10, n=100000, ylim=30, by = 100)
実際にシミュレーションするとばらつきが大きすぎて全然結果が安定しないことが実感できます。
ところでこれ、mを増やしたら一回当たりの獲得賞金も増えてしまうように思えるんですがどうなんでしょうか。