現場で潰しが効くディープラーニング講座

線形代数学(行列～特異値分解)

１、行列の計算
　・スカラー倍⇒行列の各成分に一つのスカラーを掛けること
　・行列の積は可換でない　　⇒　　A・B≠B・A
　・行列の積は結合的である　⇒　（ A・B)・C = A・(B・C)
・行列の乗法は加法の上に分配的である　⇒(A+B)・C=A・C+B・C および A・(B+C)=A・B+A・C
２、行列式の求め方
　・各成分の余因子で計算する方法
３、逆行列の求め方
　・行列式と余因子行列で計算する
　・掃き出し法で逆行列を求める
４、固有値・固有ベクトル 求め方
　・｜Ａ-λＩ｜＝０にって方程式で求める
５、固有値分解
　・正方形の行列を３つの行列の積に変換することを固有値分 解という。この変換によって行列の累乗の計算が容易になる等の利点がある。
６、特異値分解
　・正方行列以外は固有値分解。これを利用して画像のデータ量を小さくすることできる。

統計学（集合、確率、統計）

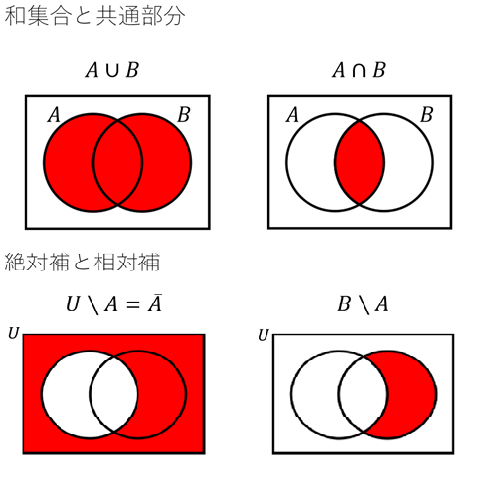
１、集合

２、確率
　・確率の定義　　⇒P(A)=事象A起こる数/すべての事象の数　　P(A）は０～１の間の値をとる
　・ベイズ則 　　⇒P(A)P（B|A)=P(B)P（A|B)
　・推測統計：集団から一部（標本）を取り出し元の集団（母集団）の性質を推測する
　　記述統計：集団の性質を要約し記述する
　・期待値：その分布における，確率変数の平均の値 または 「ありえそう」な値 　
　　　離散の場合、
$
　　 　E(f) = \sum_{k=1}^{n}P(X=x_k)f(X=x_k)
　　$
　　 連続の場合、
$
　 　　E(f) = \int_{a}^{b}P(X=x)f(X=x)dx
　　$

・分散と共分散　　
分散
　　　•データの散らばり具合
　 　　•データの各々の値が，期待値 からどれだけズレているのか 平均したもの
　　　　　$　
Var(f)＝E(f^2(X=x))-(E(f))^2
$
　共分散
　　•２つのデータ系列の傾向の違い
　　• 正の値を取れば似た傾向
　　• 負の値を取れば逆の傾向
　　• ゼロを取れば関係性に乏しい
　　　　　$　
Cov(f,g)＝E(fg)-E(f)E(g)
$
　分散と標準偏差
　　　・分散の平方根で計算する。
　　　　　$　
δ＝\sqrt{Var(f)}
$

確率分布
・ベルヌーイ分布 （二項分布 ）、マルチヌーイ（カテゴリカル）分布、ガウス分布 ・・・
・推定量と推定値（真の値を$\theta$とすると…$\hat{\theta}$のように表す
　　推定量(estimator)： パラメータを推定する ために利用する数値の 計算方法や計算式のこ と。推定関数とも。
　　推定値(estimate)： 実際に試行を行った結果 から計算した値

標本平均
　　・サンプル数が大きくなれば、 母集団の値に近づく 　　　　　　　→一致性
　　・サンプル数がいくらであっても、 その期待値は母集団の値と同様 →不偏性

不偏分散
$
S^2＝\frac{1}{n-1}\sum_{i=1}^{n}{(x_i-\hat{x})^2}
$

情報科学情報科学

自己情報量
　　 •対数の底が2のとき，単位はビット(bit)
　　 •対数の底がネイピアのeのとき，単位は(nat)
$
I(x)=-log(P(x))=log（W(x)）
$

シャノンエントロピ
　　 •微分エントロピーともいうが，微分しているわけではない
　　 •自己情報量の期待値

$
H(x)＝E（I(x)）＝－E（log(P(x)))=-\sum(P(x)log(P(x)))
$

機械学習

１、線形回帰モデル
機械学習とは～ハンズオン
・線形回帰▶直線で予測
・非線形回帰▶曲線で予測
式：

 Y=Xw+\epsilon \\
  \qquad x_i=(1,x_{i1},x_{i2},...,x_{im})^T \\
  \qquad Y=(y_1,y_2,...,y_n)^T \\
  \qquad X=(x_1,x_2,...,x_n)^T \\
  \qquad \epsilon=(\epsilon_1,\epsilon_2,...,\epsilon_n)^T \\
  \qquad w=(w_0,w_1,w_2,...,w_m)^T\\

パラメータの推定方法：
・最小二乗法　　⇒平均二乗誤差の最小化
・最尤法　　　　⇒（誤差項$\epsilon_{i}$が互いに独立であることと正規分布に従う）尤度関数の最大化
　　　◆ 回帰の場合には、最尤法による解は最小二乗法の解と一致

非線形回帰モデル
非線形回帰モデル～モデル選択

２、基底展開法
・回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用する
・未知パラメータは線形回帰モデルと同様に最小二乗法や最尤法により推定

$\qquad$・よく使われる基底関数

$\qquad\qquad$
○ 多項式関数 ○ ガウス型基底関数 ○ スプライン関数 / Bスプライン関数
　　　◆基底展開法も線形回帰と同じ枠組みで推定可能
計算式：

$
\qquad y_{i}=w_{0}+\sum_{i=1}^{m}w_{j}\phi_{j}(x_{i})+\epsilon_{i}\
$

・未学習対策
　　　①モデルの表現力が低いため、表現力の高いモデルを利用する
・過学習の対策
　　　①学習データの数を増やす
　　　②不要な基底関数(変数)を削除して表現力を抑止
　　　③正則化法を利用して表現力を抑止

３、ロジスティック回帰モデル
・分類問題を解くための教師あり機械学習モデルである
・ある入力(数値)から確率でクラスに分類する
・確率計算式：
$
　　　P（Y=1|x）＝\sigma(w_{0}+w_{1}x_{1}+…+w_{m}x_{m})
$

・
$
\sigma
$関数の性質：
　　　○ シグモイド関数の微分は、シグモイド関数自身で表現することが可能、尤度関数の微分を行う際にこの性質を利用することで計算が容易になる
・ロジスティック回帰モデルではベルヌーイ分布を利用する
・ロジスティック回帰モデルの最尤推定
　　 ○ 確率pはシグモイド関数となるため、推定するパラメータは重みパラメータとなる
　　 ○ を生成するに至った尤もらしいパラメータを探す
・尤度関数Eを最大化
　　反復学習によりパラメータを逐次的に更新する勾配降下法で解決する
　　データ量が多い場合、確率的勾配降下法を利用する

４、主成分分析
・多変量データの持つ構造をより少数個の指標に圧縮
・情報の量を分散の大きさと捉える
・ 線形変換後の変数の分散が最大となる射影軸を探索
・データの分散共分散行列の固有値と固有ベクトルが、制約付き最適化問題の解となる
・式：
$
　　　Var（\overline{X})＝\lambda a_{j}
$

５、アルゴリズム
k近傍法、
・ 分類問題のための機械学習手法
・最近傍のデータをｋ個取ってきて、それらがもっとも多く所属するクラスに識別
・kを変化させると結果も変わる
・kを大きくすると決定境界は滑らかになる

k近傍法（k-means)
・教師なし学習のクラスタリング手法
・与えられたデータを特徴の似ているもの同士をグループ化する
・中心の初期値を変えるとクラスタリング結果も変わりうる
・kの値を変えるとクラスタリング結果も変わる

６、サポートベクターマシン
・2クラス分類のための機械学習手法
・線形モデルの正負で2値分類する
・線形判別関数ともっとも近いデータ点との距離を（マージン）が最大となる線形判別関数を求める
・式：
　　　　　　
$
y=w^Tx+b=\sum_{j=1}^{m} w_{j}x_{j}+b
$
・線形分離できないとき、誤差を許容し、誤差に対してペナルティを与える
　　　　　　⇒ソフトマージンSVMのパラメータCの大小で決定境界の幅を変更する
・線形分離できない場合、非線形分離を使って特徴空間に写像し、その空間で線形に分離する

線形回帰ハンズオン
■ 考察

ロジスティクス回帰ハンズオン
■ 考察

深層学習（前編１）

Section1：入力層～中間層深層学習1-1～1-6
・入力層から中間層
　　　　⇒①入力層から特徴値が入力されて各入力値に対応する重みを掛ける
　　　　⇒②①にバイアスの値を加える
　　　　⇒③②の結果を中間層の入力として、活性化関数に渡して計算結果を出力する

Section2：活性化関数深層学習1-7～1-8
・活性化関数
　　　⇒ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数。
　　　　　入力値によって、次の層への信号のON/OFFや強弱を定める働きをもつ関数
　　　⇒①ReLU関数 ②シグモイド（ロジスティック）関数 ③ステップ関数
　　　

Section3：出力層深層学習1-9～1-10
・誤差関数
　　　　二乗和誤差クロスエントロピー関数を利用する

・出力層活性化関数
　　　　出力層出力層と中間層で利用される活性化関数が異なる
　　　　　　　⇒①ソフトマックス関数 ②恒等写像 ③シグモイド関数（ロジスティック関数）

Section4：勾配降下法深層学習1-11～1-13
　　深層学習は、学習を通してパラメータを最適化し、出力誤差を最小にするネットワークを作成する目的である。
パラメータを最適化できる勾配降下法は、まさに深層学習のコーアでなる
・勾配降下法
　　　⇒学習率の値によって学習の効率が大きく異なる
•確率的勾配降下法
　　　⇒• データが冗長な場合の計算コストの軽減 • 望まない局所極小解に収束するリスクの軽減 • オンライン学習ができる
•ミニバッチ勾配降下法
　　　⇒ 確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効利用できる

Section5：誤差逆伝播法深層学習1-14～1-18
　　出力誤差を出力層側から順に微分し、前の層前の層へと伝播してパラメータを更新していく。
・最小限の計算で各パラメータでの微分値を解析的に計算する手法
・計算結果（=誤差）から微分を逆算することで、不要な再帰的計算を避けて微分を算出できる

確認テストの考察

【P11】ディープラーニングは、結局何をやろうとしているか2行以内で述べよ。 また、次の中のどの値の最適化が最終目的か。 全て選べ。（1分）
　　　①入力値[ X] ②出力値[ Y] ③重み[W] ④バイアス[b] ⑤総入力[u] ⑥中間層入力[ z] ⑦学習率[ρ]
■ 考察
　　最終目的は②出力値の最適化と思われるが、ディープラーニングにおいては、最適化したパラメータの③重み[W]④バイアス[b]を見つけるのが目的だと考えられる。

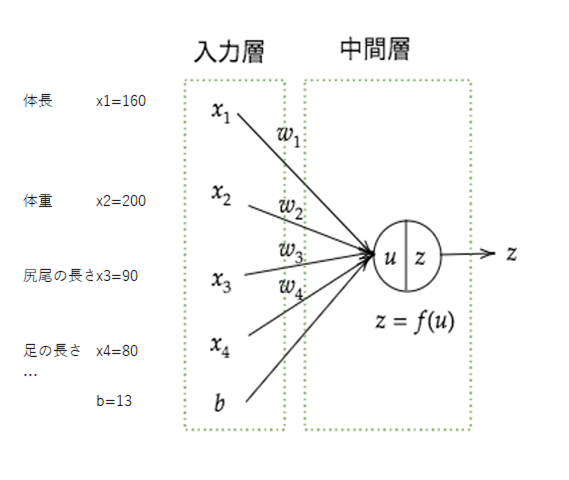
【P13】次のネットワークを紙にかけ。
入力層：2ノード1層
中間層：３ノード2層
出力層：1ノード1層
■ 考察

【P20】確認テスト この図式に動物分類の 実例を入れてみよう。
■ 考察

【P22】次のネットワークを紙にかけ。
$
　　　　　u=w_{1}x_{1}+w_{2}x_{2}+w_{3}x_{3}+w_{4}x_{4}+b\
　　　　　=Wx+b
$
Pythonで書け
■ 考察
　　　　# 重み
　　　　　W = np.array([0.1,0.2,0.3,0.4])
　　　　# バイアス
　　　　　b = 0.5
　　　　# 入力値
　　　　　x = np.array([2,3,4,5])
　　　　　# 総入力
　　　　　u = np.dot(x, W) + b

【P24】確認テスト 1-1のファイルから 中間層の出力を定義しているソースを抜き出せ。
■ 考察
　　　　# 中間層出力
　　　　z = functions.sigmoid(u)

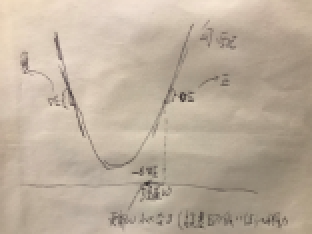
【P27】線形と非線形の違いを図にかいて 簡易に説明せよ。。
■ 考察
　　　　一言といえば、線形は出力が入力と比例関係が成り立っているもの、非線形はそうでないもの

【P34】配布されたソースコードより 該当する箇所を抜き出せ。
■ 考察

# 中間層出力
z = functions.sigmoid(u)
print_vec("中間層出力", z)

【P45】なぜ、引き算でなく二乗するか述べよ ・下式の1/2はどういう意味を持つか述べよ

$
E_{n}(w)=1/2\sum_{j=1}^{J}(y_{j}-d_{j}^2)=1/2||(y-d)||^2\
$
■ 考察
　　　　引き算すると正負の値が、互いにすべて打ち消しあって消えてしまう。
　　　　微分する目的は、元の関数の極小値を求める (導関数が0となる点を求める) ことである。この目的に対して 1/2 を掛ける影響はない。
　　　　 また、微分をした際に「降りてくる」2とこの 1/2 が打ち消しあい 1 となり、計算が簡略化されるため。

【P52】①~③の数式に該当するソースコードを 示し、一行づつ処理の説明をせよ
■ 考察

# ソフトマックス関数
def softmax(x):
    if x.ndim == 2:  
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)  # 分子np.exp(x)：②に該当、分母np.sum(np.exp(x), axis=0) ：③に該当する
        return y.T　　　　　　　　　　　　　　　　# 戻り値：①該当す

    x = x - np.max(x) # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))　　　　　# 戻り値：①該当する、分子np.exp(x)：②に該当、分母np.sum(np.exp(x), axis=0) ：③に該当する

【P54】①~②の数式に該当するソースコードを 示し、一行づつ処理の説明をせよ
■ 考察

# クロスエントロピー
def cross_entropy_error(d, y):
    if y.ndim == 1:
        d = d.reshape(1, d.size)
        y = y.reshape(1, y.size)
        
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    if d.size == y.size:
        d = d.argmax(axis=1)
             
    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size# 戻り値:①に該当　　 -np.sum()：②に該当、

【P57】該当するソースコードを探してみよう。
■ 考察

grad = backward(x, d, z1, y)
network[key]  -= learning_rate * grad[key]

【P66】オンライン学習とは何か 2行でまとめ
■ 考察
　　　データを一つずつ読み込んでその都度モデルの更新を繰り返すことで学習を行う手法である
　　　1回あたりの学習コストが低くデータの変化に対応しやすいなどの特徴がある

【P69】この数式の意味を図に書いて説明せよ
■ 考察
　　　勾配降下法は現在のｗを負の勾配方向(−∇E）に少し動かし、これを何度も繰り返す。

【P79】誤差逆伝播法では不要な再帰的処理を避ける事が出来る。 既に行った計算結果を保持しているソースコードを抽出せよ。

# 誤差逆伝播
def backward(x, d, z1, y):
    print("\n##### 誤差逆伝播開始 #####")

    grad = {}

    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    #  出力層でのデルタ
    delta2 = functions.d_sigmoid_with_loss(d, y)
    #  b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    #  W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    #  中間層でのデルタ
    delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    #  W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
        
    print_vec("偏微分_dE/du2", delta2)
    print_vec("偏微分_dE/du2", delta1)

    print_vec("偏微分_重み1", grad["W1"])
    print_vec("偏微分_重み2", grad["W2"])
    print_vec("偏微分_バイアス1", grad["b1"])
    print_vec("偏微分_バイアス2", grad["b2"])

    return grad
    
# 訓練データ
x = np.array([[1.0, 5.0]])
# 目標出力
d = np.array([[0, 1]])
#  学習率
learning_rate = 0.01
network =  init_network()
y, z1 = forward(network, x)　　　　　　　　　　#network は、既に行った計算結果を保持している

# 誤差
loss = functions.cross_entropy_error(d, y)

grad = backward(x, d, z1, y)
for key in ('W1', 'W2', 'b1', 'b2'):
    network[key]  -= learning_rate * grad[key]  #network[key] は、既に行った計算結果を保持している

print("##### 結果表示 #####")    


print("##### 更新後パラメータ #####") 
print_vec("重み1", network['W1'])
print_vec("重み2", network['W2'])
print_vec("バイアス1", network['b1'])
print_vec("バイアス2", network['b2'])

【P84】2つの空欄に該当するソースコードを探せ
■ 考察
① b2の勾配
　　grad['b2'] = np.sum(delta2, axis=0)
② W2の勾配
　　grad['W2'] = np.dot(z1.T, delta2)