graphillionを使ってみた

はじめに

　まずはフカシギの数え方を見ていただきたい。これは、日本科学未来館で平成24年8月1日(水) ～ 平成25年4月15日(月)の間に公開されていたアルゴリズムの重要性をわかりやすく示した有名な動画である。この動画でわかる通り、アルゴリズムを使うことで計算時間を大幅に短縮することができる。
　そこで、動画内で紹介されていたアルゴリズムをgraphillion（読み方はグラフィリオン）というライブラリを用いてpythonで実際に計算してみる。

graphillionとは

　graphillionとは、グラフ集合を扱うためのライブラリであり、PythonやC++でパスや全域木、マッチングなど、様々な対象を列挙できる。今回は、このグラフ集合ライブラリgraphillionのチュートリアルを実際にpythonで行い、実用性を実感する。

インストール

　まずはgraphillionをインストールする。詳しくはGithubを見てもらいたいが、実際にインストールした手順を示す。なお、環境は MacBook ProのIntel Core i5(64bit)で、Python 3.6.3 である。
　なお、networkxとmatplotlibは必須ではないが、チュートリアルでグラフ図示をする際に必要となる。

pip install networkx
pip install matplotlib
pip install graphillion

　以上のコマンドを打つと、自分のOSとpythonのバージョンに合わせた最適なバージョンがインストールされる。

チュートリアル

　それでは、チュートリアルを行う。

# 必要なモジュールのインポート
from graphillion import GraphSet
import graphillion.tutorial as tl

　まずは、動画でお姉さんが命をかけて挑んでいたグリッドの問題を解く。

# グリッドのサイズを指定
universe = tl.grid(2, 2)
GraphSet.set_universe(universe)
tl.draw(universe)

　この時、tl.draw(universe)で考えているグラフを図示できるので、便利である。今回考えているグリッドは、以下のようになる。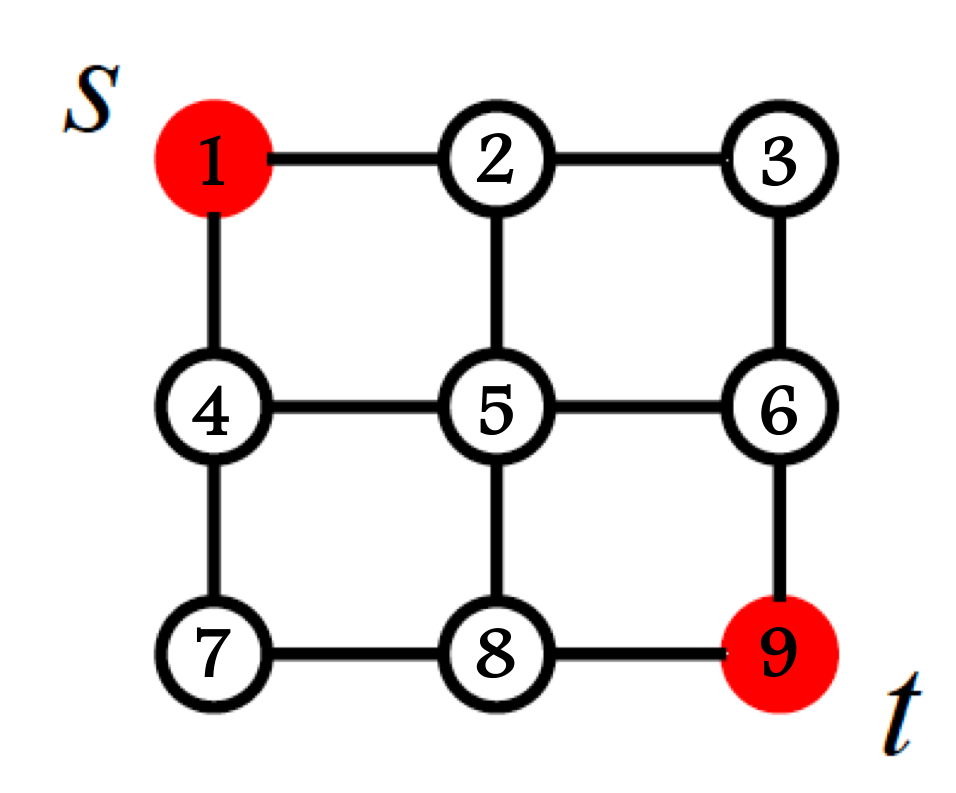

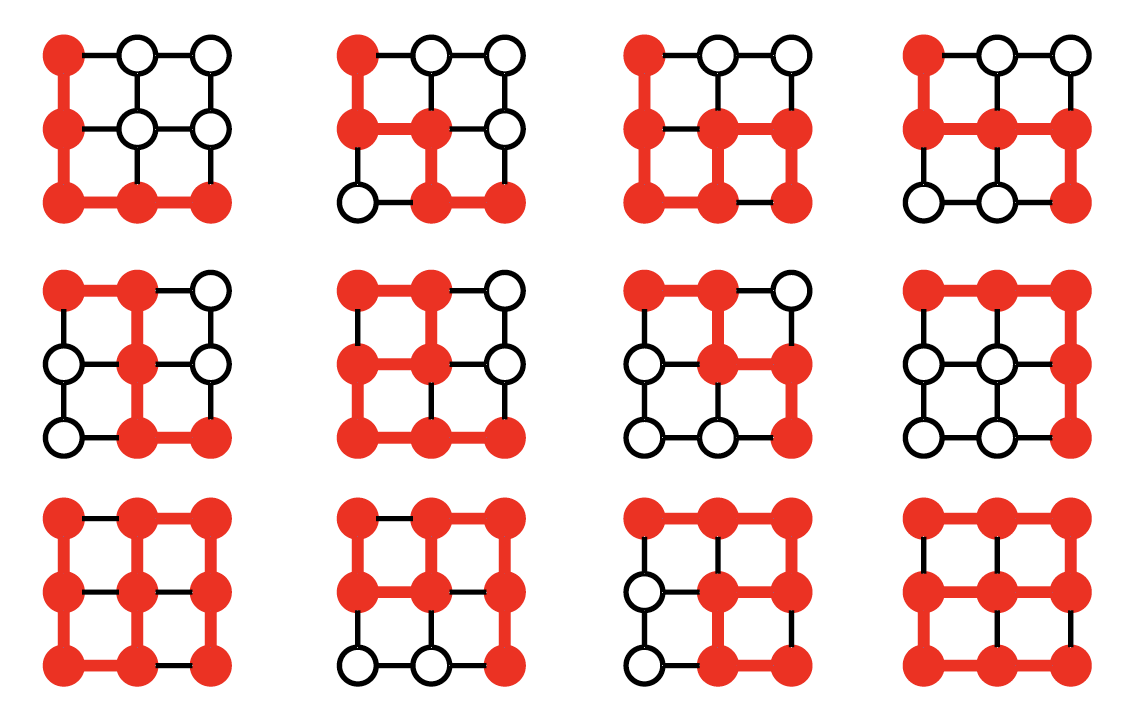
　それでは、実際に経路が何本あるのかを計算する。

start = 1 # スタート位置
goal = 9 # ゴールの位置
paths = GraphSet.paths(start, goal)
len(paths)
>>> 12

　正しい答えも以下の通り12通りである。

　それではここで、この問題の派生問題を解いてみる。「指定された２箇所を指定された順番で通る」という制約付きで道順が何通りあるかを調べる。（チュートリアルでは、"key is picked up before reaching the treasure box" として紹介されている。）

key = 4        # 1箇所目
treasure = 2   # 2箇所目
paths_to_key = GraphSet.paths(start, key).excluding(treasure)
treasure_paths = paths.including(paths_to_key).including(treasure)
len(treasure_paths)
>>> 2

　ここでも正しく計算された。（もちろん選ばれたのは以下の２つ）

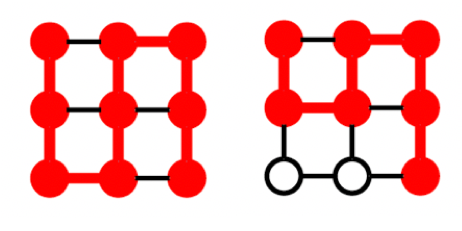
　それでは最後に、お姉さんが６年半もかけてしまった9×9のグリッドで全てのパスを求める時間を調べる。

import time              # 計算時間を調べる。
universe = tl.grid(8, 8) # 9×9のグリッド
GraphSet.set_universe(universe)
start = 1
goal = 81
s = time.time()          # 計算開始時刻
paths = GraphSet.paths(start, goal)
time.time() - s # 計算時間
>>>0.37097..
len(paths)
>>>3266598486981642

　かなり早く計算ができた。

計算時間を短縮できる理由

　端的に言えば、「圧縮と剪定をしているから」である。
　また、graphillionでは、ZDD(Zero-suppressed Binary Decision Diagram) という「集合の集合を表現するデータ構造」を利用している。
　ここで、「１本のパス（道順）」＝「いくつかの辺の集合」と考えることによってパスを集合と捉え、ZDDを利用できる。パスを列挙するアルゴリズムは以下の通り。

1. 辺に順番をつける。（例えば、sから幅優先）
2. 上でつけた順番が早い方から「その辺を通るか通らないか」を決める
3. 等価なパスは圧縮し、不成立が確定しているパスを剪定する

「ZDDを自作して数え上げお姉さんを救ってみた」で、より詳細な解説と自作のZDDアルゴリズムを紹介しているので、興味がある人は見て欲しい。

参考文献

フロンティア法 - 組合せ問題の解を列挙 索引化するZDD構築アルゴリズム
(北海道大学 情報科学研究科 川原純助教のスライド)