剰余の無い言語で剰余を作る

　この記事を読んではじめてゲームプログラミング(はじプロ)に興味を持ち、更に遊んでくれる人が増えたら嬉しいな！という意図の紹介記事です。このゲームのコアなプレイヤーがどんな遊び方をしてるか伝われば幸いです。

問題

　以下のリファレンス(ノードン機能一覧)に登場するノードン¹を用いて、与えられた整数 X を定数(7)で割った余りを求める回路を作りなさい。但し、はじプロで扱える数値は浮動小数点型のみであり、整数型は利用できません。例えば4÷3を実行すると小数点以下の値を持つ数値(1.333333...)になります。

---

　剰余演算子は汎用的に使える事が望ましいですがゲームに使用することを前提に置くと、除数は固定値(プログラム中のハードコード)であっても問題ないケースが多い印象です。実用的な解を求めている為、この問題は汎用的な剰余回路ではなく定数(7)で剰余を求める事としました。

リファレンス

リファレンスの抜粋

　基本的には中間ノードン²を利用しますが、別解もありえるので³全てのノードンを利用可能とします。
　数値計算に関する中間ノードンには以下の種類があります。さらっと記事だけ読みたい人向けにヒントになる個所を強調しています。

中間ノードン名	コスト	機能概要
計算	1	二つの入力値に対して＋－×÷を行う。
マッピング	1	入力範囲n～mを出力範囲o～pに変換する。任意のa,bを用いたaX+bの１次式と同じ。
デジタル化	1	入力された値を近傍の整数に変換する。四捨五入。
ルート	1	入力値の平方根を求める。sqrt()
絶対値	1	入力値の絶対値を求める。abs()
±反転	1	符号を反転する。
0から変わった瞬間	16	入力が0から0以外に変わった時、1/60秒(1フレーム)だけ1を出力する。
位置を角度に	1	入力座標(x,y)に対して原点(0,0)からの角度Θを求める。arctan()
角度を位置に	1	入力角度Θに対して半径1の円上のx,yを求める。sin(), cos()
角度の差	1	二つの入力角度Θ1,Θ2を比べて近いほうの角度(内角)を求める。±180を超える角度が入力された場合でも、出力は±180度以内に変換される。
くらべる	1	二つの入力値に対し=,>,<,≧,≦の比較を行い、真なら1を出力する。
AND	1	二つの入力値が共に0でない場合、1を出力する。
NOT	1	一つの入力値が0の場合1, 0以外の場合0を出力する。
フラグ	16	0以外の入力があった場合フラグが立ち、以降1を出力し続ける。
カウンター	16	入力された値を1/60秒(1フレーム)毎に加算または減算し続ける。無制限、範囲指定、ループ、往復のモードがある。

　表中のコストは１秒を960分割した時、その処理を完了するのに必要な時間です。16とあるのは960÷16=60、つまり60fpsの１フレームに相当し、1とあるのは60fpsの1/16フレームに相当します。はじプロ自体は60fpsで動作するのでそれより短い時間内に計算が完了していれば、次回画面表示のサイクルに間に合います。
　ノードン数が少なければより多くの実装が期待できますし、コストが1フレームより短かければ快適なゲーム体験になります。よって少ないノードン数・少ない計算時間がより優れた回路になります。

背景説明

　すぐに解答をかいてしまうと記事として面白くないでしょうから背景説明を少々。

剰余は便利

　今どきのプログラミング言語にはほぼ確実に言語機能として用意されている剰余(%)演算が、はじプロには用意されていません⁴。とても便利な演算ですが、これが無いと色々と凝った事が出来ません。Qiitaの中を剰余で検索すると役に立つ記事が沢山ありますので、是非検索してみてください。

剰余のユースケース

　ゲームを作るゲームなのでゲームへの適用を考えると、偶数奇数を求める半丁賭博・疑似乱数を生成する線形合同法(モンスターハンターのお守りテーブル)、ゲーム以外でも公開鍵/秘密鍵による暗号化といった様々な用途に剰余が使われています。

はじプロのリソース制限

　1ファィル内に配置出来るノードン数は512個まで、の制限があります。Unityで例えると「GameObject1つ」「C#のコード1行」「Materialにアタッチする画像1枚」「Audio Sourceにアタッチする音源1つ」がほぼ1ノードンに相当します。
　この制限が厳しくちょっと気の利いた事をやるとあっという間にノードン制限に引っ掛かり、最初の頃は泣く泣く実装を諦める事がとても多いのです。
　最近ではこの制限の中でどれだけ気の利いたことを実装しきれるか、を楽しむパズルをやってる感覚になってきています。

ショートコーダーの愉しみ

　ゲームを作るゲームなので色々なフィーチャーを実装したい。でもリソース制限がキツイ。こんな時どうするか？同じ結果を出力するより少ないノードン数での回路設計が必要になります。
　かくして一部のコアプレイヤーはショートコードの開発に没頭します。得られた成果はコミュニティへ報告し⁵、皆が快適なゲーム制作が出来るよう今でも探求は続いています。

解答

　以下の実装例は 13 % 7 = 6 を例に解説しています。

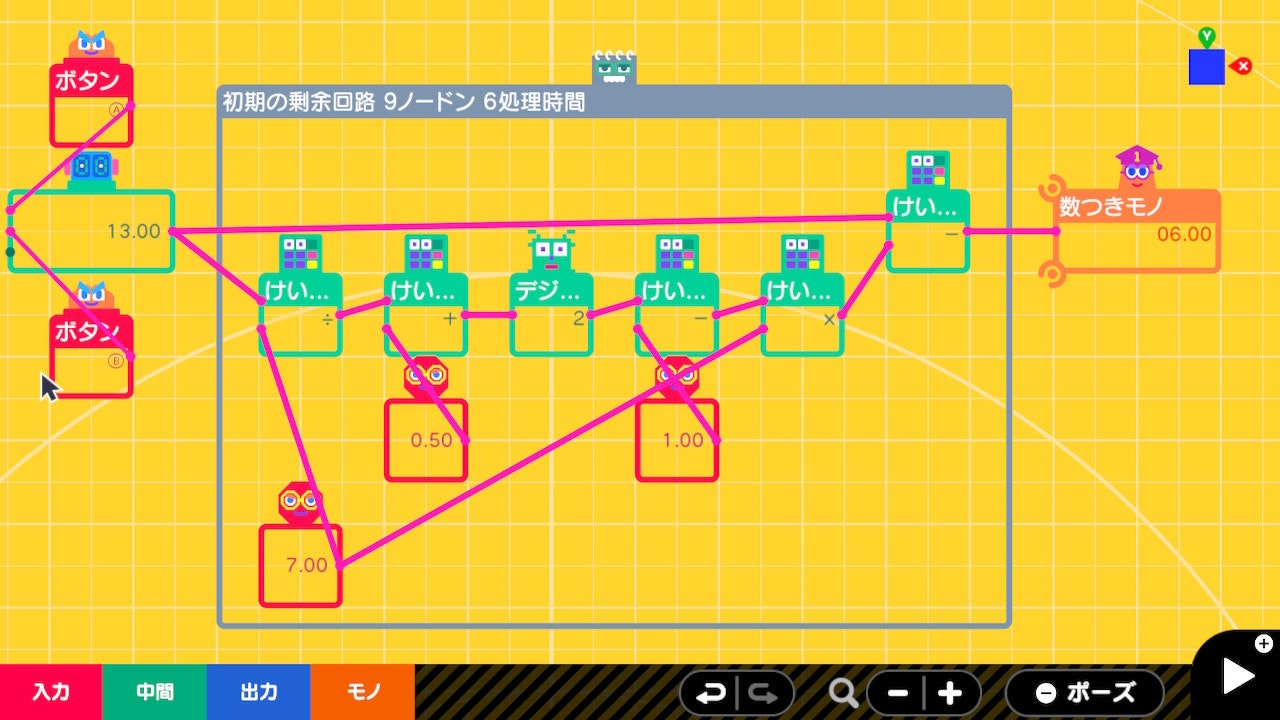
初期の剰余回路

　単純に剰余を求める回路内に定数(7)をハードコードした実装例です。定数部分を外に出せば汎用的な剰余回路になります。まだノードンの特性が良く分かっていない頃の実装例ですが、剰余を求める例として理解しやすいでしょう。

1. 13 ÷ 7 を求める(= 1.8571....)
2. 0.5を足す(= 2.3571...)
3. 四捨五入する(= 2.0)
4. 1を引く(= 1.0) ※13÷7の商(1)が得られる
5. 先に求めた商(1)と除数(7)をかける
6. 被除数(13)から商(1)と除数(7)をかけた数を引く

　高々剰余を求めるだけで9ノードン消費するのはちょっと贅沢過ぎて安直に採用するのは躊躇します。この後マッピングを用いて1つのノードンにX+0.5やX-1の定数をカプセル化する手法が見つかりましたが、ここでは割愛します。

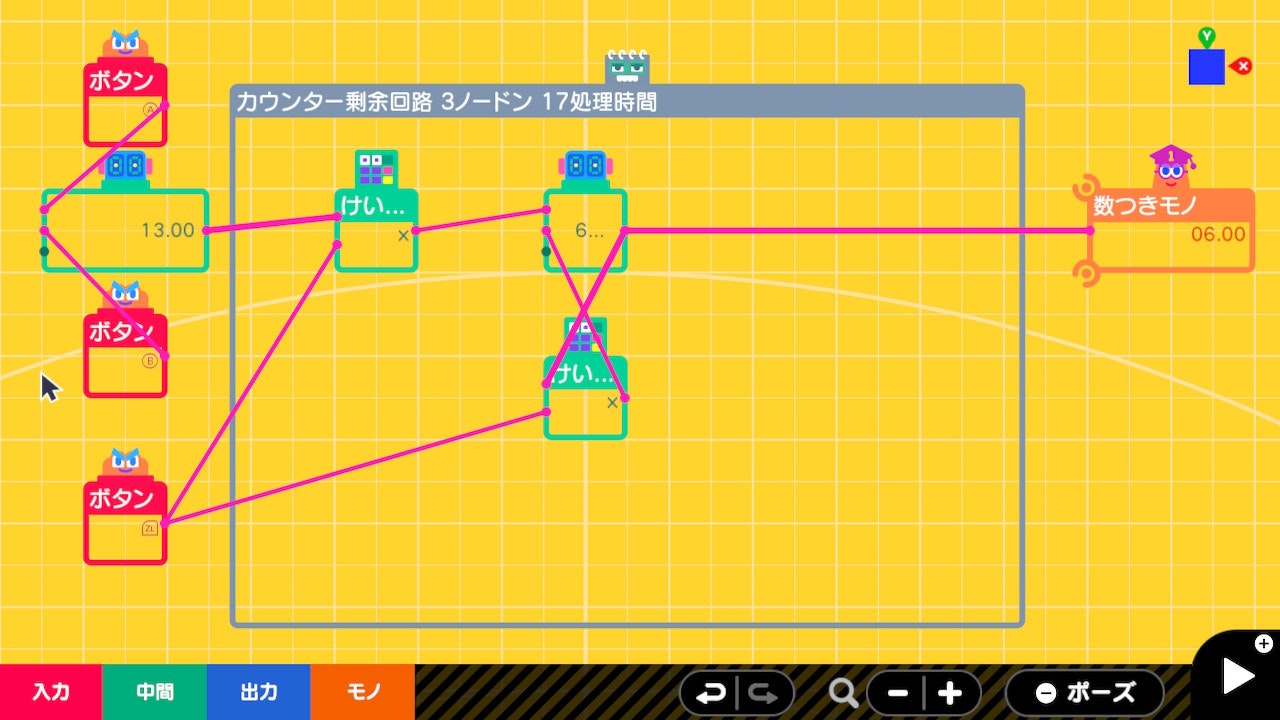
ノードン数の少ない剰余回路

　カウンターのモードをループに設定し、入力した数が上限値を超えていた場合、その剰余がカウンター内に保持される性質が見つかった事で一気に剰余が使いやすくなりました。剰余演算自体はカウンターノードン単体で実現できる事が発見されたわけです。
　カウンターノードンの入力は毎フレーム加算され続ける性質を持つので、この実装例では条件をそろえる為にZLボタンを押した時だけカウンターの現在値を減算し、かつ入力値を受け取るようにしてあります。
　カウンターを通過するのに1フレームを要する為、普通の人は気が付かない程度の計算遅延を受け入れる必要がありますが、実質1ノードンで剰余が計算できるのはとても強力な前進でした。

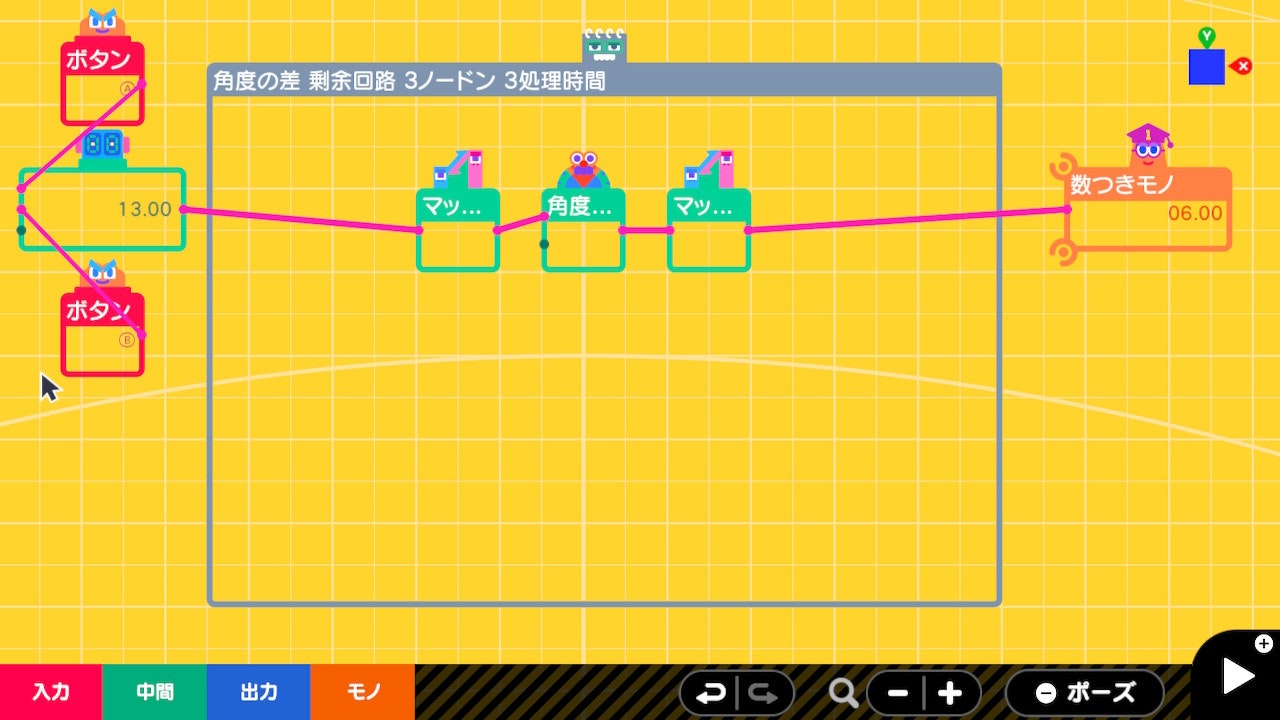
高速な剰余回路

　角度の差に入力された値が範囲外の場合±180度⁶の該当角度に変換される事を利用した剰余回路です。
マッピング1は input(0～7)をoutput(-180～180)に変換
角度の差は差を取る対象が0なので単に入力値を±180の範囲内に変換
マッピング2は input(-180～180)をoutput(0～7)に変換します。

簡単の為、360度を7等分した約51度刻みで表に示ます。
表の数値は各ノードンの変換結果である出力値を表します。

入力値	マッピング1	角度の差	マッピング2	備考
0	-180	-180	0
1	-129	-129	1
2	-78	-78	2
3	-27	-27	3
4	24	24	4
5	75	75	5
6	126	126	6
7	180	-180	0	一周して180→-180に変換
8	231	-129	1
9	282	-78	2
10	333	-27	3
11	384	24	4
12	435	75	5
13	486	126	6
14	540	-180	0	180+360=540

360の約数でない除数の場合、厳密には計算誤差が生じており5.9999...が出力されますが、毎フレーム毎に再計算される状況であれば目立つ問題とはならないでしょう⁷。
リアルタイムなゲームへの適用であれば問題なく動作する回路です。

おわりに

ゲーム制作を目的にするとリソース制限が厳しいミニマムなゲームエンジンですが、数学パズルやこの手の探求が好きな人なら別の愉しみ方が出来るゲームです。
興味を持った方、ぜひ一緒にハック遊びましょう。

1. 入力、計算、出力等の機能を持つコンポーネント。左右に入出力端子を持ちワイヤーで他のノードンと結線することで数値を伝搬します。 ↩

2. ノードンは入力、中間、出力、モノ(画面内に描画されるオブジェクト)に大別されます。　 ↩

3. はじプロの格言に「数学でダメなら物理で殴れ」というのがあります。 ↩

4. 次回作があれば実装してほしい機能の筆頭です。 ↩

5. twitterでハッシュタグを付けてツイートするだけですが、有益そうな内容は私が収集・記録・公開しています。 ↩

6. +180度は-180度と等しい為、厳密には-180≦Θ<180の範囲に変換されます。 ↩

7. 試しにこの回路から出力される値を加算し続けたとしても、220秒経過(220×60=13200回加算)するまで小数点以下第二位に計算誤差が生じません。 ↩