はじめに
本記事では,研究の一環としてESP-WROOM-32(ESP32)という機器を用いBLE を使った屋内測位を行ったとき,RSSI を用い座標変換をしたので,TxPowerを用いた距離変換,計算手法の説明および実装方法について説明する.
三点測位(座標の求め方)
TxPowerとRSSI値を用いた距離変換
送信機の放出する電波が全方位に均等に放出される場合,電力P($mW$)は距離$D$($m$)を半径とする球の表面積$S$に広がり,式$(1)$と表せる.
$S = 4 \pi D^2$...$(1)$
単位面積あたりの電力=電力密度を$P_D$($mW$/$m^2$)とすると,電力密度$P_D$は電力$P$を,通信距離$D$を半径とした球の表面積,式$(1)$で割った値になり,式$(2)$で表せる.
$P_D = \frac{P}{S}$...$(2)$
式$(1)$,$(2)$から電波は「距離の2乗に比例して減衰する」ということになる.
電力の単位は,通常$W$(ワット)だが,通信に使用する比較的小さい電力の表示は$dBm$を使用される.これは1$mW$を基準として対数表示したものであり,$dB$の後ろに$mW$の$m$を付加する.
よって,RSSIは対数で受信電力$P_D$の大きさを表し,RSSIとTxPowerを用いての式に変換すると式$(3)$となる.
$RSSI = 10\log_{10}\frac{P}{S}$
$= 10\log_{10}\frac{P}{4\pi} - 10\log_{10}D^2$...$(3)$
送信機からの距離100(cm)でのRSSIの値をTxPowerとするとき,式$(3)$で$D=1$とすると,式$(4)$が得られ、式$(4)$から式$(5)$を得ることができる.
$TxPower = 10\log_{10}\frac{P}{4\pi}$
$RSSI = TxPower - 10\log_{10}D^2 = TxPower - 20\log_{10}D$...$(5)$
式$(5)$の20という定数は論理値であり,実際には場所により異なる値となることが知られている.定数20をRSSI減衰定数Nとし,それぞれの場所に適した値にする必要がある.
式$(5)$を減衰定数$N$とし,式$(6)$に変形することにより距離$D$が求めることが可能になる.
$D = 10^\frac{TxPower - RSSI}{N}$...(6)
- $D$:距離(cm)
- $RSSI$:計測したRSSI値(dBm)
- $TxPower$:100$cm$での$RSSI$値
- $N$:$RSSI$の減衰定数(理論値:20)
※RSSI と TxPower からビーコンとの距離および近接度(Proximity)を推定する(https://qiita.com/shu223/items/7c4e87c47eca65724305)
# RSSI値から距離変換
def RSSItoMetricConversion(rssi):
TxPower = # 100cmでのRSSI値(受信信号強度)
n = # n = 2.0 : 障害物のない理想空間, n < 2.0 : 電波が反射しながら伝搬する空間, n > 2.0 : 障害物に吸収され減衰しながら伝搬する空間
distance = 10 ** ((TxPower - rssi) / (10 * n))
return round(distance, 2)
# RSSI値代入
rssi_a = 計測したRSSI値(A)
rssi_b = 計測したRSSI値(B)
rssi_c = 計測したRSSI値(C)
# 距離変換呼び出し
distance_a = RSSItoMetricConversion(rssi_a)
distance_b = RSSItoMetricConversion(rssi_b)
distance_c = RSSItoMetricConversion(rssi_c)
計算手法
送信機の放出する電波が全方位に均等に放出される場合,RSSI値から得られる距離$D$を半径$r$とする球の中心から,球面(球の表面)上のどの点までも,その距離$D$は一定=半径$r$となる.
下図,中心点Cから球面までの距離を$r$とすると,PC間の距離は常に等しい.
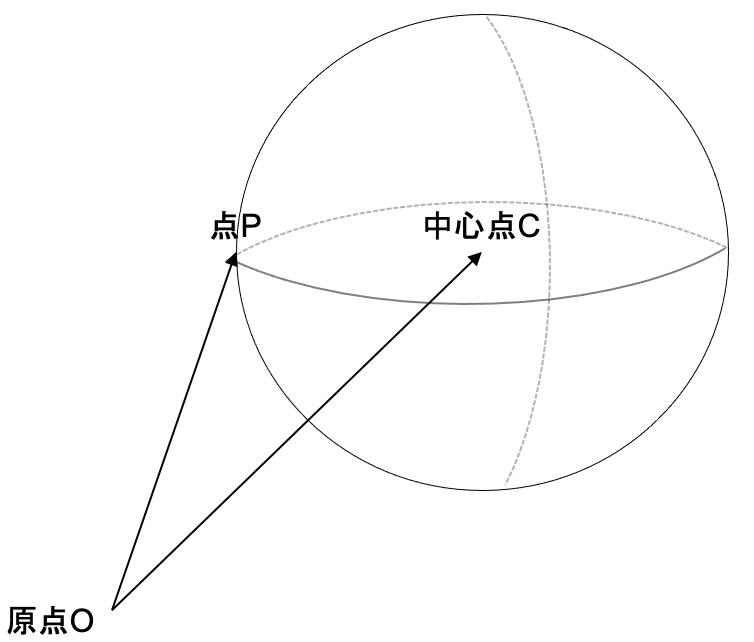
そこで,球面上の点Pと中心点Cの位置ベクトルを使って,球面のベクトル方程式を式$(1)$のように表すことができ,さらに点Pの座標$(x,y,z)$,点Cの座標をC:$(c_x,c_y,c_z)$とすると,式$(2)$を表すことができる.
$ \left| \vec{p} - \vec{c} \right| = r$...$(1)$
$\left| x-c_x, y-c_y, z-c_z \right| = r$...$(2)$
また,式$(2)$の両辺を2乗すると絶対値が外れ,球面の方程式$(3)$を導くことができる.
$(x - c_x)^2 + (y - c_y)^2 + (z - c_z)^2 = r^2$...$(3)$
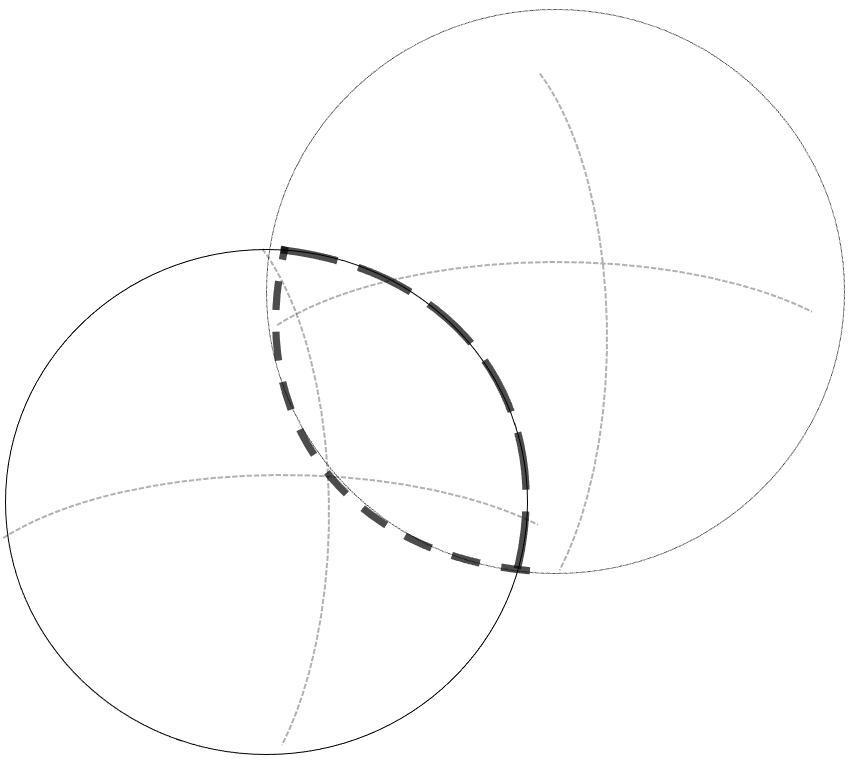
上図では,空間座標中に球体が2つ存在し,それらが交わるとき,その交わった面は円となることを示し,以下では各球からなる交線上にある共有座標の算出について説明する.
点Aを中心とする球の座標をA:$(a_x, a_y, a_z)$,半径$r_A$をとし,点Bを中心とする球の座標をB:$(b_x, b_y, b_z)$,半径$r_B$とする.このとき式$(3)$で導いた球面の方程式にA,B座標を代入することにより式$(4)$,$(5)$が得られる.
$(x - a_x)^2 + (y - a_y)^2 + (z - a_z)^2 = r_A^2$...$(4)$
$(x - b_x)^2 + (y - b_y)^2 + (z - b_z)^2 = r_B^2$...$(5)$
式$(4)$,$(5)$で得られた点A,Bを中心とした球体の方程式を連立方程式として解くことにより,2つの球体からなる交線の方程式となり,式$(6)$のように表せる.
$(2a_x - 2b_x)x + (2a_y - 2b_y)y + (2a_z - 2b_z)z$
$= r_b^2 - r_a^2 + (a_x^2 + a_y^2 + a_z^2) - (b_x^2 + b_y^2 + b_z^2)$...$(6)$
座標変換を行う際は上記の流れ,式に従い計算を行い,全ての方程式を同時に成り立たせる未知数(x,y,z)の値を連立方程式の解とし,座標変換を行う.
import sympy
x, y, z = sympy.symbols("x, y, z")
# 送信機座標
ax, ay, az = 0.0, 0.0, 0.0
bx, by, bz = 0.0, 2.0, 0.0
cx, cy, cz = 2.0, 2.0, 0.0
def AB(ax , ay, az, bx, by, bz, distance_a, distance_b):
AB_left = 2*(ax - bx)*x + 2*(ay - by)*y + 2*(az - bz)*z
AB_right = distance_b**2 - distance_a**2 + (ax**2 + ay**2 + az**2) - (bx**2 + by**2 + bz**2)
AB_y = round(AB_right / (AB_left / y),1)
return AB_y
def AC(ax, az, cx, cz, distance_a, distance_c):
AC_left = 2*(ax - cx)*x + 2*(az - cz)*z
AC_right = distance_c**2 - distance_a**2 + (ax**2 + az**2) - (cx**2 + cz**2)
AC_x = round(AC_right / (AC_left / x),1)
return AC_x
def ABC(ax, ay, az, ABC_x, ABC_y, distance_a):
ABC_left = z**2 - 2*az*z
ABC_right = distance_a**2 - (ABC_x - ax)**2 - (ABC_y - ay)**2 - az**2
ABC_func = sympy.solve(ABC_left + ABC_right)
return round(ABC_func[1],1)
# ABC
ABC_y = AB(ax , ay, az, bx, by, bz, distance_a, distance_b)
ABC_x = AC(ax, az, cx, cz, distance_a, distance_c)
ABC_z = ABC(ax, ay, az, ABC_x, ABC_y, distance_a)
print(f"ABC(x, y, z) = {ABC_x, ABC_y, ABC_z}")
終わりに
3次元での3点測位を行った座標計算方法を紹介した.
計算手法でのプログラムに関し座標に応じ変更する必要があり,改善の余地がある.
また,電波が球状に広がるのはあくまで仮定であり,2.4GHz帯の電波はWifや他の電波から干渉を受けやすく,誤差が出やすいことから座標計算を行う上でも誤差が生じてしまう.
であることから,何らかの工夫を用いることによりRSSI値からより正確な距離に変換する必要があると考える.