昨日の記事でも星形を描きましたが、あれは正確には五芒星です。
今回描きたいのは、中が空っぽな星形(☆)です。
「五光星」とか「五稜星」とか言うんですかね?(要出典)
昔、博士コース時代の研究で星形の10頂点が必要だったので導出しました。
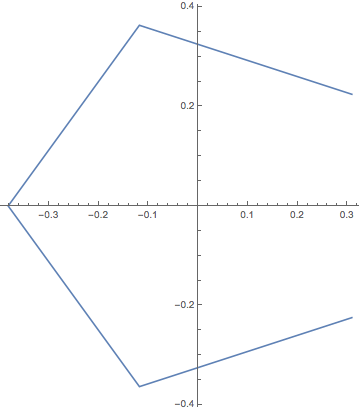
(-1)^Range[0, 4, 4/5]
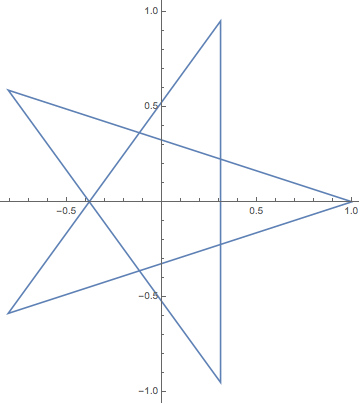
ListPlot[{Re[#], Im[#]} & /@ %, Joined -> True, AspectRatio -> Automatic]
これが昨日書いた五芒星です。
中の抜けた星形にするには輪郭をなぞるように描けばいいのですが、そのためには5つの交点の座標を求める必要があります。
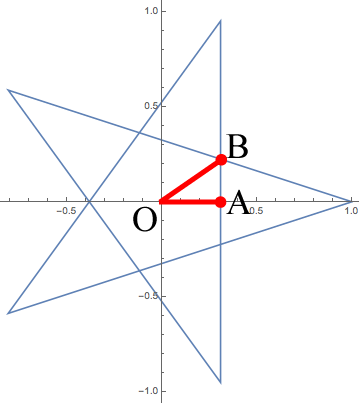
以下の図を用いて求め方を軽く説明します。
三角形OABは直角二等辺三角形です。
この3角形は正5角形の$\frac1{10}$ピースなので、
$\angle BOA = 36^\circ$
となります。
また、点$A$は点$B$の$x$軸での射影のため、
$|OA| = |OB| \cos(36^\circ)$
となります。
よって
$|OB| = \frac{|OA|}{\cos(36^\circ)}$ (式1)
となります。
点$A$は最初の正5角形の3番目および4番目の点と同じ$x$座標なので、
Re[(-1)^Range[0, 4, 4/5]][[3]]
→ $\frac{\sqrt5 - 1}4$
となります。
(式1)に代入して、
1/Cos[Pi/5]*(Sqrt[5] - 1)/4 // FullSimplify
→ $\frac{3 - \sqrt5}2$
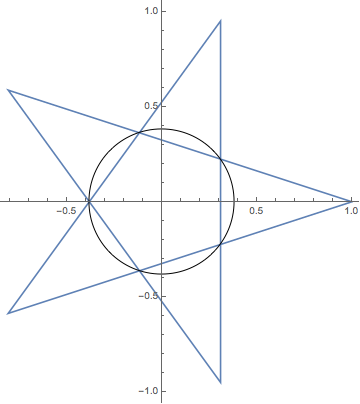
が小さい5角形の外接円の半径となります。
プロットするとぴったり合いますね。
(-1)^Range[0, 4, 4/5];
Show[
ListPlot[{Re[#], Im[#]} & /@ %, Joined -> True, AspectRatio -> Automatic],
Graphics[Circle[{0, 0}, (3 - Sqrt[5])/2]]
]
外側の5角形は
(-1)^((2 Range[0, 8, 2])/10)
ListPlot[{Re[#], Im[#]} & /@ %, Joined -> True,
AspectRatio -> Automatic]
内側の5角形は
(3 - Sqrt[5])/2 (-1)^((2 Range[1, 10, 2])/10);
ListPlot[{Re[#], Im[#]} & /@ %, Joined -> True,
AspectRatio -> Automatic]
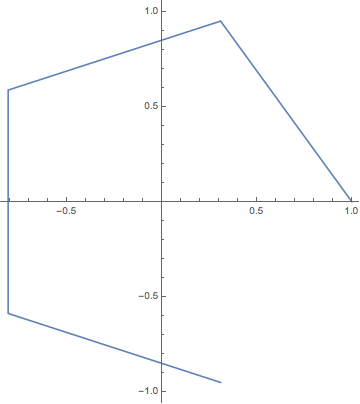
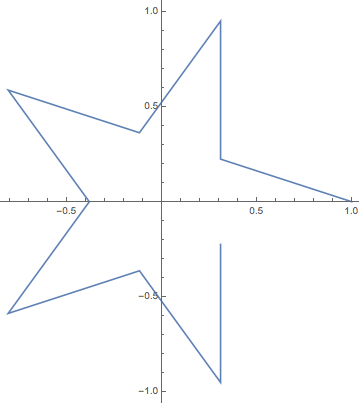
交互になぞれば
Riffle[
(-1)^((2 Range[0, 8, 2])/10),
(3 - Sqrt[5])/2 (-1)^((2 Range[1, 10, 2])/10)
];
ListPlot[{Re[#], Im[#]} & /@ %, Joined -> True, AspectRatio -> Automatic]
これを$xy$軸逆転して、Graphicsで星っぽく描画します。
Graphics[{EdgeForm[Thick], Yellow,
Polygon[{Im[#], Re[#]} & /@ Riffle[
(-1)^((2 Range[0, 8, 2])/10),
(3 - Sqrt[5])/2 (-1)^((2 Range[1, 10, 2])/10)
]]
}]
完成です!
今日知った関数ですが、新機能 RegionUnion で同じようなことができるかもしれません。