複素数を余裕でサポートしているMathematicaは、2Dグラフィックスをより簡単に処理できます。
座標としてリストを用いた星形の描画
例として星形を使います。
星形を描くには次のように組むとある程度すっきりするでしょう。
listPts = Table[{Cos[a Pi], Sin[a Pi]}, {a, 0, 4, 4/5}]
ListLinePlot[listPts, AspectRatio -> Automatic]
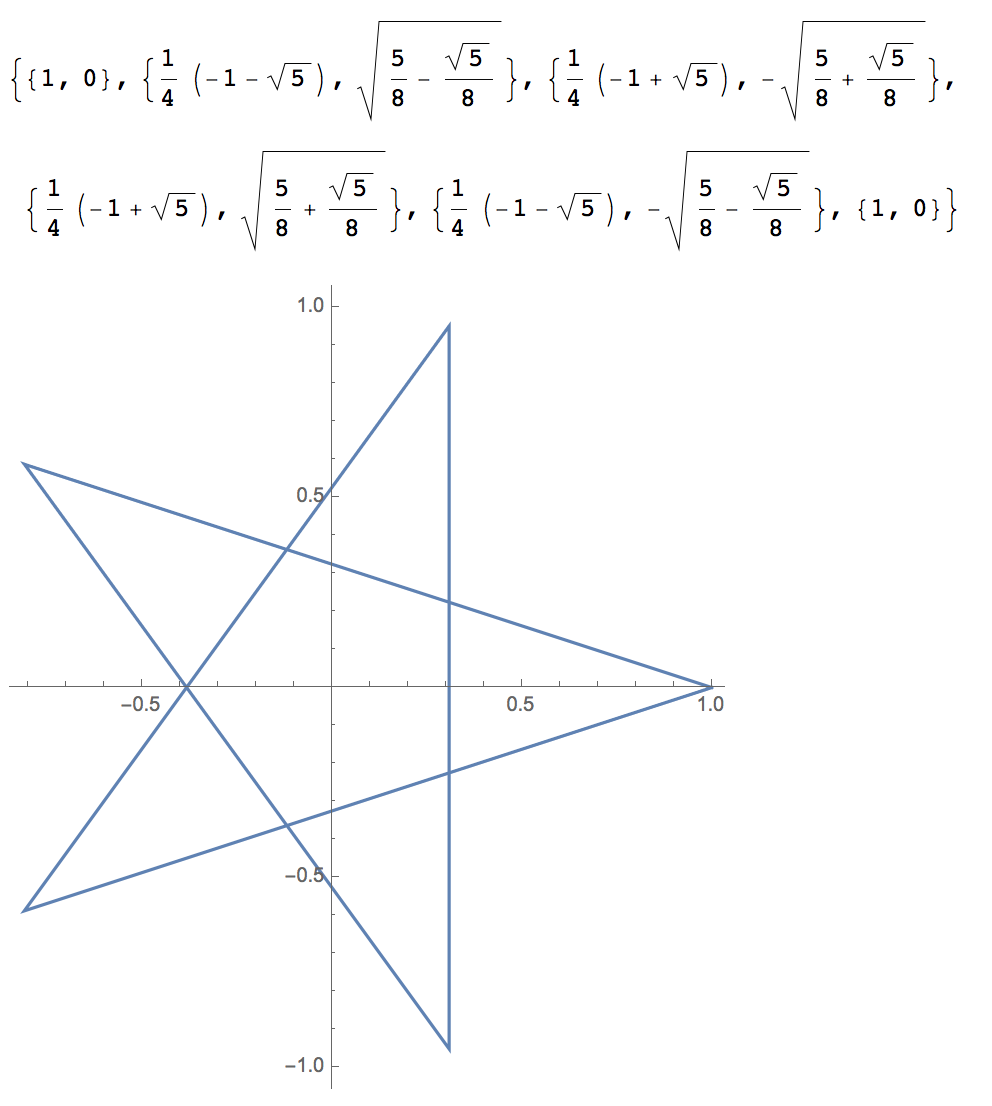
平行移動
これを右に1、上に2だけ平行移動するには、以下のように座標 $(1, 2)$ を足せばいいでしょう。
listPtsに直接{1, 2}を足すのも直感的に行けそうな気がするかもしれませんが、次元が合わないのが駄目なようなのでやむなくリストのそれぞれに適用させます。
listPts2 = (# + {1, 2}) & /@ listPts
ListLinePlot[listPts2, AspectRatio -> Automatic]
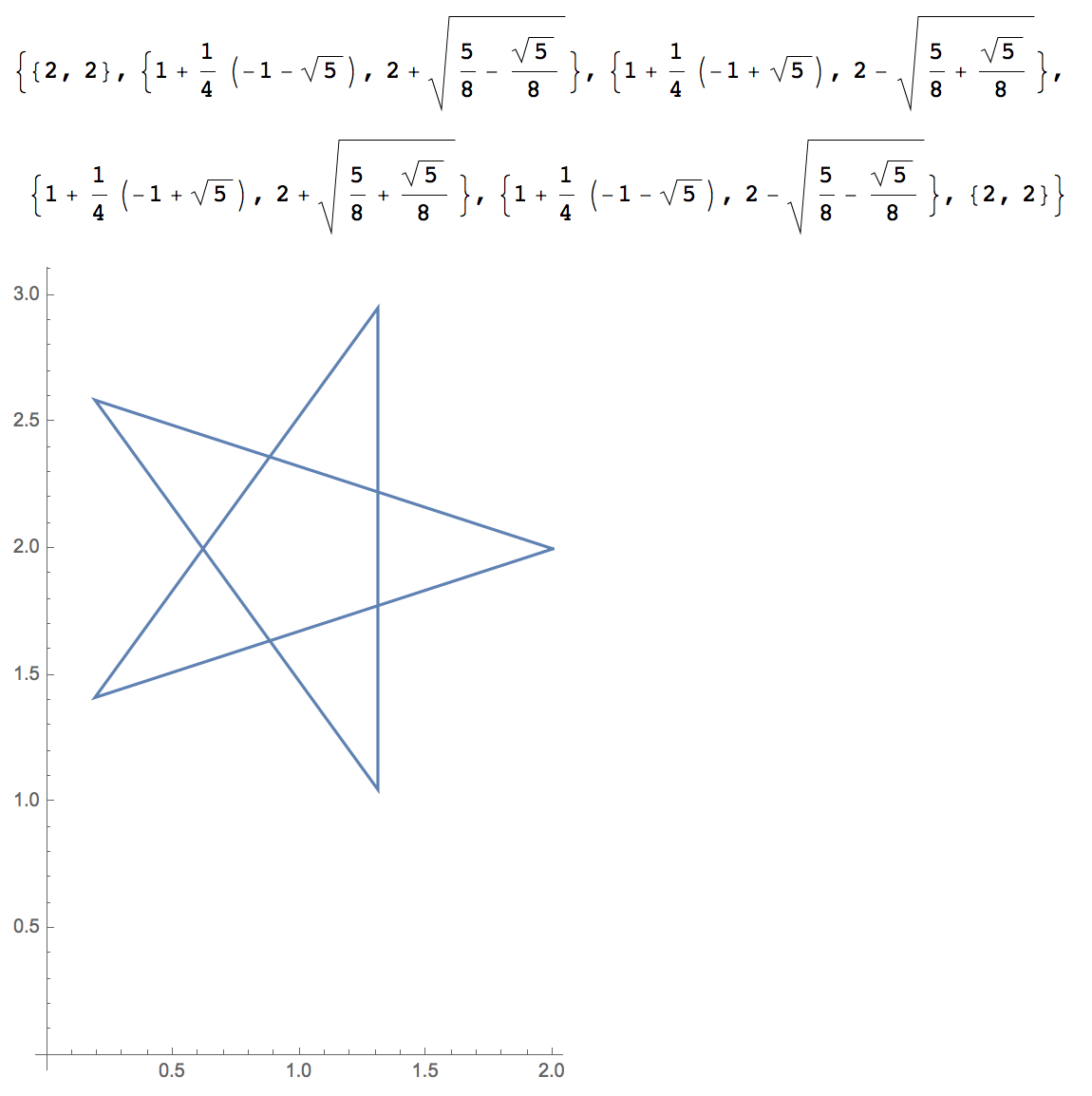
回転
ベクトル解析をやったことのある人はわかると思いますが、
ベクトルをアフィン変換(回転、拡大縮小など)するには行列を掛ける必要があります。
Mathematicaには回転行列などを求める関数があるので比較的楽に行えます。
listPts2 = (RotationMatrix[30 Degree].#) & /@ listPts
ListLinePlot[listPts2, AspectRatio -> Automatic]
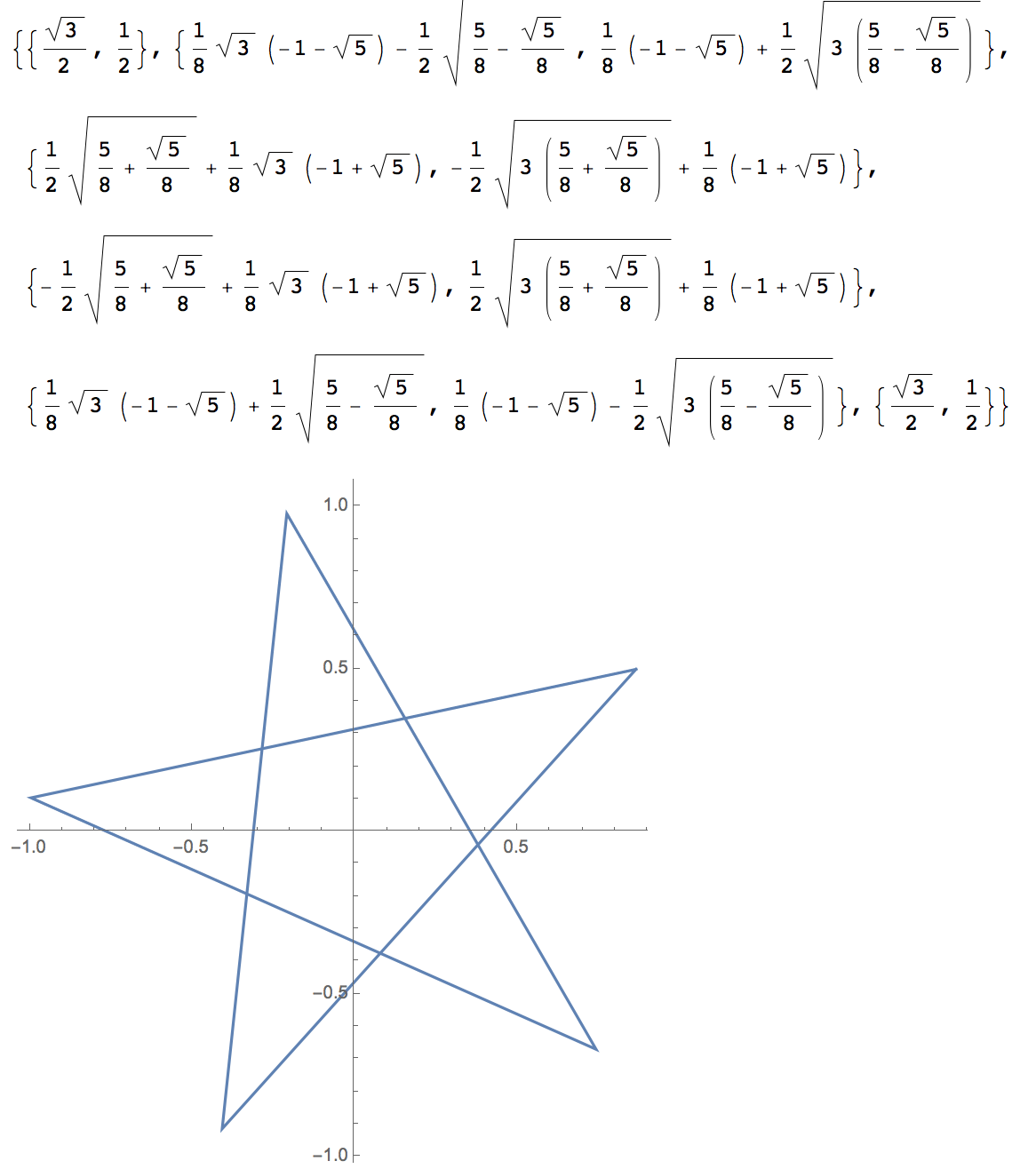
が、これもちょっと面倒だと(僕は)思います。
座標として複素平面を用いた星形の描画
複素平面上の複素数として座標値を扱うと、魔法のように扱いやすくなります。
compPts = (-1)^Range[0, 4, 4/5]
{Re[#], Im[#]} & /@ compPts
ListLinePlot[{Re[#], Im[#]} & /@ compPts, AspectRatio -> Automatic]
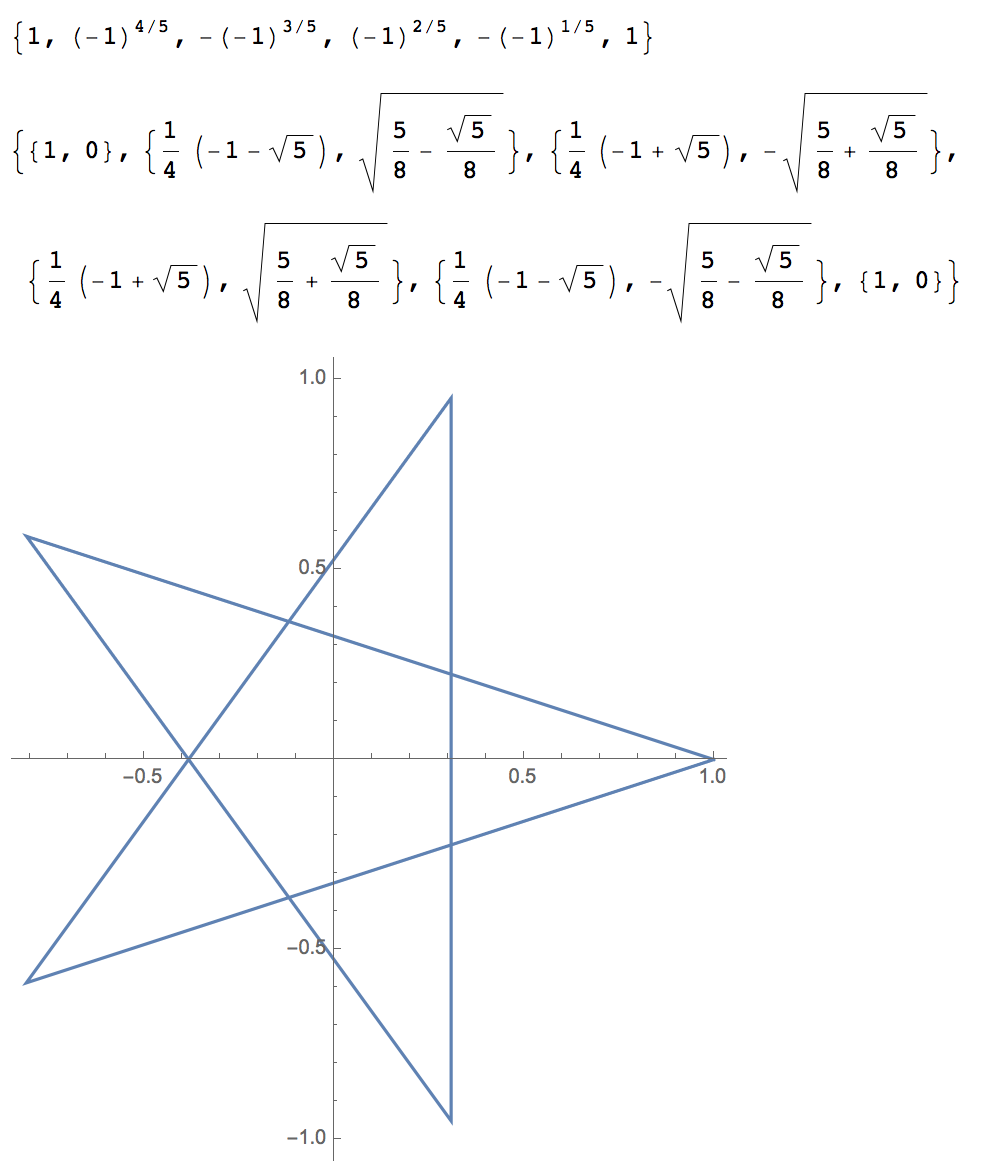
{Re[#], Im[#]} & /@ compPtsが先ほどのlistPtsに相当します。
でも、まだ有り難みが感じられませんね。
では、以下の場合はどうでしょう。
平行移動
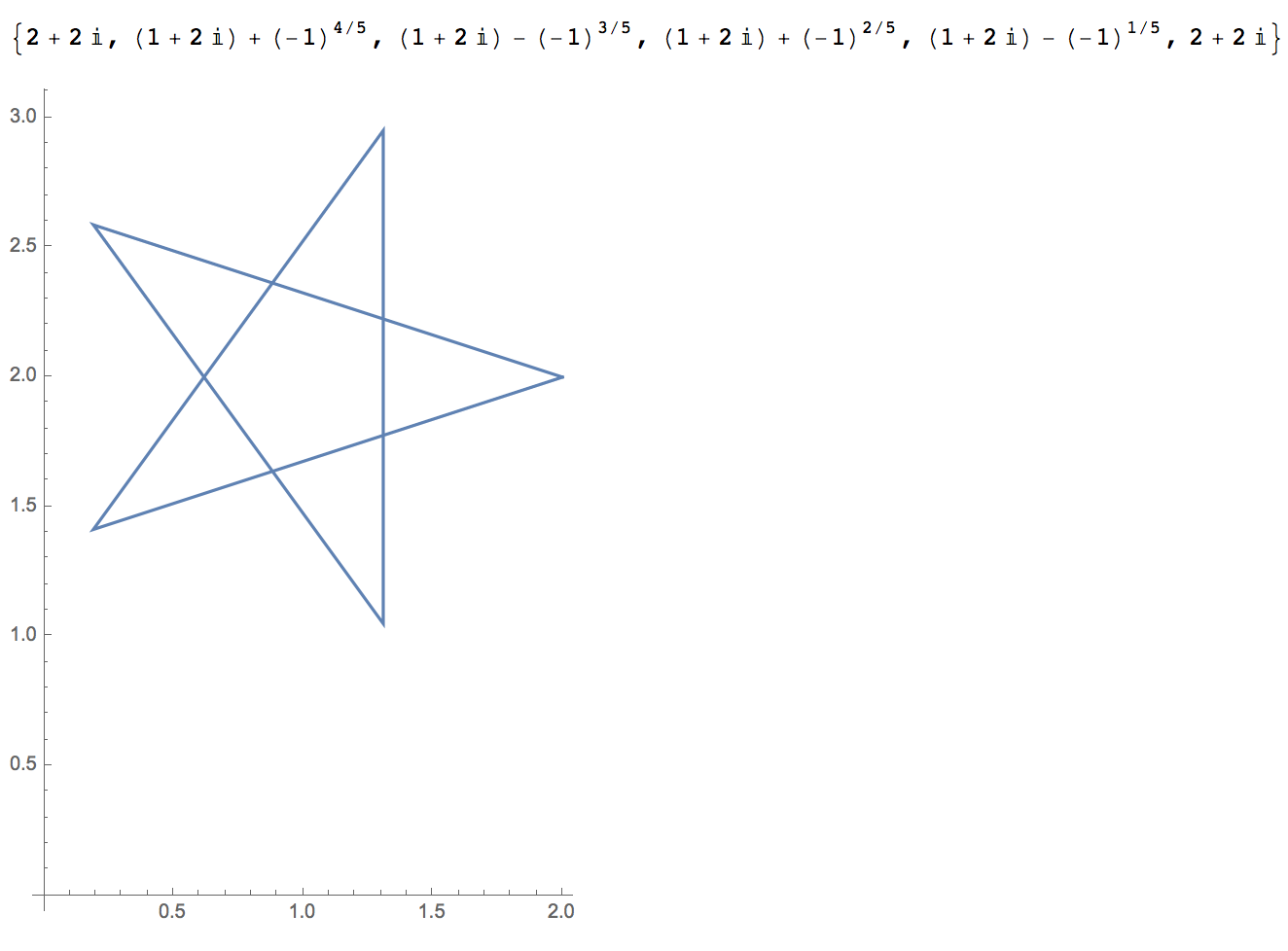
座標 $(1, 2)$ に相当する複素数 $1+2i$ を足すだけです。
compPts2 = compPts + (1 + 2 I)
ListLinePlot[{Re[#], Im[#]} & /@ compPts2, AspectRatio -> Automatic]
回転
30度($\frac{\pi}6$ ラジアン)回転は、複素数 $e^{\frac{\pi}6 i}$ を掛けるだけです。
compPts2 = E^(Pi/6 I) compPts
ListLinePlot[{Re[#], Im[#]} & /@ compPts2, AspectRatio -> Automatic]

複素数でできること
アフィン変換のうち
- せん断(skew)
- アスペクト比が変わる伸縮
は難しいですが、
- 平行移動
- 回転
- 拡大縮小(→定数倍で可能)
は四則演算の組み合わせだけで行えます。
Complex
複素数は
In[1] = FullForm[1 + 2 I]
Out[1] = Complex[1, 2]
となるように、頭部がComplexとなった要素で、
実部(Re)と虚部(Im)を取り出すには先ほどのように
{Re[#], Im[#]} &
という関数を通せばリストとして返ってきます。
Mathematicaにそこそこ詳しい人なら、
List @@ (1 + 2I)
とやって頭部ComplexをListに置き換えればいいじゃん、と
思いつくかもしれませんが、何故かその手は禁じられています。
(1 + 2I)[[{1, 2}]]
これも駄目です。
逆に、
Complex @@ {1, 2}
とやってリストを複素数にすることは可能です。
いっそのこと
reim[c_?NumberQ] := {Re[c], Im[c]}
reim[li_List] := {Re[#], Im[#]}& /@ li
とか関数作っちゃってもいいかと、記事を書きながら思いましたが、
もはや{Re[#],Im[#]}&の記述に慣れすぎてるので有用かどうかわかりません。
追記2018-12-15: バージョン10.1から ReIm 関数が導入されています。まんま!
ReIm—Wolfram言語ドキュメント
本当、役に立ちます。
来週執筆予定のコードゴルフ連載でも頻発することになると思いますが、
座標をリストとせず複素数とすることにより、一数値扱いになってある意味カプセル化的な役割を果たしているので、たとえばMap(/@演算)やFlattenを多用するときに、リストよりかなり都合がいいのです。
(場合によってはComplexやListの代わりにPointを使ってもいいかもしれませんが、あくまでもグラフィックスプリミティブなのでちょっと違う気がします。)
騙されたと思ってやってみてください。