はじめに
ツインドラゴン(Mathematicaショートフラクタルシリーズ) - Qiita
の数学的な話題をもう少し掘り下げました。
いくらか被る内容がありますがご容赦ください。
ツインドラゴンとは

ツインドラゴンは$2$進数の基数を$2$ではなく$1+i$($i$は虚数単位)として
計算することによって現れる図形です。
たとえば、$10$進数の$13$は$2$進数では$1101$と表せますが、
これは$1\times 2^3 + 1\times 2^2 + 0\times 2^1 + 1\times 2^0$と1桁毎に計算することにより
元の$13$という数を得ることができます。
ここで上記の基数$2$を$1+i$に置き換えると
$ 1×(1+i)^3 + 1×(1+i)^2 + 0×(1+i)^1 + 1×(1+i)^0$
$=1×(-2+2i) + 1×(2i) + 0×(1+i) + 1×(1)$
$=-1+4i$
となります。これが複素平面での座標$(-1,4)$になります。
$13$を冒頭の図で探してみると、"0"がある位置から
左に$-1$、上に$4$のところにありますよね。
このように、数字を0から順番に$1+i$を基数として数えることにより
冒頭の図のような数の平面ができます。
ツインドラゴンはD. Knuth氏が$-1+i$進数として世に知らしめた図形です。
本稿では$-1+i$進数ではなく$1+i$進数として議論を進めます。
今回の発見
冒頭の図の数字のある座標を0から順に数えると、
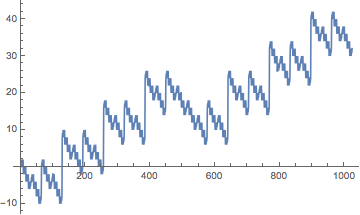
$x(n): 0, 1, 1, 2, 0, 1, 1, 2, -2, -1, -1, 0,\dots$
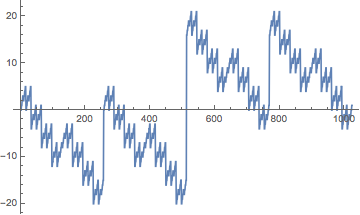
$y(n): 0, 0, 1, 1, 2, 2, 3, 3, 2, 2, 3, 3,\dots$
となります。
よく使う裏技で、
「オンライン整数列大辞典」を使って検索すれば、
一発解決できることがけっこうあります。
しかし、今回は検索に引っかかりませんでした。
(割と単純そうな数列なのに出ない、逆にこれはチャンス!)
$x$座標と$y$座標の列をそれぞれプロットすると下図のようなグラフになります。
2のべき乗で周期性がありそうですね。
なので、この数列$(x(n))$の2のべき乗番目$(x(2^n))$を取り出してみます。
すると
$x(2^n): 0, 1, 2, 2, 0, -4, -8, -8, 0, 16, 32, 32, \dots$
$y(2^n): 1, 1, 0, -2, -4, -4, 0, 8, 16, 16, 0, -32, \dots$
となりました。数列の値に0と2のべき乗が頻出していますね。
これを同じくしてオンライン整数列大辞典で検索したら引っかかりました。
どうやら$\sin(x) \exp(x)$と$\cos(x) \exp(x)$をそれぞれテイラー展開したときの係数の数列のようです。
http://oeis.org/A009545
http://oeis.org/A146559
なんで三角関数と指数関数が出てくるか謎の展開です。
そして、次の式が成立することが判りました(証明はしてませんが)。
$x(2^n) = 1 - y(2^n-1)$
$y(2^n) = x(2^n-1)$
この式を使えば、例えば先頭16要素の$x$と$y$の組から
それに続く16要素の$x$と$y$の組を
簡単に求められるということになります。
Mathematicaでは前回示したとおり、以下のように書けました。
Graphics[Point[
Transpose[{Re[#], Im[#]} &[
Nest[Join[#, # + 1 - Im[Last[#]] + Re[Last[#]] I] &, {0}, 10]
]]
]]
JavaScriptだと以下のように書けました。
var i, j;
var x = [0];
var y = [0];
var nextX = [];
var nextY = [];
for(j=0; j<4; j++) {
l = x.length-1;
for(i=0; i<x.length; i++) {
nextX[i] = x[i] + 1 - y[l];
nextY[i] = y[i] + x[l];
}
x = x.concat(nextX);
y = y.concat(nextY);
}
console.log(x);
console.log(y);
これを若干脚色した、canvas描画のプログラムをjsdo.itに投稿しました。
http://jsdo.it/butchi/twindragon
もっと短く書けるよ、とかあったら教えてください。