背景
1968年にアメリカ海軍の潜水艦スコーピオン号が消息を経ちました。この時の捜索に使われたのがベイズ推定を用いたベイズ捜索(Bayesian Search)です。飛行機やそのブラックボックスなどの捜索にも使われます。
変数定義
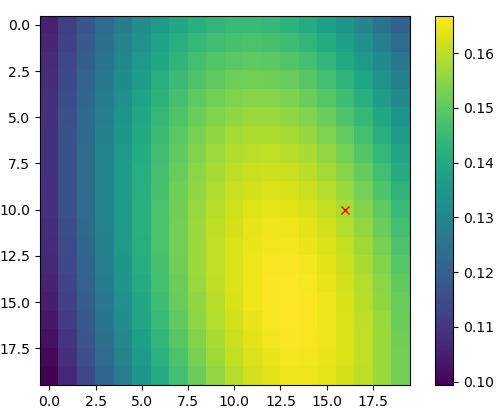
まず捜索エリアをセル分け定義します。ここでは簡易的に20x20のエリアとします。これに航路や最終報告された位置などの情報から、そのセルごとのあて推量の発見確率を、事前確率として以下のように確立分布で表現します。私の場合は正規分布で表現しました。赤いXは行方不明の捜索対象です。
ここで、以下のように変数を定義しておきます。
| 変数名 | 意味 |
|---|---|
| $i$ | セルのインデックス。上で示した捜索対象の場合$i=(16,10)$と表現する。 |
| $Y_i$ | iに捜索対象があるか否かの真値。ある場合1。ない場合0。 |
| $\pi_i$ | 上記のあて推量の事前確率。$P_r(Y_i=1)$ |
| $Z_i$ | iを捜索した結論。見つかった場合1。ない場合0。Yi=1であった場合に見つけられなかった場合も0。 |
| $p_i$ | iに捜索対象があった場合の発見確率。$P_r(Z_i=1|Y_i=1)$。この例ではどのセルも一律で0.1とする。実際には海底までの深さなどでセル毎に変更される。 |
$p_i$を定義している通り、この推定のポイントはそこに捜索対象があったとしても、捜索班の能力不足などにより見つけられない場合を考慮していることです。
さて、実際の捜索に移りましょう。
捜索アルゴリズム
- $\pi_i$が最大となるインデックス$i$の示すセルを捜索セルとする。
- セル$i$にて捜索対象が見つかった場合終了。見つからなかった場合、以下の通りに$\pi$を更新。
$\pi_i \leftarrow \frac{(1-p_i)\pi_i}{1-p_i\pi_i} $
i以外のセルjに対しては:
$\pi_j \leftarrow \frac{\pi_j}{1-p_i\pi_i}$ - 私の実装の場合、$\pi$がだんだん飽和し破綻したので、セル全体を合計して1.0になるように正規化しました。
- 1から繰り返し。
事前確率更新の様子
1000ステップを5ステップ飛ばしで描画させています。青い点がそのステップで捜索対象としたセルです。赤いXを捜索しても処理を終えていないのは、$p_i$が0.1だからです。10回に一回に捜索成功の判定となります。
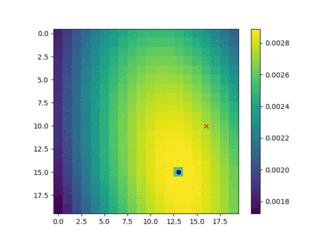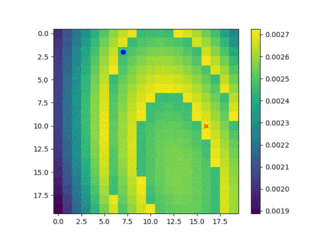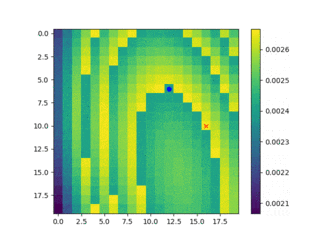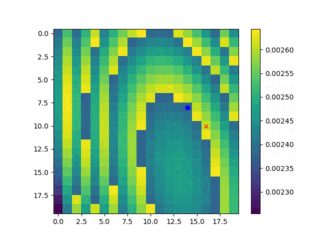
見つけられたかどうかはあまり重要としていないので、最後まで示していません。時間が在る時に全探索とのパフォーマンス比較をやってみます。
考察
人間が
「だいたいここらへんにあるはず」
という推測情報を使って、そのあたりからなんとなく順繰り捜索する場合も、
「あれ、おかしいな。こんなに推測から外れている場所に在るわけ無いぞ。
またあのあたりから探すか」
という具合に、エリアを全捜索するのでは無く、ある程度捜索し終わったらまた予測地点から捜索をスタートするという動きになると思います。
ですので上記のGIF画像から、
ベイズ捜索はそれをより無駄なく合理的に行う方法なのだと思いました。
上記のGIF結果を見ると、捜索点がセルの位置的にアチラコチラに触れているので、実際に捜索する場合は
セル内の捜索時間>>セル間の移動時間
でなければ、発見までの時間が無駄に長くなりますね。
コード
以下に上げました。
参考文献