自律的な量子誤り訂正符号の連接

スライド

スライドも公開しております

はじめに

近年、産業界からの量子コンピュータへの関心が高まっている。
量子コンピュータは素因数分解等の一部の問題に対して古典コンピュータと比べて高速に求解できると考えられており、材料開発や創薬等への応用が期待されている。
量子コンピュータを現実的な問題に実用化するためには100万個程度の量子ビットが必要と見積もられている一方、現在開発されている量子コンピュータのうち最大のものでもIBMの1121量子ビットにとどまっており、量子コンピュータの大規模化が不可欠である。

大規模な量子コンピュータを実現する上で最大の障害となるのが、量子ビットに生じるノイズである。
量子コンピュータと古典コンピュータの相違点として、量子重ね合わせや量子もつれといった量子力学に特有の性質の活用が挙げられるが、これらの性質はノイズに対して脆弱である。
量子コンピュータに発生するノイズに対処するためには、量子誤り訂正符号という技術が用いられる。
量子誤り訂正では複数の量子ビットを組み合わせて符号化を行うことで1量子ビット分の情報を保護する。
演算中の各ステップにおいて誤り検出・訂正を行うことにより、ノイズの影響を小さくしながら量子計算を行うことが可能となる。
また、近年では誤り検出や訂正のための測定や演算を明示的に行う必要のない誤り訂正手法である、自律的な量子誤り訂正符号も提案されている。
想定されるノイズを自律的に訂正できるような散逸を量子コンピュータに導入することで、誤り検出や訂正のための適応的な操作を行わなくてもよいというメリットがある。
人工的に制御された散逸は光学系での研究例が多いために、自律的な量子誤り訂正符号も光学系での研究事例が多い。

量子誤り訂正符号の性能を向上させるための手法として、符号の連接がある。
連接は二つの符号を組み合わせて一つの符号を作る手法であり、ノイズへの耐性を高めることができる。
理論的には、再帰的に量子誤り訂正符号を連接させることで、所望の精度までノイズの影響を小さくすることができる。
量子誤り訂正符号の連接は良く研究されたトピックだが、自律的な量子誤り訂正符号の連接は先行研究が少ない。
Pastawskiらによる研究¹では通常の量子誤り訂正符号に対応する自律的な量子誤り訂正符号の連接方法の一般論が与えられている。
また、Lieuらによる研究²ではそれぞれ自律的に位相反転、ビット反転を訂正する光学系とイジング模型の連接符号が考えられている。
自律的な量子誤り訂正符号の研究事例は光学系が多いため、光学系を含む自律的な量子誤り訂正符号の連接を考える必要があるが、そのような研究事例は多くなく、さらなる研究が望まれる。

そこで、本記事では自律的な量子誤り訂正符号の連接を考え、具体的な符号を構成することで実際にノイズ耐性が向上するのかを検証する。
その結果、通常の量子誤り訂正符号の連接と類似した手法で自律的な量子誤り訂正符号の場合にも連接を行うことができ、ノイズ耐性が向上することを確認した。

自律的な量子誤り訂正符号

本章では自律的な量子誤り訂正符号に関するレビューを行う。
以下の節で通常の量子誤り訂正符号、及び自律的な量子誤り訂正符号に関して紹介する。

量子誤り訂正符号

量子誤り訂正は符号化、誤り検出、誤り訂正という手順で行われる。
ここでは例として、ビット反転を訂正する3量子ビットを用いた符号を考える。
最初に、複数の量子ビットを用いて1量子ビットの情報を表現する、符号化を行う。
今回の場合では、1量子ビットの状態$\ket{0}_L,\ket{1}_L$をそれぞれ3量子ビットの状態$\ket{000},\ket{111}$を用いて表現する。
量子計算は符号化された状態に対して行うこととなり、例えば符号化された状態に対するビット反転操作は$X_L=X_1X_2X_3$となる。

計算中の各ステップで誤り検出・訂正を行うことでノイズから量子情報を保護する。
符号化された状態$\ket{000},\ket{111}$はどちらも$Z_1Z_2,Z_2Z_3$の固有値$+1$の固有状態であるため、これらの物理量に関する測定を行い、測定値が$-1$であればノイズが発生したと検知できる。
例えば$Z_1Z_2$の測定値が$+1$, $Z_2Z_3$の測定値が$-1$となった場合には、3番目の量子ビットにビット反転ノイズが発生したと推測されるため、$X_3$を作用させることで誤りを訂正できる。

複数の量子誤り訂正符号を組み合わせる連接を行うことで、ノイズへの耐性を上げることができる。
連接量子誤り訂正符号の一番簡単な例として、Shor符号が挙げられる。
これは先程紹介したビット反転を訂正する3量子ビットの符号と、位相反転を訂正する3量子ビットの符号$\ket{0}_L=\ket{+++},~\ket{1}_L=\ket{---} ~(\ket{\pm}=(\ket{0}\pm\ket{1})/\sqrt{2})$を連接した符号である。
ビット反転を訂正する3量子ビット符号は位相反転を訂正できなかったのに対し、連接を行うことによりShor符号はビット反転と位相反転の双方を訂正できる。
手順としては、片方の符号に現れる物理量子ビットに関する部分を、もう片方の符号化された量子ビットやその操作に置き換えればよい。
Shor符号の場合、符号化された状態は位相反転を訂正する符号に現れる$\ket{0},\ket{1}$をそれぞれ$\ket{000},\ket{111}$に置き換えればよく、

\begin{align}
\ket{0}_L&=\frac{(\ket{000}+\ket{111})(\ket{000}+\ket{111})(\ket{000}+\ket{111})}{2\sqrt{2}},  \\
\ket{1}_L&=\frac{(\ket{000}-\ket{111})(\ket{000}-\ket{111})(\ket{000}-\ket{111})}{2\sqrt{2}} 
\end{align}

となる。
他の操作に関しても同様であり、例えば誤り検出は位相反転を訂正する符号では$X_1X_2, X_2X_3$に関する測定を行えば良かったが、置き換えに伴いShor符号では$X_1X_2X_3X_4X_5X_6, X_4X_5X_6X_7X_8X_9$に関する測定により誤りを検出できる。

自律的な量子誤り訂正符号

量子誤り訂正では計算の各ステップで誤り検出・訂正を行う必要があるが、計算をコヒーレンス時間内に終わらせるため、これらの操作は高速に行わなければならない。
また、誤り検出や訂正の操作自体にもエラーが含まれてしまい、高速性と高精度を両立した機器の実現は実験的に難しい場合も多い。
この課題を解決するための誤り訂正の手法が、自律的な量子誤り訂正符号である。
自律的な量子誤り訂正では、誤り検出や訂正の代わりに散逸を導入し、符号化された状態が定常状態となるように散逸を設計する。

散逸を含む量子系の時間発展はLindblad方程式により記述できる：

\begin{align}
&\frac{d\rho}{dt}=\mathcal{L}(\rho)=-i[H,\rho]+\sum_i\mathcal{D}[L_i](\rho),  \label{eq:lindblad} \\
&\mathcal{D}[L_i](\rho)= L_i\rho L_i^{\dagger}-\frac{1}{2}\{L_i^{\dagger}L_i,\rho\}. \label{eq:dissipator}
\end{align}

ここで$\rho$は量子系の密度行列、$H$は系のハミルトニアンであり、散逸の効果は$\mathcal{D}(L_i)$で表される。
自律的な量子誤り訂正符号では散逸$L_i$を適切に設計することで、Lindblad方程式の定常状態が符号化された状態になるようにする。

散逸的な量子系の研究が光学系で多く行われていることから、自律的な量子誤り訂正符号も光学系での研究事例が多い。
例として、猫状態

\begin{align}
\ket{c_+}=\frac{1}{N_+}(\ket{\alpha}+\ket{-\alpha}),~\ket{c_-}=\frac{1}{N_-}(\ket{\alpha}-\ket{-\alpha}) \label{eq:cat}
\end{align}

が定常状態となる自律的な量子誤り訂正符号³を考える。
ここで$\ket{\alpha}=\sum_{n=0}^{\infty}\frac{\alpha^n}{\sqrt{n!}}\ket{n}$はコヒーレント状態で、$N_{\pm}=\sqrt{2(1\pm e^{-2|\alpha|^2})}$は規格化定数である。
この場合は光子の消滅演算子を$a$と書いた時に、$\lambda,\kappa_2\in\mathbb{R}$としてハミルトニアンと散逸をそれぞれ

\begin{align}
H=\lambda[a^2+(a^{\dagger})^2],~ L=\sqrt{\kappa_2}a^2 \label{eq:cat_lindbladian}
\end{align}

とすると、コヒーレント状態の振幅を

\begin{equation}
\alpha=e^{-i\pi/4}\sqrt{\frac{2\lambda}{\kappa_2}} \label{eq:amp_cat}
\end{equation}

とした時の猫状態の重ね合わせ

\begin{align}
\ket{\psi}=c_0\ket{c_+}_L+c_1\ket{c_-}_L~(|c_0|^2+|c_1|^2=1) \label{eq:cat_ss}
\end{align}

が定常状態となり、1量子ビットの情報を表すことができる。
猫状態は位相緩和$L_d=\sqrt{\kappa_d}a^{\dagger}a$に強い状態となっており、生じるエラー率は振幅$|\alpha|^2$に関して指数的に小さくなる。
そのため、上述した散逸は位相緩和を自律的に訂正する量子誤り訂正符号になっていると言える。
一方で猫状態は一光子ロス$L_1=\sqrt{\kappa_1}a$に対して脆弱であり、定常状態は量子ビットの構造を保てなくなる⁴。
そのため、この自律的な量子誤り訂正符号は一光子ロスは訂正することができない。

結果

本記事では光学系と量子ビット系で定義される自律的な量子誤り訂正符号の連接を考える。
本章では具体的に二つの自律的な量子誤り訂正符号の連接を行った後、\数値計算を行う上で計算量を減らす手法であるshifted Fock-basis法の概略を述べる。
その後、解析・数値計算を通して、本研究で扱う符号の誤り訂正能力を調べる。

本記事で扱う符号

初めに、連接に用いる二つの自律的な量子誤り訂正符号を紹介する。
光学系で定義される自律的な量子誤り訂正符号に関しては、前章で紹介した猫状態を用いる符号を用いる。
ハミルトニアンと散逸に関しても同様のものを考えるが、今後の計算のために、本章では同値な表現

\begin{equation}
\frac{d\rho}{dt}=\mathcal{D}[a^2-\alpha^2](\rho) \label{eq:timeevo_cat}
\end{equation}

を用いる。
$\alpha=e^{-i\pi/4}\sqrt{{2\lambda}/{\kappa_2}}$であり、二つの猫状態$\ket{c_{\pm}}$が重ね合わさった状態が定常状態となる。

量子ビット系で定義される自律的な量子誤り訂正符号は、ビット反転を自律的に訂正する3量子ビットの符号を用いる。
時間発展は

\begin{equation}
\frac{d\rho}{dt}=\mathcal{D}[P](\rho)+\sum_{i=1,2,3}\mathcal{D}[PX_i](\rho) \label{eq:timeevo_stabilizer}
\end{equation}

で与えられる。
$P=\ket{000}\bra{000}+\ket{111}\bra{111}$は符号化された状態への射影演算子で、第一項が符号化された状態の保護、第二項が各物理量子ビットにおけるビット反転エラーの訂正を表す。
実際、この時間発展では$\ket{000}$と$\ket{111}$の重ね合わせ状態が定常状態となる。

本研究では、これら二つの符号を連接した符号を考える。
3個のモードがある光学系を考え、それらの生成消滅演算子を$a_i, a_i^{\dagger}~(i=1,2,3)$とする。
本研究で考える自律的な量子誤り訂正符号の時間発展を以下で与える：

\begin{align}
\frac{d\rho}{dt}&=\mathcal{L}_{\mathrm{in}}(\rho)+\mathcal{L}_{\mathrm{out}}(\rho), \label{eq:lindblad_concatenation} \\
\mathcal{L}_{\mathrm{in}}(\rho)&=\sum_{i=1,2,3}\mathcal{D}[a_i^2-\alpha^2](\rho), \label{eq:dissipation_inner} \\
\mathcal{L}_{\mathrm{out}}(\rho)&=\mathcal{D}[P'](\rho)+\sum_{i=1,2,3}\mathcal{D}[P'a_i](\rho), \label{eq:dissipation_outer} \\
P'&=\ket{c_+c_+c_+}\bra{c_+c_+c_+}+\ket{c_-c_-c_-}\bra{c_-c_-c_-}. \label{eq:projector_concatenation}
\end{align}

$\mathcal{L} _ {\mathrm{in}}$は各モードの量子状態を猫状態$\ket{c _ {\pm}}$に自律的に保護する散逸である。
$\mathcal{L} _ {\mathrm{out}}$は3量子ビットの自律的な符号の場合と同様に、3モードの状態を自律的に揃える散逸である。
この表式は3量子ビットの自律的な符号に現れた$P,X _ i$を猫状態を用いた基底に置き換えることで得られる。
$P'$は$P$に対して$\ket{0}\rightarrow \ket{c_+},~\ket{1}\rightarrow\ket{c_-}$と置き換えればよく、$X_i$に関しては$a\ket{\alpha}=\alpha\ket{\alpha}$より$a\ket{c_{\pm}}\propto\ket{c_{\mp}}$となり、猫状態に対しては消滅演算子$a$がビット反転を引き起こすことを用いた。
$P'$は符号化された状態への射影を表し、実際$\ket{c_+c_+c_+},\ket{c_-c_-c_-}$を重ね合わせた状態は上式の定常状態となる。

Shifted Fock-basis法を用いた縮約

ノイズ下での誤り耐性を調べるために、各モードの一光子ロスを含む時間発展

\begin{align}
\frac{d\rho}{dt}=\mathcal{L}_{\mathrm{in}}(\rho)+\mathcal{L}_{\mathrm{out}}(\rho)+\kappa_1 \sum_{i=1,2,3}\mathcal{D}[a_i](\rho) \label{eq:timeevo_lossy}
\end{align}

を解き、その定常状態等を調べたい。
特に、誤り耐性が向上すると期待される、コヒーレント状態の振幅$|\alpha|$が大きい場合の計算を行いたい。
しかし、そのような状況は多光子状態を取り扱う必要があり、計算コストが高い。

この課題を解決するために、本研究ではshifted Fock-basis法⁵を用いる。
詳細は元論文⁵に譲り、本節では概略だけ述べる。
コヒーレント状態$\ket{\alpha}$は変位演算子$D(\alpha)=\exp[\alpha a^{\dagger}-\alpha^* a]$を用いて$\ket{\alpha}=D(\alpha)\ket{0}$と表される。
通常、光学系では光子数状態を基底として用いるが、shifted Fock-basis法では

\begin{equation}
\ket{\phi_{n,\pm}}=\frac{1}{\sqrt{2}}[D(\alpha)\pm(-1)^n D(-\alpha)]\ket{n} \label{eq:basis_sfb}
\end{equation}

を基底として用いる。
この基底上で消滅演算子は

\begin{equation}
a\ket{\phi_{n,\pm}}=\sqrt{n}\ket{\phi_{n-1,\mp}}+\alpha\ket{\phi_{n,\mp}} \label{eq:annihilation_sfb}
\end{equation}

と作用するため、先程の基底を用いて行列表示すると

\begin{equation}
a=X\otimes (b+\alpha) \label{eq:annihilation_rep}
\end{equation}

と表される。
$b$は$\ket{\phi_{n,\pm}}$に対する消滅演算子である：$b\ket{\phi_{n,\pm}}=\sqrt{n}\ket{\phi_{n-1,\pm}}$.

$\ket{\phi_{n,\pm}}$は規格化されていない上に直交しないため、厳密には$\ket{\phi_{n,\pm}}$を規格直交化した基底での表示を求める必要がある。
しかし振幅の絶対値$|\alpha|$が十分大きい場合には$\ket{\phi_{n,\pm}}$はほぼ規格直交するため、先程の表示をそのまま用いることができる。
特に$|\alpha|$が十分大きければ$\ket{c_{\pm}}\simeq \ket{\phi_{0,\pm}}$である。
これらの表式を用いて1光子ロスを含む時間発展を書き換えると、

\begin{align}
\frac{d\rho}{dt}=\sum_{i=1,2,3}\mathcal{D}[I\otimes (b_i^2+2\alpha b_i)](\rho)+\mathcal{D}[P'](\rho)+\sum_{i=1,2,3}\mathcal{D}[P'\{X_i\otimes (b_i+\alpha)\}](\rho)+\kappa_1 \sum_{i=1,2,3}\mathcal{D}[X_i\otimes (b_i+\alpha)](\rho) \label{eq:timeevo_lossy_sfb}
\end{align}

を得る。
以降$b$に対する真空状態を$\ket{0}'$と書き、分かりやすさのために$\ket{\phi_{n,\pm}}$の符号に対応する状態の基底を$\ket{0},\ket{1}$と書くこととする。
この表記を用いると$P'=(\ket{000}\bra{000}+\ket{111}\bra{111})\otimes\ket{000}'\bra{000}'=P'_g\otimes \ket{000}'\bra{000}'$となるため、$b_i$や$P$は$n$の値を小さくする方向にのみ働く。
そのため、初期状態が$n=0$の項のみで構成され、$\rho(0)=\rho_g(0)\otimes\ket{000}'\bra{000}'$と表される場合には、時間発展した状態も$n=0$の項のみで表される：$\rho(t)=\rho_g(t)\otimes\ket{000}'\bra{000}'$.
$\rho_g$に対する縮約した時間発展を求めると、

\begin{align}
\frac{d\rho_g}{dt}=\kappa_{\mathrm{out}}\left\{\mathcal{D}[P'_g](\rho_g)+|\alpha|^2\sum_{i=1,2,3}\mathcal{D}[P'_gX_i](\rho_g)\right\}+\kappa_1|\alpha|^2\sum_{i=1,2,3}\mathcal{D}[X_i](\rho_g) \label{eq:timeevo_sfb}
\end{align}

となる。
上式は3量子ビットに対する時間発展となり、元の式と比較して状態の次元を大きく減らすことができ、数値計算を行う上で計算量を削減できる。
以降ではこちらの式を解析し、本記事で扱う符号の誤り訂正能力を調べる。

数値計算

ここでは一光子ロスが存在する場合に符号化された状態が保たれる度合いにより、符号性能を評価する。
時間発展させた状態$\rho_g(t)$と初期状態$\ket{\psi_0}$の近さを測る指標として、本研究ではフィデリティ

\begin{align}
F(\rho_g(t),\ket{\psi_0})=\bra{\psi_0}\rho_g(t)\ket{\psi_0} \label{eq:fidelity}
\end{align}

を用いる。
定義よりフィデリティは0以上1以下の値を取り、値が1に近いほど二つの状態は近いと評価される。

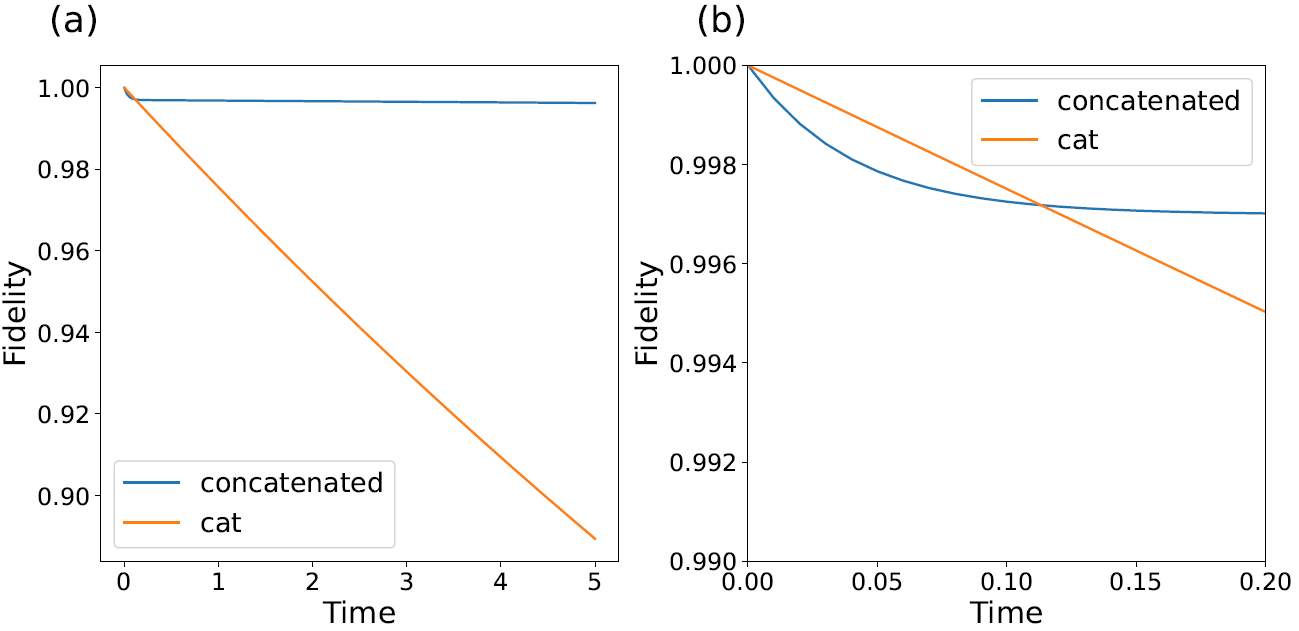
時間発展した状態と初期状態のフィデリティを計算した結果を下の図に示す。

比較のために、連接を行っていない単一の猫状態を符号状態とするshifted Fock-basisの時間発展

\begin{align}
\frac{d\rho_g}{dt}=\kappa_1|\alpha|^2\mathcal{D}[X](\rho_g) \label{eq:timeevo_cat_lossy}
\end{align}

についても、初期状態とのフィデリティの時間発展を計算した。
各種パラメータや時間は$\kappa_{\mathrm{out}}$で規格化し、$|\alpha|=5,\kappa_1=0.001$とした。
図(a)を見ると、連接を行っていない場合(橙線)にはフィデリティは時間が経過するにつれて小さくなっているのに対し、連接を行った場合(青線)ではある程度の時間が経過するとフィデリティの値は1に近い値に収束する。
この結果は、連接を行うことにより符号がビット反転を自律的に訂正できるようになったことを示す。

実用的には、量子コンピュータに発生するノイズを最小化するために、その動作は高速に行われる場合が多い。
そのような場合には、短時間でノイズが発生する確率であるエラー率も符号の性能評価に用いられる。
例えば猫状態の符号の場合には、短時間の時間発展は

\begin{align}
\rho_g(t)\simeq (1-p_X)\rho_g(0)+p_XX\rho_g(0)X,~p_X=\kappa_1|\alpha|^2t \label{eq:cat_lossy_sol}
\end{align}

で与えられるため、エラー率$p_X$が初期状態との乖離を測る指標となる。
上式では第二項は初期状態とのフィデリティに寄与しないため、短時間領域でのフィデリティの時間発展からエラー率を推測することができる。
図(b)に示すように、短時間領域では連接した場合の方がフィデリティが小さい時間領域が存在するが、時間が経過するとその減少が緩やかになる。
この振る舞いは時間発展の方程式から理解できる。
1光子ロスを表す項以外は符号化された状態に対して寄与しないため、符号化された状態を初期状態として時間発展を行うと、短時間での状態の時間発展は

\begin{align}
\rho_g(t)\simeq (1-p_X)\rho_g(0)+p_X\sum_{i=1,2,3}X_i\rho_g(0)X_i \label{eq:concatenation_sol}
\end{align}

で与えられる。
そのため、連接して量子ビット数が増加したことに伴ってエラー源が増えたことが原因と考えられる。
一方、時間が経過すると1光子ロスにより発生したエラーが$\mathcal{L}_{\mathrm{out}}$により自律的に訂正され、フィデリティの値は下げ止まる。

まとめ

本記事では光学系と量子ビット系における自律的な量子誤り訂正符号の連接を考えた。
先行研究²の結果と本研究の解析・数値計算結果を合わせ、自律的な量子誤り訂正符号の場合にも、外側の符号に現れる演算子を内側の符号化された状態に対する論理的な操作に置き換えることで連接が行えることが示唆された。
自律的な量子誤り訂正符号においても、連接を行うことによりノイズ耐性を高められる他、エラー率に関しても改善する領域が存在することが数値計算により確認できた。

今後の展望としては、本記事で用いた連接方法の一般化を行うことが考えられる。
本記事では扱わなかったが、実際の自律的な量子誤り訂正符号ではゲート操作も必要となるため、ゲート操作も含めた連接手法の確立が求められる。
また、自律的な量子誤り訂正符号を実装する上で、緩和時間やエラー率が現実的なパラメータ設定に対してどのような値をとるのかも調べる必要があるが、今後の課題としたい。

1. F. Pastawski, L. Clemente, and J. -I. Cirac, Phys. Rev. A 83, 012304 (2011). ↩

2. S. Lieu, Y. -J. Liu, and A. V. Gorshkov, Phys. Rev. Lett. 133, 030601 (2024). ↩ ↩²

3. M. Mirrahimi, Z. Leghtas, V. V. Albert, S. Touzard, R. J. Schoelkopf, L. Jiang, and M. H. Devoret, New J. Phys. 16 045014 (2014). ↩

4. S. Lieu, R. Belyansky, J. T. Young, R. Lundgren, V. V. Albert, and A. V. Gorshkov, Phys. Rev. Lett. 125 240405 (2020). ↩

5. C. Chamberland, K. Noh, P. Arrangoiz-Arriola, E. T. Campbell, C. T. Hann, J. Iverson, H. Putterman, T. C. Bohdanowicz, S. T. Flammia, A. Keller, G. Refael, J. Preskill, L. Jiang, A. H. Safavi-Naeini, O. Painter, and F. G. S. L. Brandão, Phys. Rev. X 3, 010329 (2022). ↩ ↩²