概要
8/10~8/16に行われてたUnity1週間ゲームジャム に参加してみました。
決められたお題で1週間でゲームを作って公開するという催しなのですが、今回のお題は「ふえる」というもので、それにちなんだゲームを作りました。
ふえる というテーマで真っ先に思いつくものといえば、当然ライフゲームですよね?
「なんで?」とか聞かないでください。論理的なこと言う人あたい嫌いです。
ちなみに、こんなの作りました。
乳酸菌工場
https://unityroom.com/games/nyusankinkoujou
で、以前からビットボードについての勉強がしたいなぁと思ってたので、せっかくだからそれ使って作ってみることにしました。
この投稿で、ビットボードの仕組みみたいな勉強結果を(自分があとで忘れてもまた思い出せるために)掲載します。
なお、この投稿はライフゲームのルールについては知ってる前提で記載してます。
まだご存じない方は、以下の動画をパート1から全部観て下さい。本当にすっごく面白い動画なので。観ない人あたい嫌いです。
ビットボードとは
一言でいうと、複数のマス目をビットで表してまとめて計算する やり方みたいな感じです。
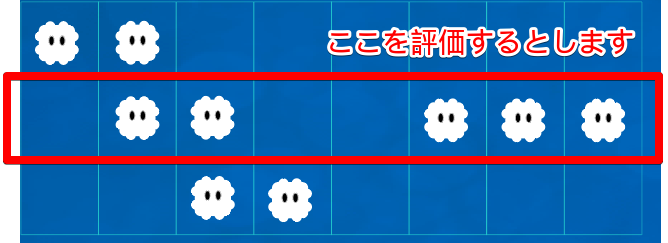
たとえば、ライフゲームで以下のような配置となっているとします。
その後もこちらの配置を使って説明します(面倒なので3×8の小さい盤面だとしますね)
Q:これはなんですか?
A:ライフゲームをかわいくしたやつです。かわいいね?
これを8ビットで表すと、以下のようになります。
(列はA,B,C...、行は1,2,3とふってます)
| - | A | B | C | D | E | F | G | H | uintの数値 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 192 |
| 2 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 103 |
| 3 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 48 |
(最初だけわかりやすく数値を記載してますが、以降はビット値のみ記載します)
こんな感じで配置をビットで表現するというのがビットボードです。
このように表現することで、ビット演算を使って複数のマス目をまとめて計算するということが可能となります。
8ビットなら8マス、64ビットなら64マス同時に計算ができます。
たとえば、ゲームでマス目を表現する場合、単純な方法として最初に思いつくのは普通に二次元配列(またはMap / Dictionary)などを使う方法かと思いますが、その場合盤面の状態を1マスごとに計算することになるため、マス目が多くなるとどうしてもパフォーマンス的な問題が出てきてしまいます。
(過去に8×8マスの小さいボードゲームをその方法で作ってみたのですが、AIに4手先を計算させるだけでも著しくパフォーマンスが下がったのを覚えてます)
特にライフゲームの場合は本来フィールドの制限がなく、巨大なものを作ろうとすると配列での計算は、処理速度的にもメモリ的にも早く限界に到達します。
それを代わりにビットボードで表現することで、高速化および省メモリ化を実現できるわけですね。
上記だと8ビットですが、64ビットの数値で表現をすれば、単純計算で64倍の高速化、および省メモリ化が実現できます。
あたい、そういう論理的な話好きよ。
(もちろん実際は単純に64倍にはなりませんが)
そんなわけで、まずは計算部分のコードを
多分以下を見て理解できる方はあまりいないかもしれませんが(そもそも変数の意味とかもよくわからないと思いますし)、この後説明していきます。
public class Lifegame {
private static readonly int shift = 7;
private static int next(List<int> board, int y) {
// 現在の評価位置
int c = board[y];
// 西
int w = c >> 1;
// 東
int e = c << 1;
// 北
int n = y == 0 ? 0 : board[y - 1];
// 北西
int nw = n >> 1;
// 北東
int ne = n << 1;
// 南
int s = y >= shift ? 0 : board[y + 1];
// 南西
int sw = s >> 1;
// 南東
int se = s << 1;
// 評価数(0~8)
int s0, s1, s2, s3; //, s4, s5, s6, s7, s8;
s0 = ~(nw | n);
s1 = nw ^ n;
s2 = nw & n;
s3 = ne & s2;
s2 = (s2 & ~ne) | (s1 & ne);
s1 = (s1 & ~ne) | (s0 & ne);
s0 = s0 & ~ne;
//s4 = w & s3;
s3 = (s3 & ~w) | (s2 & w);
s2 = (s2 & ~w) | (s1 & w);
s1 = (s1 & ~w) | (s0 & w);
s0 = s0 & ~w;
// s5 = e & s4;
// s4 = (s4 & ~e) | (s3 & e);
s3 = (s3 & ~e) | (s2 & e);
s3 = (s3 & ~e) | (s2 & e);
s2 = (s2 & ~e) | (s1 & e);
s1 = (s1 & ~e) | (s0 & e);
s0 = s0 & ~e;
// s6 = sw & s5;
// s5 = (s5 & ~sw) | (s4 & sw);
// s4 = (s4 & ~sw) | (s3 & sw);
s3 = (s3 & ~sw) | (s2 & sw);
s3 = (s3 & ~sw) | (s2 & sw);
s2 = (s2 & ~sw) | (s1 & sw);
s1 = (s1 & ~sw) | (s0 & sw);
s0 = s0 & ~sw;
// s7 = s & s6;
// s6 = (s6 & ~s) | (s5 & s);
// s5 = (s5 & ~s) | (s4 & s);
// s4 = (s4 & ~s) | (s3 & s);
s3 = (s3 & ~s) | (s2 & s);
s3 = (s3 & ~s) | (s2 & s);
s2 = (s2 & ~s) | (s1 & s);
s1 = (s1 & ~s) | (s0 & s);
s0 = s0 & ~s;
// s8 = se & s7;
// s7 = (s7 & ~se) | (s6 & se);
// s6 = (s6 & ~se) | (s5 & se);
// s6 = (s6 & ~se) | (s5 & se);
// s5 = (s5 & ~se) | (s4 & se);
// s4 = (s4 & ~se) | (s3 & se);
s3 = (s3 & ~se) | (s2 & se);
s3 = (s3 & ~se) | (s2 & se);
s2 = (s2 & ~se) | (s1 & se);
s1 = (s1 & ~se) | (s0 & se);
s0 = s0 & ~se;
return (~c & s3 ) | ( c & ( s2 | s3 ));
}
}
コードは、こちらを丸パクリ大いに参考にしました。
東大マイコンクラブ駒場祭部誌2018
http://www.komaba.utmc.or.jp/documents/UTMC201811.pdf
(掲載場所: http://www.komaba.utmc.or.jp/?page_id=39)
コメントアウトしてる部分は、処理的には不要と思われる部分です。ただ説明の際にはある方がわかりやすいので記載してます。
ビット演算に関して
説明をするにあたって、ビット演算の知識は必要不可欠なのでチートシートを記載しておきます。
詳しくは、ググって理解する方が良いかと思います。
| 操作 | 説明 | 例 |
|---|---|---|
| x | y | x と y のビットで、どちらか一方が1の場合は1、そうでない場合0を設定 (OR) | x = 0b0100; y = 0b1000; assert(x | y == 0b1100); |
| x & y | x と y のビットで、どちらも1の場合は1、そうでない場合は0を設定 (AND) | x = 0b0110; y = 0b1100; assert(x & y == 0b0100); |
| x ^ y | x と y のビットで、どちらも0または1の場合は1、そうでない場合は0を設定 (XOR) | x = 0b0110; y = 0b1100; assert(x ^ y == 0b0101); |
| ~x | x のビットを反転 (NOT) | x = 0b0110; assert(~x == 0b1001); |
| x << y | x のビットをyの数値分左にずらす (左シフト。右端に0が足され、左端にあふれたビットは消える) |
x = 0b1101; assert(x << 1 == 0b1010); |
| x >> y | x のビットをyの数値分右にずらす (右シフト。左端に0が足され、右端にあふれたビットは消える) |
x = 0b1101; assert(x >> 1 == 0b0110); |
| -x | ~x + 1 と同じ (補数。負の数のコンピューター上での表現。unsignedでも使える) |
x = 0b1101; assert(-x == 0b0011) (0b1101 + 0b0011 は、 全ての1が繰り上がって0b0000 = 0となる) |
| x & -x | 右端の1のみを抽出する | x = 0b0110; assert(-x == 0b1010); assert(x & -x, 0b0010); |
一部使ってないのも書きましたが、これらがわかってたら後は読めるかと思います。
ライフゲームにおけるビットボードの計算
上記コードの説明をしていきます。
結構長ったらしいコードですが、やっていることは結構単純です。
なお、上のコードは1行が32ビットで収まること=1つの数値に1行分のデータが収まることを前提としています。実際のライフゲームみたく、1つの行も無限にあるようなケースは「東大マイコンクラブ駒場祭部誌2018」に記載されているコードのように board を多次元にする必要があります。
前置きしちゃったので、改めて。やってることは以下の通りです。
- 評価したい行と、その周囲8マスの状態を取得する(変数c~se)
- それぞれのマスの「生」のマスの数を計算し、格納する(s0~s8の計算)
- ライフゲームのルールにのっとって、生死を判別する(returnの部分)
それぞれ順を追って説明します。
周囲8マスの状態を取得する
こちらの処理です。
// 現在の評価位置
int c = board[y];
// 西
int w = c >> 1;
// 東
int e = c << 1;
// 北
int n = y == 0 ? 0 : board[y - 1];
// 北西
int nw = n >> 1;
// 北東
int ne = n << 1;
// 南
int s = y >= shift ? 0 : board[y + 1];
// 南西
int sw = s >> 1;
// 南東
int se = s << 1;
こちらでやっているのは、ボードの行の取得と、それぞれの右シフト、左シフトです。
こうした結果どうのようなデータが格納されるか、最初の例でみてみましょう。
この2行目のデータを「c」とします。すると、「c」「n」「s」には以下のデータが格納されます。
| 変数 | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| n | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| c | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| s | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
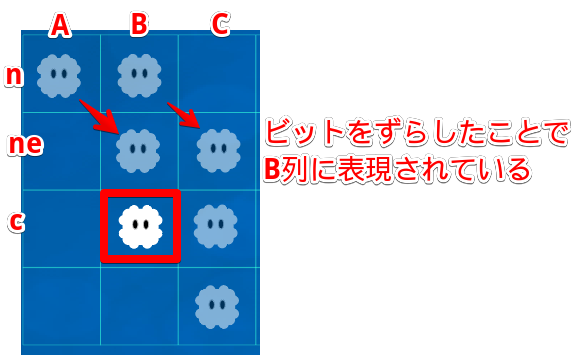
そして、その後「cw」「ce」などは、ビットを右、左それぞれに移動させています。すると以下のようなデータが入ります。
| 変数 | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| cw | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| c | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 |
| ce | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
n,sに対しても同じことをしています。一度全部記載しますね。
(みやすくするため、0はちょっとなくしておきます)
| 変数 | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| nw | 1 | |||||||
| n | 1 | 1 | ||||||
| ne | 1 | 1 | ||||||
| cw | 1 | 1 | 1 | 1 | 1 | |||
| c | 1 | 1 | 1 | 1 | 1 | |||
| ce | 1 | 1 | 1 | 1 | ||||
| sw | 1 | 1 | ||||||
| s | 1 | 1 | ||||||
| se | 1 | 1 |
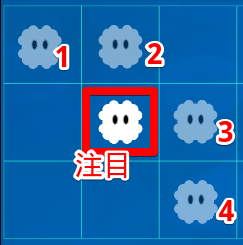
ここで、たとえば**「c」の「B」列**に注目します。画像でいうと以下の部分です。
この注目しているセルの周りの生きたセル「1」~「4」は、上記のB列に表現されていることがわかるでしょうか。
B列に表現されている生きたセルと、実際のセルの場所をマッピングすると、以下のような感じです。
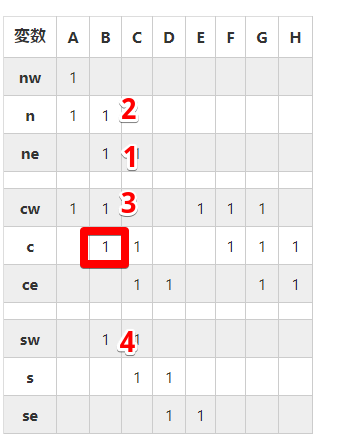
「n」は、そのまま一つ上の行を表しているのでそのまま真上の生きたセルの値が入っています。
「ne」は、それぞれビット値をひとつ右側にずらしています。そのため生きたセルも右に一つずれ、「1」のセルがB列に表現されています。
「3」も同様に「c」のビット値を左にずらしているため、C列にあったセルがB列に表現されています。
その他のセルもすべて同様で、「B列」のビット値には、注目している箇所と周囲のセルの生死がすべて表現されています。
もちろん上記ではB列のみに注目していますが、同じことがすべての列で行われています。
なので、あとはそれぞれの列に存在している「1」の数を求めるだけでいいわけですね。
それぞれのマスの「生」のマスの数を計算し、格納する
以下の処理部分です。
// 評価数(0~8)
int s0, s1, s2, s3; //, s4, s5, s6, s7, s8;
s0 = ~(nw | n);
s1 = nw ^ n;
s2 = nw & n;
s3 = ne & s2;
s2 = (s2 & ~ne) | (s1 & ne);
s1 = (s1 & ~ne) | (s0 & ne);
s0 = s0 & ~ne;
//s4 = w & s3;
s3 = (s3 & ~w) | (s2 & w);
s2 = (s2 & ~w) | (s1 & w);
s1 = (s1 & ~w) | (s0 & w);
s0 = s0 & ~w;
// s5 = e & s4;
// s4 = (s4 & ~e) | (s3 & e);
s3 = (s3 & ~e) | (s2 & e);
s3 = (s3 & ~e) | (s2 & e);
s2 = (s2 & ~e) | (s1 & e);
s1 = (s1 & ~e) | (s0 & e);
s0 = s0 & ~e;
// s6 = sw & s5;
// s5 = (s5 & ~sw) | (s4 & sw);
// s4 = (s4 & ~sw) | (s3 & sw);
s3 = (s3 & ~sw) | (s2 & sw);
s3 = (s3 & ~sw) | (s2 & sw);
s2 = (s2 & ~sw) | (s1 & sw);
s1 = (s1 & ~sw) | (s0 & sw);
s0 = s0 & ~sw;
// s7 = s & s6;
// s6 = (s6 & ~s) | (s5 & s);
// s5 = (s5 & ~s) | (s4 & s);
// s4 = (s4 & ~s) | (s3 & s);
s3 = (s3 & ~s) | (s2 & s);
s3 = (s3 & ~s) | (s2 & s);
s2 = (s2 & ~s) | (s1 & s);
s1 = (s1 & ~s) | (s0 & s);
s0 = s0 & ~s;
// s8 = se & s7;
// s7 = (s7 & ~se) | (s6 & se);
// s6 = (s6 & ~se) | (s5 & se);
// s6 = (s6 & ~se) | (s5 & se);
// s5 = (s5 & ~se) | (s4 & se);
// s4 = (s4 & ~se) | (s3 & se);
s3 = (s3 & ~se) | (s2 & se);
s3 = (s3 & ~se) | (s2 & se);
s2 = (s2 & ~se) | (s1 & se);
s1 = (s1 & ~se) | (s0 & se);
s0 = s0 & ~se;
この中で、それぞれ「1」の数をs0~s8の中に入れています。
s0は、生きたセルの数が0の列を表現しています。
s3は、生きたセルの数が3の列を表現しています。
(s4~s8は不要そうだったのでコメントアウトしてますが、コメントアウトを外せば生きたセルの数が入ってきます)
どうしてこれで計算ができるのでしょう。
例として、最初の3行にまずフォーカスしてみます。
s0 = ~(nw | n);
s1 = nw ^ n;
s2 = nw & n;
ここのs0は、nwとnのどちらかで1が立っている箇所を反転させています。
実際の数でみてみると、以下の感じです。
| 変数 | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| nw | 1 | |||||||
| n | 1 | 1 | ||||||
| nw | n | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| ~(nw | n) | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
たしかに 「n」と「nw」だけに注目したとき、C列以降は生きたセルは存在していません。それが ~(nw | n) にて表現できています。
s1、s2も同じようにしています。
s1はXORの処理であり、「どちらかが1の場合は1、どちらも1、またはどちらも0の場合は0」にする処理です。
s2はANDの処理であり、「どちらも1の場合は1、それ以外なら0」が入ります。
まとめると、こういう値が入ります。
| 変数 | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| nw | 1 | |||||||
| n | 1 | 1 | ||||||
| s0 = ~(nw | n) | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| s1 = nw ^ n | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| s2 = nw & n | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
見事に表現できてます。すうがくってしゅごい。
では、その下の処理を見てみます。
s3 = ne & s2;
s2 = (s2 & ~ne) | (s1 & ne);
s1 = (s1 & ~ne) | (s0 & ne);
s0 = s0 & ~ne;
ここでは、得られた値から3つ存在している場所を得、そのあとは北東の値を使ってs0~s2を上書きしています。
s2に関しては、「s2にフラグが立ち、かつ北東にフラグが立っていない」か、「s1と北東両方にフラグが立っている」場所にフラグを立てています。
どちらも「2個しかない」ことを表現していることがわかるかと思います。
s2にフラグが立っている箇所は暫定的な2です。その状態で「北東にフラグが立っていない」箇所はすなわち「2個」しかないということになります。
s1にフラグが立っている箇所は暫定的に1であり、かつ「北東にフラグが立っている」箇所は1 + 1 = 「2個」存在しているということになります。
同様のことをs1でも計算しています。
まとめると、この段階で以下のような数値が入ります。
| 変数 | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| nw | 1 | |||||||
| n | 1 | 1 | ||||||
| ne | 1 | 1 | ||||||
| s0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| s1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| s2 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| s3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
その後は、同じような計算をそれぞれで繰り返しています。
ライフゲームのルールにのっとって、生死を判別する
最後は以下の部分です。
return (~c & s3 ) | ( c & ( s2 | s3 ));
もうきっとみんなビット演算マスターになってると思うので、こちらは何してるかいわずもがなでしょう。
そうだね、(~c & s3) 部分は合計3個ある死んでるセルに生フラグを立て、( c & ( s2 | s3 )) 部分は周りが2個か3個生きたセルがある生きてるセルを生存させてるんだね。
そして、それ以外は0(死フラグ)を立ててます。
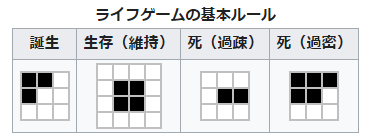
つまりはWikipediaにある以下のルールで生死を決定しています。
突き詰めればルールを1行で表せるなんてすごいですねぇ。すごいなぁ。すごいよねぇ?
まとめ
というわけで、ビットボードの解説でした。
応用すると、オセロとかでも**「白の場所」「黒の場所」それぞれのビットボードを作成してそれぞれで計算する**みたいなことをすることで、0と1以上の状態もビットボードで計算することができそうです。また更に応用するとαβ法といったAIのアルゴリズムもビットボードで表現することができるみたいです(そのあたりはちゃんと調べてないけど)。
ビット演算って具体的な数値がわかりづらいのでちょっと敬遠しがちですが、やってることは0と1を加工するだけなので、結構単純なんですね。