2024年後半、プライベートでChatGPTと新しいペンシルパズルを作ることに挑戦してきました。未発表のパズルについて、こちらの記事で発表しようと思います。
さて、この記事では、まず初めに私とChatGPTが協力してパズルのルールや問題生成コードを作成した、「ダブりはみえない」と名付けたパズルをご紹介します。(シンプルなルールなので、全く同じパズルをすでに考案している人がいるかもしれません。ペンシルパズルで同じルールがあるかどうかを、どのように調べればよいかが難しいのです。)
その後、どのようにChatGPTを活用したのかについてと、今回使用した範囲でのZ3ソルバーについての解説を行います。
パズル「ダブりはみえない」の概要
このパズルでは、すべてのマスに数字が書かれた正方形のグリッドが与えられます。あなたの目標は、いくつかのマスを黒く塗りつぶして、以下のルールを満たすことです。
ルール
- 黒マスの配置:
- 数字が書かれたマスを塗りつぶし、黒マスにすることができます
- 黒マス同士は縦横に隣接してはいけません(斜めに隣接することは可能です)
- 白マスの連結性:
- 黒く塗られていないマスを白マスと呼びます。すべての白マスは、縦横で連続した一つの領域になる必要があります。つまり、黒マスによって盤面が分断されてはいけません
- 数字に関する制約:
- 縦または横の方向に、外壁または黒マスで挟まれた白マスの領域において、同じ数字は1度しか現れてはいけません
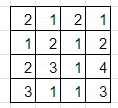
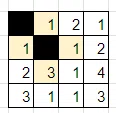
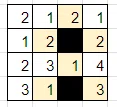
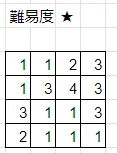
例題
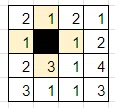
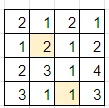
盤面の隅から解いていくのが良いでしょう。まず、2行目2列目の「2」に注目します。このマスが黒マスだと仮定してみましょう。黒マスは縦横に連続しないので、このマスの上下左右は白マスになります。
左上の「2」が白マスだとすると、ルールの数字に関する制約から、同じ数字が2回現れてはいけないため、2か所の「2」は黒マスになります。
すると、黒マスによって盤面が分断されてしまい、ルールの白マスの連結性を満たさなくなってしまいます。
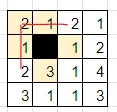
これは失敗なので、今度は左上の「2」を黒マスだと仮定してみます。
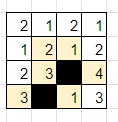
2行目3列目の「1」が白マスになったので、数字に関する制約から、3行目3列目の「1」が黒マスになります。黒マスの隣接制約から、その上下左右は白マスになります。
4行目3列目の「1」が白マスになったので、数字に関する制約から、4行目2列目の「1」が黒マスになりますが、これによって黒マスが盤面を分断してしまいます。
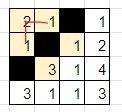
長い旅でしたが、左上の2は黒マスでも白マスでも失敗となり、最初の過程が間違いだったことがわかりました。つまり、2行目2列目の「2」は白マスです。慣れてくると、ここまで頭の中でできます。
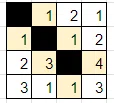
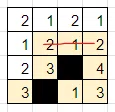
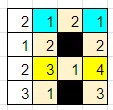
次は、4列目3行目の「1」に注目してみましょう。これを白マスだと仮定してみます。
数字の制約から、2か所の「1」が黒マスになります。黒マスの隣接制約から、黒マスの上下左右が白マスになります。
黒マスで盤面が分断されてはいけないので、2行目4列目の「2」と4行目4列目の「3」は白マスです。すると、2行目で「2」が2回出てくる領域が出てきてしまい、数字の制約を満たせなくなります。またまた仮定が間違っていたことがわかります。
仮定が間違っていたので、4列目3行目の「1」は黒マスが正しいです。隣接するマスは白マスです。
3行目3列目の「1」が白マスなので、数字の制約から、2行目3列目の「1」は黒マスです。
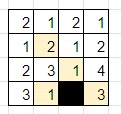
数字の制約から、1行目の「1」は少なくともどちらかは黒マスです(下図水色)すると、3行目2列目や3行目4列目(下図黄色)が黒マスだと、黒マスによって盤面が分断されてしまうことがわかります。これら黄色のマスは両方白マスです。
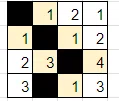
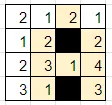
白マスを確定すると下記のようになります。
2列目、数字の制約から「1」は黒マスです。
黒マスによって盤面が分断されないように、2か所の「1」が白マスだとわかります。後は数字の制約から、「2」が黒マスになります。
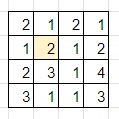
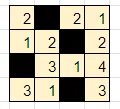
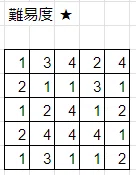
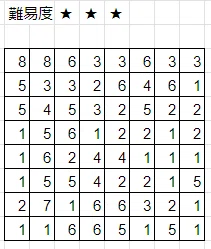
問題
これらの問題は、自動生成された問題です。様々なサイズの問題を自動生成することができます。
なお、難易度は自動ではなく、私の主観で付けています。
良ければ時間のある時にでも解いてみてください。
ChatGPT o1-mini をどう使ったのか
最初のプロンプト
最初に以下のプロンプトをChatGPT o1-miniに与えました。
4×4くらいの小さいグリッドサイズから楽しめる、マスを塗りつぶすタイプの新しいペンシルパズルのルールを考えてください。さらに、そのパズルの問題を作るpythonコードを書いてください。さらに、そのパズルの問題を解くpythonコードを作成し、解が一つしかないことを確認するようにしてください。解が一つになるまで、問題を修正するようにコーディングしてください。コードは、現実的な時間で実行できるように工夫してください。
ChatGPT o1の場合、プロンプトにすべての指示を盛り込むと、複数回のやり取りをせずに問題生成がスムーズに進むと思います。
また、直接パズル問題を生成させるのではなく、Pythonコードを生成させることがポイントです。Pythonコードを介することでルールに破綻のない問題を作成することができます。ただし、実行に時間がかかりすぎることや、コードにバグがあることはあるため、コード修正のための試行錯誤が必要です。
ChatGPTが提案してきた最初のルールは、以下のようなものでした。
「四方数字パズル」のルール
- グリッド: 正方形のグリッドがあります(例えば4×4)
- 数字マス: 一部のマスには数字が入っています。この数字は、そのマスの上下左右に隣接する黒マスの数を示しています
- 黒マスの配置:
- 黒マス同士は縦横に隣接してはいけません(斜めの隣接は可能です)
- 2×2の黒マスの塊を作ってはいけません
- 白マスの連結性: 黒く塗られていないマス(白マス)は、全てが一つの連続した領域になっていなければなりません
このように、それらしいルールを生成してくれます。ただし今回は生成されたルールをそのまま使わずに、いくつかのルールを採用しつつ、こちらでルールを確定しました。
次のルールでパズルを作れるか検討してください。
・ グリッド: 正方形のグリッドがあります(例えば4×4)。
・ 数字マス: すべてのマスには数字が入っています
・ 黒マスの配置: 黒マス同士は縦横に隣接してはいけません(斜めの隣接は可能です)。
・ 白マスの連結性: 黒く塗られていないマス(白マス)は、全てが一つの連続した領域になっていなければなりません。
・ 縦または横の方向で、黒マスと黒マスで挟まれた領域において、同じ数字は1度しか出現しない
ここからは、o1-miniと協働でコーディング作業を行っています。実現したい機能や手順を伝えてコードを生成させたり、エラーを伝えてコードを修正させたりするのにo1-miniを使っています。
機能や手順を伝えてコードを生成させる雰囲気をつかんでもらうため、こちらからのプロンプトを載せます。エラーコードを貼り付けての修正のためのやり取りは割愛します。
この方法で問題生成するのは大変そうです。次の手順に変更してください。
・ 制約を満たすように、黒マスをランダムに配置する。
・ 制約を満たすように、白マスの数字を埋める。
・白マスの数字の出現分布に合わせて、黒マスの数字をランダムに埋める。
黒マスが最初から分かっている前提で解の唯一性を確認しているようですが、実際には黒マスの位置は最初はわかっていません。
N=4での実行結果は大丈夫そうでした。しかし、N=5でも実行時間が長すぎます。落ち着いて考えてよいので、高速化について検討してください。Z3ソルバーなどのソルバーの利用も検討してください。
N=4でもものすごく時間がかかっています。 Z3ソルバーで一度に解くことが難しければ、緩和した問題を解き、緩和問題の解が制約を厳密に満たしているかを高速なヒューリスティックスで最終確認する、というアプローチも検討してください。
解の一意性をヒューリスティックに確認するというのはやめて、 緩和問題の解と全く同じ解はNGという制約を追加した緩和問題を解くことで、別の解を見つけるというループにしてください。
Z3ソルバーで、黒マスが縦横に連続しないという制約は追加してください。
generate_puzzleのなかで初期値のnumbersを生成するコードとして、次の手順でnumbersを生成するgenerate_numbers関数を作ってください。
・ 黒マスの隣接制約と白マスの連結制約を考慮してランダムに黒マスを生成できるだけ生成
・ 白マスの数字の制約を満たすように、白マスの数字を生成
・ 白マスの数字の出現頻度に応じた確率で、黒マスの数字を生成
assign_numbers_to_white_cells にて重複が起きています。 この関数内で、白マスの数字の制約を満たすように、Z3ソルバーで定式化して解くことはできますか?
Z3の緩和問題で、白マスの数字に関する制約を入れることはできますか?もう一度挑戦してみたいです。
白マスの数字に関する制約は以下の通りです。実装は異なっています。
縦または横の方向で、黒マスと黒マスで挟まれた領域において、同じ数字は1度しか出現しない
numbers[i][j] == 0 を黒マス (1) として扱い、それ以外を白マス (0) として扱うというのは誤りです。numbersでは黒マスか白マスかの判断は尽きません。cellsの情報を用いる必要があります。
6×6のサイズで、30~40秒程度かかりました。さらなる高速化はできますか?ゆっくり、深呼吸して慎重に検討してください。
(緩和問題なので)完ぺきではなくてもよいので、白マスの連結性の制約をZ3の定式化に取り込むことはできますか?
numbers[i][j] != 0 で最初の白マスを特定しようとしていますが、問題が与えられたとき、どのマスが白マスかはわかっていません。
各白マスが少なくとも一つの隣接する白マスと繋がっているという制約を書いてください。
コーディングでかなりのやり取りをしていることがわかると思います。そして、実はo1-miniの回答でうまくいかなかったものもあり、結構コードを自分で書いてます。複数解がでやすく、複数解がでたときのヒューリスティックスによる問題修正もそこまで賢くないので、最終的なコードでもかなり時間がかかります。8×8のサイズで問題を1問生成するのに平均15秒弱かかっています。
コードの解説
最初にChatGPTに依頼したのは、以下の3つの機能です。
- ルールを満たす解をもつ問題を生成する機能
- 問題が解を複数持つかどうかを判定する機能
- 問題が解を複数持つ場合に問題を微修正する機能
main
main関数は以下の通りで、グリッドサイズを指定し、generate_puzzle関数を呼び出します。この関数の中に、上記1,2,3の機能がすべて含まれています。
def main():
size = 4 # グリッドのサイズ
start_time = time.time()
numbers, solution = generate_puzzle(size)
end_time = time.time()
if solution:
print(f"\nパズルの生成に成功しました。(所要時間: {end_time - start_time:.2f}秒)")
print("\n生成されたパズル(数字グリッド):")
for i in range(size):
print(' '.join(str(numbers[i][j]) for j in range(size)))
print("\n解答(黒マスは1、白マスは0):")
for i in range(size):
print(' '.join(str(solution[i][j]) for j in range(size)))
else:
print("パズルの生成に失敗しました。")
generate_puzzle: 唯一解をもつパズルの生成
generate_puzzleの中身はこのようになっています。ここで、Z3というSMTソルバーを用いています。SMTはSatisfiability Modulo Theories(背景理論付き充足可能性問題)の略で、SATの拡張と捉えることができ、命題論理だけでなく、例えば算術理論(四則演算や不等号)などを扱うことができます。
from z3 import *
import random
import time
def generate_puzzle(size, max_attempts=100, verbose=True):
attempt = 0
solutions = []
grid = None
numbers = None
while attempt < max_attempts:
attempt += 1
if verbose:
print(f"試行回数: {attempt}")
grid, numbers = generate_numbers(size, solutions, grid, numbers)
if verbose:
print('初期問題を生成しました。')
s = None
solutions = []
# セルの状態を表す変数を定義(0: 白マス, 1: 黒マス)
cells = [[Int(f'cell_{i}_{j}') for j in range(size)] for i in range(size)]
while True:
# 1. 緩和問題を解く
s, solution = solve_relaxed_problem(numbers, solutions, size, s, cells)
if solution is None:
break # 解なしでループを抜ける
else:
# 2. 解を検証
if validate_solution(solution, numbers, size):
solutions.append(solution)
if len(solutions) > 1:
break # 複数解でループを抜ける
else:
# 制約を満たさない場合、再試行
continue
# ループ結果の確認
if len(solutions) == 0:
if verbose:
print("解なしでした。再試行します。")
print(numbers)
print(grid)
continue # 解なし、再試行
if len(solutions) == 1:
if verbose:
print("解が一意の問題が生成されました。")
return numbers, solutions[0]
else:
if verbose:
print("解が複数の問題が生成されました。再試行します。")
print(numbers)
print(grid)
print(solutions[0])
print(solutions[1])
continue # 解なし、再試行
return None, None
generate_numbers関数で正解と問題のペアを生成します。その後、while Trueのループの中で解を複数持つかのチェックを行い、解が一つであれば問題として出力しています。解が一つに定まらない場合、再度generate_numbers関数で問題を生成します。
# セルの状態を表す変数を定義(0: 白マス, 1: 黒マス)
cells = [[Int(f'cell_{i}_{j}') for j in range(size)] for i in range(size)]
ここで、IntはZ3からimportされた関数です。最適化対象となる、整数型の変数を返します。
generate_numbers: 初期問題の生成と問題の修正
次に、generate_numbers関数を見てみましょう。この関数は、初期問題の生成と、問題の修正の両方の機能を持っています。
以下の手順で初期問題を生成しています。
- 黒マスの場所を決める
- 白マスに適切な数字を割り当てる
- 黒マスに適当な数字を割り当てる
問題の修正は、以下のように行っています。
2つの解のうち、片方だけが黒マスとなっているマスを特定し、そのマスに隣接する白マスの数字で置き換える。(こうすることで、そのマスが白マスであるという解答はルール数字の制約を満たさなくなり、解の候補から落ちる)
def generate_numbers(size, solutions, grid=None, numbers=None):
if len(solutions) == 0:
max_attempts = 10 # 最大試行回数を設定
attempt = 0
while attempt < max_attempts:
attempt += 1
# 1. 黒マスの生成
grid = generate_black_cells(size)
# 2. 白マスの数字の割り当て
numbers = assign_numbers_to_white_cells(grid, size)
if numbers is not None:
# 3. 黒マスの数字の割り当て
numbers = assign_numbers_to_black_cells(grid, numbers, size)
return grid, numbers
# 最大試行回数を超えた場合は None を返す
return None, None
else:
max_attempts = 10 # 最大試行回数を設定
attempt = 0
while attempt < max_attempts:
attempt += 1
# solutions[0] と solutions[1] の比較
solution1 = solutions[0]
solution2 = solutions[1]
size = len(solution1)
# 条件を満たす座標をリストアップ
candidate_coords = []
for i in range(size):
for j in range(size):
if solution1[i][j] == 0 and solution2[i][j] == 1:
candidate_coords.append((i, j))
if not candidate_coords:
# 該当する座標がない場合、solution1と2を入れ替え
solution1, solution2 = solution2, solution1
for i in range(size):
for j in range(size):
if solution1[i][j] == 0 and solution2[i][j] == 1:
candidate_coords.append((i, j))
if not candidate_coords:
print('該当する座標がない。')
return None, None
# ランダムに1つの座標を選択
x, y = random.choice(candidate_coords)
# 選択した座標の上下左右の白マスを取得
adjacent_white_cells = []
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
nx, ny = x, y
while True:
nx, ny = nx + dx, ny + dy
if 0 <= nx < size and 0 <= ny < size:
if solution2[nx][ny] == 0:
if numbers[x][y] != numbers[nx][ny]: # 同じものを取ってきても仕方がない
adjacent_white_cells.append((nx, ny))
else:
break
else:
break
if not adjacent_white_cells:
# 隣接する白マスがない場合、再度パズルを生成
return None, None
# 隣接する白マスのいずれかから数字を取得
nx, ny = random.choice(adjacent_white_cells)
# numbers を更新(選択した座標の数字を隣接する白マスの数字にコピー)
numbers[x][y] = numbers[nx][ny]
return grid, numbers
# 最大試行回数を超えた場合は None を返す
return None, None
def generate_black_cells(size):
grid = [[0 for _ in range(size)] for _ in range(size)] # 0: 白マス, 1: 黒マス
positions = [(i, j) for i in range(size) for j in range(size)]
random.shuffle(positions)
for i, j in positions:
# 隣接する黒マスがないか確認
if has_adjacent_black_cell(grid, i, j, size):
continue
# 仮に黒マスを配置
grid[i][j] = 1
# 白マスの連結性を確認
if not is_white_connected(grid, size):
# 黒マスを取り消す
grid[i][j] = 0
return grid
def has_adjacent_black_cell(grid, i, j, size):
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
ni, nj = i + dx, j + dy
if 0 <= ni < size and 0 <= nj < size and grid[ni][nj] == 1:
return True
return False
def is_white_connected(grid, size):
visited = [[False]*size for _ in range(size)]
# 最初の白マスを探す
found = False
for i in range(size):
for j in range(size):
if grid[i][j]==0:
start = (i,j)
found = True
break
if found:
break
if not found:
return False # 白マスがない
# 深さ優先探索で連結性を確認
stack = [start]
visited[start[0]][start[1]] = True
while stack:
x, y = stack.pop()
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = x+dx, y+dy
if 0<=nx<size and 0<=ny<size and grid[nx][ny]==0 and not visited[nx][ny]:
visited[nx][ny] = True
stack.append((nx, ny))
# 全ての白マスに訪問できたか確認
for i in range(size):
for j in range(size):
if grid[i][j]==0 and not visited[i][j]:
return False
return True
def assign_numbers_to_white_cells(grid, size):
numbers = [[0 for _ in range(size)] for _ in range(size)]
s = Solver()
cells = [[Int(f'num_{i}_{j}') if grid[i][j] == 0 else None for j in range(size)] for i in range(size)]
# 1. セルの値の範囲制約を追加
for i in range(size):
for j in range(size):
if cells[i][j] is not None:
s.add(And(1 <= cells[i][j], cells[i][j] <= size))
# 2. 行ごとの重複禁止制約を追加
for i in range(size):
j = 0
while j < size:
# 黒マスをスキップ
while j < size and grid[i][j] == 1:
j += 1
seq_indices = []
while j < size and grid[i][j] == 0:
seq_indices.append(j)
j += 1
if seq_indices:
seq_vars = [cells[i][col] for col in seq_indices]
s.add(Distinct(seq_vars))
# 3. 列ごとの重複禁止制約を追加
for j in range(size):
i = 0
while i < size:
# 黒マスをスキップ
while i < size and grid[i][j] == 1:
i += 1
seq_indices = []
while i < size and grid[i][j] == 0:
seq_indices.append(i)
i += 1
if seq_indices:
seq_vars = [cells[row][j] for row in seq_indices]
s.add(Distinct(seq_vars))
# ソルバーを実行
if s.check() == sat:
m = s.model()
for i in range(size):
for j in range(size):
if grid[i][j] == 0:
numbers[i][j] = m.evaluate(cells[i][j]).as_long()
else:
# 解が見つからない場合は None を返す
return None
return numbers
def assign_numbers_to_black_cells(grid, numbers, size):
# 白マスの数字の出現頻度を計算
num_freq = {}
for i in range(size):
for j in range(size):
if grid[i][j] == 0:
num = numbers[i][j]
num_freq[num] = num_freq.get(num, 0) + 1
# 重み付きリストを作成
weighted_nums = []
for num, freq in num_freq.items():
weighted_nums.extend([num]*freq)
# 黒マスに数字を割り当て
for i in range(size):
for j in range(size):
if grid[i][j] == 1:
numbers[i][j] = random.choice(weighted_nums)
return numbers
assign_numbers_to_white_cells: Z3を用いた白マスへの数字の割り当て
さて、白マスにルールを満たすように適切な数字を割り当てるために、assign_numbers_to_white_cellsという関数の中でZ3を使っています。ここだけ改めて取り出して見てみましょう。
cellsが最適化対象の変数で、各白マスに入る数字です。
def assign_numbers_to_white_cells(grid, size):
numbers = [[0 for _ in range(size)] for _ in range(size)]
s = Solver()
cells = [[Int(f'num_{i}_{j}') if grid[i][j] == 0 else None for j in range(size)] for i in range(size)]
# 1. セルの値の範囲制約を追加
for i in range(size):
for j in range(size):
if cells[i][j] is not None:
s.add(And(1 <= cells[i][j], cells[i][j] <= size))
# 2. 行ごとの重複禁止制約を追加
for i in range(size):
j = 0
while j < size:
# 黒マスをスキップ
while j < size and grid[i][j] == 1:
j += 1
seq_indices = []
while j < size and grid[i][j] == 0:
seq_indices.append(j)
j += 1
if seq_indices:
seq_vars = [cells[i][col] for col in seq_indices]
s.add(Distinct(seq_vars))
# 3. 列ごとの重複禁止制約を追加
for j in range(size):
i = 0
while i < size:
# 黒マスをスキップ
while i < size and grid[i][j] == 1:
i += 1
seq_indices = []
while i < size and grid[i][j] == 0:
seq_indices.append(i)
i += 1
if seq_indices:
seq_vars = [cells[row][j] for row in seq_indices]
s.add(Distinct(seq_vars))
# ソルバーを実行
if s.check() == sat:
m = s.model()
for i in range(size):
for j in range(size):
if grid[i][j] == 0:
numbers[i][j] = m.evaluate(cells[i][j]).as_long()
else:
# 解が見つからない場合は None を返す
return None
return numbers
各白マスには1からグリッドサイズまでの整数値のいずれかが入ります。その制約は以下のように、不等式と、Andを用いて書くことができます。solverに、addメソッドを使って制約式を追加しています。
# 1. セルの値の範囲制約を追加
for i in range(size):
for j in range(size):
if cells[i][j] is not None:
s.add(And(1 <= cells[i][j], cells[i][j] <= size))
次に、ルールの数字の制約です。これは、行と列それぞれの方向について、外周または黒マスで囲まれる領域(コードのseq_indices)に対して、同じ数字がないという制約であり、Distinctを用いて書くことができます。生成されたコードをそのまま使っているので、ループがちょっと読みにくいですね。
# 2. 行ごとの重複禁止制約を追加
for i in range(size):
j = 0
while j < size:
# 黒マスをスキップ
while j < size and grid[i][j] == 1:
j += 1
seq_indices = []
while j < size and grid[i][j] == 0:
seq_indices.append(j)
j += 1
if seq_indices:
seq_vars = [cells[i][col] for col in seq_indices]
s.add(Distinct(seq_vars))
# 3. 列ごとの重複禁止制約を追加
for j in range(size):
i = 0
while i < size:
# 黒マスをスキップ
while i < size and grid[i][j] == 1:
i += 1
seq_indices = []
while i < size and grid[i][j] == 0:
seq_indices.append(i)
i += 1
if seq_indices:
seq_vars = [cells[row][j] for row in seq_indices]
s.add(Distinct(seq_vars))
これらの制約を満たす解をsolverで求めます。s.check()により、問題に解が存在するかどうかを判定します。存在する場合、その解の一つが得られるため、それを白マスの数字として採用します。
# ソルバーを実行
if s.check() == sat:
m = s.model()
for i in range(size):
for j in range(size):
if grid[i][j] == 0:
numbers[i][j] = m.evaluate(cells[i][j]).as_long()
else:
# 解が見つからない場合は None を返す
return None
generate_puzzle再見: 唯一解のチェックループ
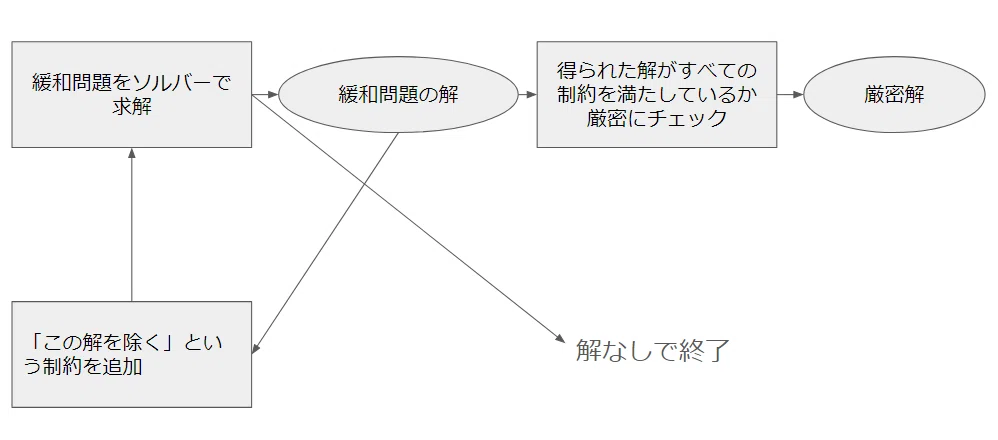
さて、これでルールを満たすような問題を生成することができるようになりました。しかし、パズルとして成立するためには、解が唯一解であり、他に解を持たない必要があります。そこで、生成された問題を改めて解き、解が一意であることを確認します。
ところが、ここでZ3での記述が非常に難しい制約が生じます。以下のルールです。
白マスの連結性:
黒く塗られていないマスを白マスと呼びます。すべての白マスは、縦横で連続した一つの領域になる必要があります。つまり、黒マスによって盤面が分断されてはいけません
この制約をZ3で記述することは難しいため、以下の緩和した制約を考え、この制約を満たす解を求めることにします。
白マスの連結性(緩和版):
黒く塗られていないマスを白マスと呼びます。すべての白マスは、縦横に少なくとも一つ、別の白マスと接している必要があります。
しかしそれでは本来のルールを満たさない解も得られてしまうため、Z3で得られた解が本来のルールも満たしているかどうか、後からチェックすることにします。
Z3ソルバーでは解が一つだけ得られます。複数解があるかどうかをチェックするためには、すでに得られた解は除くという制約を追加した問題を解けばよいです。
それではコードを見ていきましょう。
def generate_puzzle(size, max_attempts=100, verbose=True):
attempt = 0
solutions = []
grid = None
numbers = None
while attempt < max_attempts:
attempt += 1
if verbose:
print(f"試行回数: {attempt}")
grid, numbers = generate_numbers(size, solutions, grid, numbers)
if verbose:
print('初期問題を生成しました。')
s = None
solutions = []
# セルの状態を表す変数を定義(0: 白マス, 1: 黒マス)
cells = [[Int(f'cell_{i}_{j}') for j in range(size)] for i in range(size)]
while True:
# 1. 緩和問題を解く
s, solution = solve_relaxed_problem(numbers, solutions, size, s, cells)
if solution is None:
break # 解なしでループを抜ける
else:
# 2. 解を検証
if validate_solution(solution, numbers, size):
solutions.append(solution)
if len(solutions) > 1:
break # 複数解でループを抜ける
else:
# 制約を満たさない場合、再試行
continue
# ループ結果の確認
if len(solutions) == 0:
if verbose:
print("解なしでした。再試行します。")
print(numbers)
print(grid)
continue # 解なし、再試行
if len(solutions) == 1:
if verbose:
print("解が一意の問題が生成されました。")
return numbers, solutions[0]
else:
if verbose:
print("解が複数の問題が生成されました。再試行します。")
print(numbers)
print(grid)
print(solutions[0])
print(solutions[1])
continue # 解なし、再試行
return None, None
def solve_relaxed_problem(numbers, solutions, size, s=None, cells=None):
if s is None:
s = Solver()
# セルの状態は0か1
for i in range(size):
for j in range(size):
s.add(Or(cells[i][j] == 0, cells[i][j] == 1))
# 黒マスが縦横に隣接してはいけないという制約を追加
for i in range(size):
for j in range(size):
if i < size -1:
s.add(Implies(cells[i][j] == 1, cells[i+1][j] != 1))
if j < size -1:
s.add(Implies(cells[i][j] == 1, cells[i][j+1] != 1))
if i > 0:
s.add(Implies(cells[i][j] == 1, cells[i-1][j] != 1))
if j > 0:
s.add(Implies(cells[i][j] == 1, cells[i][j-1] != 1))
# 各白マスが少なくとも一つの隣接する白マスと繋がっているという制約を追加
add_adjacency_constraints(s, cells, size)
# 行ごとの数字の重複禁止制約を追加
for i in range(size):
for j in range(size-1):
for k in range(j+1, size):
seq_cells = [cells[i][a] == 0 for a in range(j, k+1)]
seq_nums = [IntVal(numbers[i][a]) for a in range(j, k+1)]
s.add(Implies(And(seq_cells), Distinct(seq_nums)))
# 列ごとの数字の重複禁止制約を追加
for j in range(size):
for i in range(size-1):
for k in range(i+1, size):
seq_cells = [cells[a][j] == 0 for a in range(i, k+1)]
seq_nums = [IntVal(numbers[a][j]) for a in range(i, k+1)]
s.add(Implies(And(seq_cells), Distinct(seq_nums)))
# 最初の解を見つける
if s.check() == sat:
m = s.model()
solution = [[m.evaluate(cells[i][j]).as_long() for j in range(size)] for i in range(size)]
# 既存の解を除外する制約を追加
s.add(Not(And([cells[i][j] == solution[i][j] for i in range(size) for j in range(size)])))
return s, solution
else:
return s, None # 解なし
def get_neighbors(i, j, size):
neighbors = []
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
ni, nj = i + dx, j + dy
if 0 <= ni < size and 0 <= nj < size:
neighbors.append((ni, nj))
return neighbors
def add_adjacency_constraints(s, cells, size):
"""
各白マスが少なくとも一つの隣接する白マスと繋がっているという制約を追加します。
Args:
s (Solver): Z3のソルバーインスタンス
cells (list of list of Int): 各セルの状態を表すZ3変数のリスト
size (int): グリッドのサイズ
"""
for i in range(size):
for j in range(size):
# セルが白マスである場合
is_white = cells[i][j] == 0
# 隣接する白マスの条件
adjacent_whites = []
for ni, nj in get_neighbors(i, j, size):
adjacent_whites.append(cells[ni][nj] == 0)
# 少なくとも一つの隣接セルが白マスである制約
if adjacent_whites:
s.add(Implies(is_white, Or(adjacent_whites)))
else:
# 隣接セルが存在しない(グリッドが1x1の場合など)
# その場合、セルが白マスであれば制約を満たさない
# つまり、セルが白マスであれば矛盾を生じさせる
s.add(Implies(is_white, False))
def validate_solution(solution, numbers, size):
# 1. 黒マスが縦横に隣接していないか確認
for i in range(size):
for j in range(size):
if solution[i][j] == 1:
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
ni, nj = i + dx, j + dy
if 0 <= ni < size and 0 <= nj < size and solution[ni][nj] == 1:
return False
# 2. 白マスの連結性を確認
if not check_white_connected(solution, size):
return False
# 3. 数字の重複禁止を確認
# 行ごとに確認
for i in range(size):
idx = 0
while idx < size:
while idx < size and solution[i][idx] == 1:
idx += 1
seq_numbers = []
while idx < size and solution[i][idx] == 0:
seq_numbers.append(numbers[i][idx])
idx += 1
if len(seq_numbers) != len(set(seq_numbers)):
return False
# 列ごとに確認
for j in range(size):
idx = 0
while idx < size:
while idx < size and solution[idx][j] == 1:
idx += 1
seq_numbers = []
while idx < size and solution[idx][j] == 0:
seq_numbers.append(numbers[idx][j])
idx += 1
if len(seq_numbers) != len(set(seq_numbers)):
return False
return True
def check_white_connected(grid, size):
visited = [[False]*size for _ in range(size)]
# 最初の白マスを探す
found = False
for i in range(size):
for j in range(size):
if grid[i][j]==0:
start = (i,j)
found = True
break
if found:
break
if not found:
return False # 白マスがない
# 深さ優先探索で連結性を確認
stack = [start]
visited[start[0]][start[1]] = True
while stack:
x, y = stack.pop()
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = x+dx, y+dy
if 0<=nx<size and 0<=ny<size and grid[nx][ny]==0 and not visited[nx][ny]:
visited[nx][ny] = True
stack.append((nx, ny))
# 全ての白マスに訪問できたか確認
for i in range(size):
for j in range(size):
if grid[i][j]==0 and not visited[i][j]:
return False
return True
solve_relaxed_problem: Z3による緩和問題の求解
solve_relaxed_problem関数の中で、Z3のオペレーションとしてあらたにOr, Implies(ならば)も使って定式化しています。
一つ一つ、制約の書き方を見てみましょう。
# セルの状態は0か1
for i in range(size):
for j in range(size):
s.add(Or(cells[i][j] == 0, cells[i][j] == 1))
まず、セルの状態は1(黒)か0(白)のどちらかという制約を、Orを使って表現しています。
# 黒マスが縦横に隣接してはいけないという制約を追加
for i in range(size):
for j in range(size):
if i < size -1:
s.add(Implies(cells[i][j] == 1, cells[i+1][j] != 1))
if j < size -1:
s.add(Implies(cells[i][j] == 1, cells[i][j+1] != 1))
if i > 0:
s.add(Implies(cells[i][j] == 1, cells[i-1][j] != 1))
if j > 0:
s.add(Implies(cells[i][j] == 1, cells[i][j-1] != 1))
つぎに、黒マスは縦横に隣接しないという制約です。あるセルが黒マスならば隣接するマスは黒マスではないというように、Implies(ならば)を使って書くことができます。
# 各白マスが少なくとも一つの隣接する白マスと繋がっているという制約を追加
for i in range(size):
for j in range(size):
# セルが白マスである場合
is_white = cells[i][j] == 0
# 隣接する白マスの条件
adjacent_whites = []
for ni, nj in get_neighbors(i, j, size):
adjacent_whites.append(cells[ni][nj] == 0)
# 少なくとも一つの隣接セルが白マスである制約
if adjacent_whites:
s.add(Implies(is_white, Or(adjacent_whites)))
else:
# 隣接セルが存在しない(グリッドが1x1の場合など)
# その場合、セルが白マスであれば制約を満たさない
# つまり、セルが白マスであれば矛盾を生じさせる
s.add(Implies(is_white, False))
各白マスが少なくとも一つの隣接する白マスと繋がっているという制約です。隣接するマスの中に少なくとも一つ白マスがあるというのは、Orで書くことができます。あるセルが白マスならばという制約なので、ここでもImpliesを使います。
# 行ごとの数字の重複禁止制約を追加
for i in range(size):
for j in range(size-1):
for k in range(j+1, size):
seq_cells = [cells[i][a] == 0 for a in range(j, k+1)]
seq_nums = [IntVal(numbers[i][a]) for a in range(j, k+1)]
s.add(Implies(And(seq_cells), Distinct(seq_nums)))
外周または黒マスで区切られた縦横の領域に同じ数字が出現しないという制約です。同じ数字が出現しないという制約はDistinctで書くことができます。ここでは、どこが黒マスになるかわからないので、連続するマスの組み合わせを全て列挙して、すべての組み合わせに対して「連続するマスがすべて白マスならば、そのマスに同じ数字が出現しない」という書き方をしているので、AndとImpliesが使われています。IntValは整数値をZ3で扱うための関数です。
コードの完全版
最後に、一連のコードを改めて一つにまとめたものを載せておきます。
from z3 import *
import random
import time
def generate_puzzle(size, max_attempts=100, verbose=True):
attempt = 0
solutions = []
grid = None
numbers = None
while attempt < max_attempts:
attempt += 1
if verbose:
print(f"試行回数: {attempt}")
grid, numbers = generate_numbers(size, solutions, grid, numbers)
if verbose:
print('初期問題を生成しました。')
s = None
solutions = []
# セルの状態を表す変数を定義(0: 白マス, 1: 黒マス)
cells = [[Int(f'cell_{i}_{j}') for j in range(size)] for i in range(size)]
while True:
# 1. 緩和問題を解く
s, solution = solve_relaxed_problem(numbers, solutions, size, s, cells)
if solution is None:
break # 解なしでループを抜ける
else:
# 2. 解を検証
if validate_solution(solution, numbers, size):
solutions.append(solution)
if len(solutions) > 1:
break # 複数解でループを抜ける
else:
# 制約を満たさない場合、再試行
continue
# ループ結果の確認
if len(solutions) == 0:
if verbose:
print("解なしでした。再試行します。")
print(numbers)
print(grid)
continue # 解なし、再試行
if len(solutions) == 1:
if verbose:
print("解が一意の問題が生成されました。")
return numbers, solutions[0]
else:
if verbose:
print("解が複数の問題が生成されました。再試行します。")
print(numbers)
print(grid)
print(solutions[0])
print(solutions[1])
continue # 解なし、再試行
return None, None
def generate_black_cells(size):
grid = [[0 for _ in range(size)] for _ in range(size)] # 0: 白マス, 1: 黒マス
positions = [(i, j) for i in range(size) for j in range(size)]
random.shuffle(positions)
for i, j in positions:
# 隣接する黒マスがないか確認
if has_adjacent_black_cell(grid, i, j, size):
continue
# 仮に黒マスを配置
grid[i][j] = 1
# 白マスの連結性を確認
if not is_white_connected(grid, size):
# 黒マスを取り消す
grid[i][j] = 0
return grid
def has_adjacent_black_cell(grid, i, j, size):
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
ni, nj = i + dx, j + dy
if 0 <= ni < size and 0 <= nj < size and grid[ni][nj] == 1:
return True
return False
def is_white_connected(grid, size):
visited = [[False]*size for _ in range(size)]
# 最初の白マスを探す
found = False
for i in range(size):
for j in range(size):
if grid[i][j]==0:
start = (i,j)
found = True
break
if found:
break
if not found:
return False # 白マスがない
# 深さ優先探索で連結性を確認
stack = [start]
visited[start[0]][start[1]] = True
while stack:
x, y = stack.pop()
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = x+dx, y+dy
if 0<=nx<size and 0<=ny<size and grid[nx][ny]==0 and not visited[nx][ny]:
visited[nx][ny] = True
stack.append((nx, ny))
# 全ての白マスに訪問できたか確認
for i in range(size):
for j in range(size):
if grid[i][j]==0 and not visited[i][j]:
return False
return True
def assign_numbers_to_white_cells(grid, size):
numbers = [[0 for _ in range(size)] for _ in range(size)]
s = Solver()
cells = [[Int(f'num_{i}_{j}') if grid[i][j] == 0 else None for j in range(size)] for i in range(size)]
# 1. セルの値の範囲制約を追加
for i in range(size):
for j in range(size):
if cells[i][j] is not None:
s.add(And(1 <= cells[i][j], cells[i][j] <= size))
# 2. 行ごとの重複禁止制約を追加
for i in range(size):
j = 0
while j < size:
# 黒マスをスキップ
while j < size and grid[i][j] == 1:
j += 1
seq_indices = []
while j < size and grid[i][j] == 0:
seq_indices.append(j)
j += 1
if seq_indices:
seq_vars = [cells[i][col] for col in seq_indices]
s.add(Distinct(seq_vars))
# 3. 列ごとの重複禁止制約を追加
for j in range(size):
i = 0
while i < size:
# 黒マスをスキップ
while i < size and grid[i][j] == 1:
i += 1
seq_indices = []
while i < size and grid[i][j] == 0:
seq_indices.append(i)
i += 1
if seq_indices:
seq_vars = [cells[row][j] for row in seq_indices]
s.add(Distinct(seq_vars))
# ソルバーを実行
if s.check() == sat:
m = s.model()
for i in range(size):
for j in range(size):
if grid[i][j] == 0:
numbers[i][j] = m.evaluate(cells[i][j]).as_long()
else:
# 解が見つからない場合は None を返す
return None
return numbers
def assign_numbers_to_black_cells(grid, numbers, size):
# 白マスの数字の出現頻度を計算
num_freq = {}
for i in range(size):
for j in range(size):
if grid[i][j] == 0:
num = numbers[i][j]
num_freq[num] = num_freq.get(num, 0) + 1
# 重み付きリストを作成
weighted_nums = []
for num, freq in num_freq.items():
weighted_nums.extend([num]*freq)
# 黒マスに数字を割り当て
for i in range(size):
for j in range(size):
if grid[i][j] == 1:
numbers[i][j] = random.choice(weighted_nums)
return numbers
def generate_numbers(size, solutions, grid=None, numbers=None):
if len(solutions) == 0:
max_attempts = 10 # 最大試行回数を設定
attempt = 0
while attempt < max_attempts:
attempt += 1
# 1. 黒マスの生成
grid = generate_black_cells(size)
# 2. 白マスの数字の割り当て
numbers = assign_numbers_to_white_cells(grid, size)
if numbers is not None:
# 3. 黒マスの数字の割り当て
numbers = assign_numbers_to_black_cells(grid, numbers, size)
return grid, numbers
# 最大試行回数を超えた場合は None を返す
return None, None
else:
max_attempts = 10 # 最大試行回数を設定
attempt = 0
while attempt < max_attempts:
attempt += 1
# solutions[0] と solutions[1] の比較
solution1 = solutions[0]
solution2 = solutions[1]
size = len(solution1)
# 条件を満たす座標をリストアップ
candidate_coords = []
for i in range(size):
for j in range(size):
if solution1[i][j] == 0 and solution2[i][j] == 1:
candidate_coords.append((i, j))
if not candidate_coords:
# 該当する座標がない場合、solution1と2を入れ替え
solution1, solution2 = solution2, solution1
for i in range(size):
for j in range(size):
if solution1[i][j] == 0 and solution2[i][j] == 1:
candidate_coords.append((i, j))
if not candidate_coords:
print('該当する座標がない。')
return None, None
# ランダムに1つの座標を選択
x, y = random.choice(candidate_coords)
# 選択した座標の上下左右の白マスを取得
adjacent_white_cells = []
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
nx, ny = x, y
while True:
nx, ny = nx + dx, ny + dy
if 0 <= nx < size and 0 <= ny < size:
if solution2[nx][ny] == 0:
if numbers[x][y] != numbers[nx][ny]: # 同じものを取ってきても仕方がない
adjacent_white_cells.append((nx, ny))
else:
break
else:
break
if not adjacent_white_cells:
# 隣接する白マスがない場合、再度パズルを生成
return None, None
# 隣接する白マスのいずれかから数字を取得
nx, ny = random.choice(adjacent_white_cells)
# numbers を更新(選択した座標の数字を隣接する白マスの数字にコピー)
numbers[x][y] = numbers[nx][ny]
return grid, numbers
# 最大試行回数を超えた場合は None を返す
return None, None
def solve_relaxed_problem(numbers, solutions, size, s=None, cells=None):
if s is None:
s = Solver()
# セルの状態は0か1
for i in range(size):
for j in range(size):
s.add(Or(cells[i][j] == 0, cells[i][j] == 1))
# 黒マスが縦横に隣接してはいけないという制約を追加
for i in range(size):
for j in range(size):
if i < size -1:
s.add(Implies(cells[i][j] == 1, cells[i+1][j] != 1))
if j < size -1:
s.add(Implies(cells[i][j] == 1, cells[i][j+1] != 1))
if i > 0:
s.add(Implies(cells[i][j] == 1, cells[i-1][j] != 1))
if j > 0:
s.add(Implies(cells[i][j] == 1, cells[i][j-1] != 1))
# 各白マスが少なくとも一つの隣接する白マスと繋がっているという制約を追加
add_adjacency_constraints(s, cells, size)
# 行ごとの数字の重複禁止制約を追加
for i in range(size):
for j in range(size-1):
for k in range(j+1, size):
seq_cells = [cells[i][a] == 0 for a in range(j, k+1)]
seq_nums = [IntVal(numbers[i][a]) for a in range(j, k+1)]
s.add(Implies(And(seq_cells), Distinct(seq_nums)))
# 列ごとの数字の重複禁止制約を追加
for j in range(size):
for i in range(size-1):
for k in range(i+1, size):
seq_cells = [cells[a][j] == 0 for a in range(i, k+1)]
seq_nums = [IntVal(numbers[a][j]) for a in range(i, k+1)]
s.add(Implies(And(seq_cells), Distinct(seq_nums)))
# 最初の解を見つける
if s.check() == sat:
m = s.model()
solution = [[m.evaluate(cells[i][j]).as_long() for j in range(size)] for i in range(size)]
# 既存の解を除外する制約を追加
s.add(Not(And([cells[i][j] == solution[i][j] for i in range(size) for j in range(size)])))
return s, solution
else:
return s, None # 解なし
def get_neighbors(i, j, size):
neighbors = []
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
ni, nj = i + dx, j + dy
if 0 <= ni < size and 0 <= nj < size:
neighbors.append((ni, nj))
return neighbors
def add_adjacency_constraints(s, cells, size):
"""
各白マスが少なくとも一つの隣接する白マスと繋がっているという制約を追加します。
Args:
s (Solver): Z3のソルバーインスタンス
cells (list of list of Int): 各セルの状態を表すZ3変数のリスト
size (int): グリッドのサイズ
"""
for i in range(size):
for j in range(size):
# セルが白マスである場合
is_white = cells[i][j] == 0
# 隣接する白マスの条件
adjacent_whites = []
for ni, nj in get_neighbors(i, j, size):
adjacent_whites.append(cells[ni][nj] == 0)
# 少なくとも一つの隣接セルが白マスである制約
if adjacent_whites:
s.add(Implies(is_white, Or(adjacent_whites)))
else:
# 隣接セルが存在しない(グリッドが1x1の場合など)
# その場合、セルが白マスであれば制約を満たさない
# つまり、セルが白マスであれば矛盾を生じさせる
s.add(Implies(is_white, False))
def validate_solution(solution, numbers, size):
# 1. 黒マスが縦横に隣接していないか確認
for i in range(size):
for j in range(size):
if solution[i][j] == 1:
for dx, dy in [(-1, 0), (1, 0), (0, -1), (0, 1)]:
ni, nj = i + dx, j + dy
if 0 <= ni < size and 0 <= nj < size and solution[ni][nj] == 1:
return False
# 2. 白マスの連結性を確認
if not check_white_connected(solution, size):
return False
# 3. 数字の重複禁止を確認
# 行ごとに確認
for i in range(size):
idx = 0
while idx < size:
while idx < size and solution[i][idx] == 1:
idx += 1
seq_numbers = []
while idx < size and solution[i][idx] == 0:
seq_numbers.append(numbers[i][idx])
idx += 1
if len(seq_numbers) != len(set(seq_numbers)):
return False
# 列ごとに確認
for j in range(size):
idx = 0
while idx < size:
while idx < size and solution[idx][j] == 1:
idx += 1
seq_numbers = []
while idx < size and solution[idx][j] == 0:
seq_numbers.append(numbers[idx][j])
idx += 1
if len(seq_numbers) != len(set(seq_numbers)):
return False
return True
def check_white_connected(grid, size):
visited = [[False]*size for _ in range(size)]
# 最初の白マスを探す
found = False
for i in range(size):
for j in range(size):
if grid[i][j]==0:
start = (i,j)
found = True
break
if found:
break
if not found:
return False # 白マスがない
# 深さ優先探索で連結性を確認
stack = [start]
visited[start[0]][start[1]] = True
while stack:
x, y = stack.pop()
for dx, dy in [(-1,0),(1,0),(0,-1),(0,1)]:
nx, ny = x+dx, y+dy
if 0<=nx<size and 0<=ny<size and grid[nx][ny]==0 and not visited[nx][ny]:
visited[nx][ny] = True
stack.append((nx, ny))
# 全ての白マスに訪問できたか確認
for i in range(size):
for j in range(size):
if grid[i][j]==0 and not visited[i][j]:
return False
return True
def main():
size = 4 # グリッドのサイズ
start_time = time.time()
numbers, solution = generate_puzzle(size)
end_time = time.time()
if solution:
print(f"\nパズルの生成に成功しました。(所要時間: {end_time - start_time:.2f}秒)")
print("\n生成されたパズル(数字グリッド):")
for i in range(size):
print(' '.join(str(numbers[i][j]) for j in range(size)))
print("\n解答(黒マスは1、白マスは0):")
for i in range(size):
print(' '.join(str(solution[i][j]) for j in range(size)))
else:
print("パズルの生成に失敗しました。")
if __name__ == "__main__":
main()
人間の関与を振り返る
今回のパズル製作において私の関与について振り返ってみます。
面白そうなルールの作成
生成AIからはルールが生成されますが、面白いルールかどうかは別です。面白いルールの選別や、面白いルールへの修正は人間の関与が必要です。
難易度の判定
問題は自動生成できますが、人にとっての難易度を自動で判定するのは少し難しそうです。ただ、人と同じようなロジックで解くプログラムを書ければ(あるいは、人と同じようなロジックで解くAIを学習できれば)難易度の自動判定もできそうなので、現状の技術でもがんばれば実現できるかもしれません。
問題生成手順の設計
現実的な時間で問題を生成するための手順を設計してあげないと、一発では良いコードが得られませんでした。
コードの修正
Z3のようなライブラリを用いたコードも概ね正しく書いてくれますが、一部はうまくいかず私が書きました。
まとめ
今回のように少し複雑なプログラムになってくると、まだ人間の設計が重要になりそうです。さらに、コードの一部を修正したり書いたりすることも必要そうです。来年にはこのくらい複雑なプログラムも私よりもっと良い設計ができるくらいに進化していると良いですね。
一方で、面白さの理解は来年でもまだ難しそうです。
生成AIと人間のコラボレーションで可能性を広げるためには、まだまだ、人間のセンスは重要ですし、プログラミング能力も重要そうですね。