台形則による定積分

高校数学で学ぶ台形則による定積分について書きます。
プログラミングは好き・出来るのに数学に苦手意識を持ってしまっている不幸な高校生が一人でも減る事を願っています。

そもそも定積分とは？

以下より丁寧に説明出来る気がしないので、ベネッセを紹介します。
https://kou.benesse.co.jp/nigate/math/a14m1402.html

積分する事によって面積が求められるんだよというお話。
積分を素直に実現するプログラムを書くのも良いですが、本記事では台形則と呼ばれる方法で定積分を行う方法を紹介します。

台形則による定積分の求め方

Wikiに詳しく書かれているので、キャプチャの紹介のみとします。
https://ja.wikipedia.org/wiki/%E5%8F%B0%E5%BD%A2%E5%85%AC%E5%BC%8F

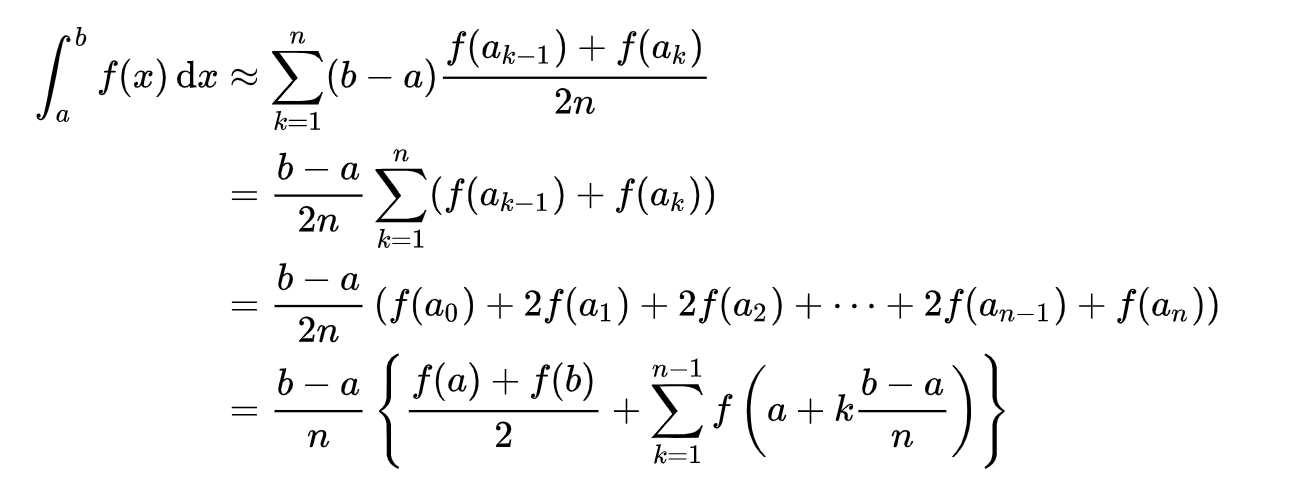
暗号みたいですが、図形で書くとイメージが出来ます

出典：https://nekodamashi-math.blog.ss-blog.jp/2016-11-14

被積分関数に対し、等間隔で点を打ち複数の台形を作ります。
その台形の合計値を求める事により定積分を実現しているという訳です。
それでは実際にコードに参りましょう。

C#による実装

Trapezoidal.cs

        public void Trapezoidal(double a, double b)
        {
            var bunkatsuNum = 50;
            var haba = (b - a) / bunkatsuNum;
            var x = a;
            double sum = 0;

            for(int k=1;k<=bunkatsuNum-1;k++)
            {
                x = x + haba;
                sum = sum + targetFunction(x);
            }

            sum = haba * ((targetFunction(a) + targetFunction(b)) / 2 + sum);
            Console.WriteLine(sum);
        }

        private double targetFunction(double x)
        {
            return x * 2 + 2;
        }

taegetFunctionの中身を積分したい式にしてくれれば良いです。
今回の例は、要するに
2X + 2であり、積分するとx^2 + 2xになります。

実際に動かして見ると、ちゃんと定積分出来ます。
今後も同様の記事を書き続けるので、頑張って数学嫌いを克服していきましょう!!