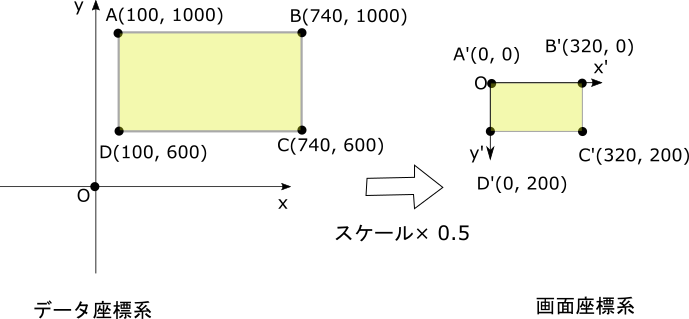本記事はJavaFX Advent Calendar 2016の12日目です。昨日は、@skrbさんのScene Builder 小ネタ 3つです。明日は、@sk44_さんです。
はじめに
JavaFXのCanvasには、線、矩形、楕円、ポリゴンなどのベクトルデータや画像データを描画する2Dグラフィックス機能があります。また、アフィン変換を指定して、拡大、縮小、平行移動、回転、せん断といった2D描画の変形が可能です。
ここで、画面よりも大きな2Dデータを、任意に拡大、縮小して表示する、上下左右にスクロールして表示する、という操作をアフィン変換を使って実現するとします。地図の表示、CADデータの表示、などが一例です。
アフィン変換は、原理はシンプルなように見えますが、やってみるとはまることが多く、2年前にもCanvasでAffine変換で大いにはまる(数学的センスが足りなかった・・・)というブログを書いたほどです。
今月3日に開催されたJJUG CCC 2016 Fallにおいて、「世界は四角ではない~JavaFXで地図を描く」という題目で、地図データ(世界海岸線データ)をJavaFXのCanvasで描画する内容を発表しました。このときに用意した地図表示サンプルプログラムでは、アフィン変換を使って拡大・縮小・スクロールを行っています。ですが、拡大・縮小をすると表示している地図の位置がずれてしまうという問題を抱えていました。残念ながら発表当日までには解決できませんでした。
そこで、リベンジとして、表示の拡大・縮小をするときは、画面に表示しているデータの中心がずれないように、アフィン変換を再度基礎から勉強し直し、整理してまとめることとしました。
本記事の実行環境
本記事は、JavaFXのアフィン変換を調べて理解することを目的に記述しているので、サンプルプログラムはありません。Affine変換の動作を簡単に確認するために、来年リリースされる予定のJDK 9に搭載されるコマンドライン環境jshellを使っています。
Windows 10 64bit環境の上で、Java SE Development Kit 9 Early Access版を入れてshellコマンドを使用しています。記事執筆時点では、JDK 9 Build 148バージョンです。
データ座標系と画面座標系
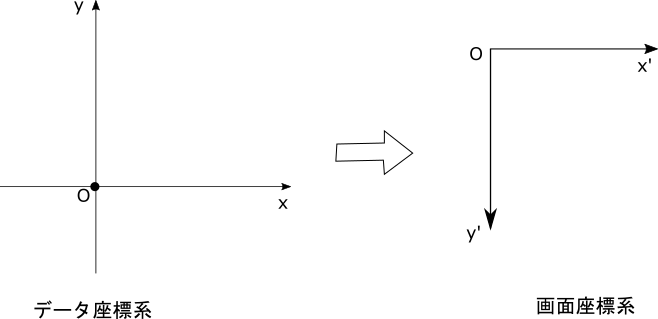
一般にデータの形状は、直交座標系で定義します。この直交座標系は右手系、つまりx軸の正の方向を反時計回りに90度回転した向きをy軸の正の方向として表します。
一方、JavaFXの画面座標も直交座標系で定義しますが、この直交座標系は左手系、つまりx軸の正の方向を時計回りに90度回転した向きをy軸の正の方向として表します。
そのため、データの座標をそのまま画面に表示すると上下が逆さまになってしまいます。
地図データを変換せずに表示すると・・・
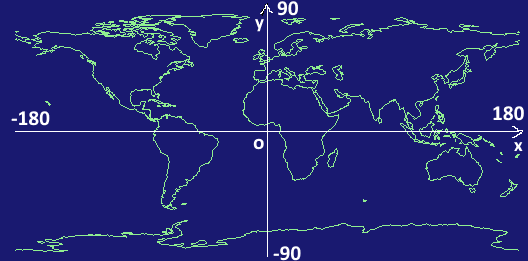
一般に地図データは、緯度経度座標で定義されています。これを、緯度をy軸、経度をx軸で表現すると、次のようなデータとなります。
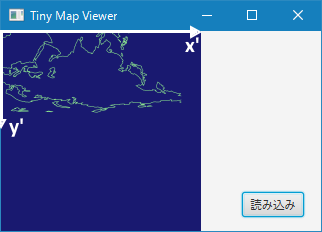
この地図データを、座標の変換を一切せずに画面に表示すると次のような表示となります。
地図データの座標系の第1象限(0,0)~(180,90)の範囲が上下逆さまで表示されています。
そこで、データ座標系から画面座標系への座標変換を導入して、データを任意に拡大・縮小・平行移動・回転して表示できるようにします。その際に使われる座標変換がアフィン変換となります。
アフィン変換によるデータ座標系から画面座標系への変換
データ座標系をxy座標系、画面座標系をx'y'座標系とします。
xy座標系上の点を(x, y)、x'y'座標系上の点を(x', y')とすると、データ座標系から画面座標系への座標変換は、(x, y)を入力として(x', y')を出力とする変換式となります。
x' = ax + by + t_x\\
y' = cx + dy + t_y
この変換式を、座標をベクトル、変換を行列で表現し直すと
\begin{pmatrix}
x'\\
y'\\
1
\end{pmatrix}
= \begin{pmatrix}
a & b & t_x\\
c & d & t_y\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\
y\\
1
\end{pmatrix}
となります。この行列がAffine変換行列となります。(2次元の場合)
計算の取り扱い上、3次のベクトル・行列で計算(同次座標)しています。
座標変換(その1):恒等変換
x' = x\\
y' = y\\
となる変換(つまり何も変換しない)を適用すると、上下逆さまの表示となります。アフィン変換で表現すると次となります。
\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}
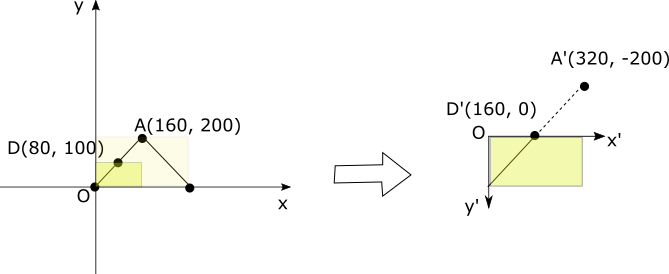
この変換(無変換)では、データは次のように画面に表示されます。
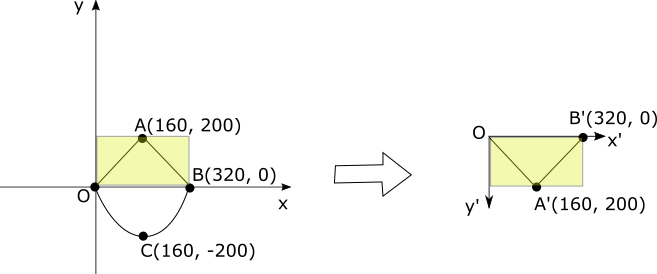
黄色い矩形部分が画面描画領域です。点A、B、Cは次のようにA', B', C'に変換(無変換)されます。
\begin{align*}
(A'_x, A'_y) &= (A_x, A_y) = (160, 200)\\
(B'_x, B'_y) &= (B_x, B_y) = (320, 0)\\
(C'_x, C'_y) &= (C_x, C_y) = (160, -200)
\end{align*}
このアフィン変換は、次のコードで作成されます。
Affine affine = new Affine();
JDK 9のjshell環境でAffineの実験
JDK 9に環境変数PATHを通しておきます。jshellを実行します。
C:\>java -version
java version "9-ea"
Java(TM) SE Runtime Environment (build 9-ea+148)
Java HotSpot(TM) 64-Bit Server VM (build 9-ea+148, mixed mode)
C:\>jshell
| JShellへようこそ -- バージョン9-ea
| 概要については、次を入力してください: /help intro
|
jshell>
Affine変換(恒等変換)を生成します。
jshell> import javafx.scene.transform.Affine
jshell> Affine affine = new Affine()
affine ==> Affine [
1.0, 0.0, 0.0, 0.0
0.0, 1.0, 0.0, 0.0
0.0, 0.0, 1.0, 0.0
]
jshell環境は、定義した変数の内容が表示されるので便利です。しかし、3行4列で表示されていますね。これは、JavaFX が標準で3Dグラフィックスを備えているので、3次元座標の変換に対応できるようになっています。
2Dのアフィン変換を扱う場合は、上図のように、3列目は気にしないでおきます。
次に、データ座標系の点を1つ作成し、このAffineで変換してみましょう。
jshell> import javafx.geometry.Point2D
jshell> Point2D dataA = new Point2D(160, 200)
dataA ==> Point2D [x = 160.0, y = 200.0]
jshell> affine.transform(dataA)
$5 ==> Point2D [x = 160.0, y = 200.0]
jshell>
元の座標(160,200)と同じ値の座標がこのAffineの変換結果として得られました。
座標変換(その2):上下逆さまの解消
y軸が逆になっているので、単純にはy座標の符号を逆にすればよいと考え次の座標変換を導入します。
\begin{align*}
x' &= x\\
y' &= -y\\
\end{align*}
アフィン変換で表現すると次となります。
\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}
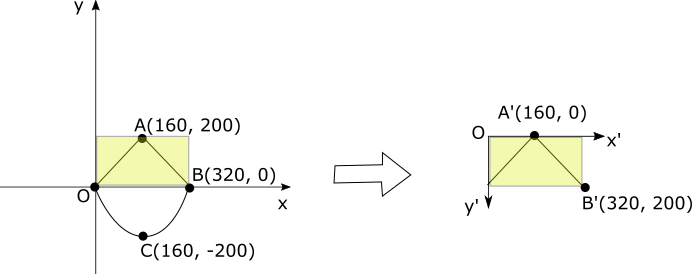
点A、B、Cは次のようにA', B', C'に変換されます。
\begin{align*}
(A'_x, A'_y) &= (A_x, -A_y) = (160, -200)\\
(B'_x, B'_y) &= (B_x, -B_y) = (320, 0)\\
(C'_x, C'_y) &= (C_x, -C_y) = (160, 200)
\end{align*}
データの表示が逆さまになることは解消されましたが、データの表示領域が(その1)での表示領域とはずれて(X軸の反対側)しまっています。
このアフィン変換は、次のコードで作成されます。
Affine affine = new Affine(1, 0, 0, 0, -1, 0);
JDK 9のjshell環境でAffineの実験
jshell> affine = new Affine(1, 0, 0, 0, -1, 0)
affine ==> Affine [
1.0, 0.0, 0.0, 0.0
0.0, -1.0, 0.0, 0.0
0.0, 0.0, 1.0, 0.0
]
jshell> affine.transform(dataA)
$9 ==> Point2D [x = 160.0, y = -200.0]
jshell>
点Aが(160, 200)から(160, -200)に変換されました。同様に点B、点Cについても変換結果を見てみましょう。
jshell> Point2D dataB = new Point2D(320, 0)
dataB ==> Point2D [x = 320.0, y = 0.0]
jshell> affine.transform(dataB)
$12 ==> Point2D [x = 320.0, y = -0.0]
jshell> Point2D dataC = new Point2D(160, -200)
dataC ==> Point2D [x = 160.0, y = -200.0]
jshell> affine.transform(dataC)
$13 ==> Point2D [x = 160.0, y = 200.0]
jshell>
点Bが(320, 0)から(320, -0)へ変換(座標値変化せず)されました。
点Cが(160, -200)から(160, 200)へ変換されました。
座標変換(その3):原点の平行移動
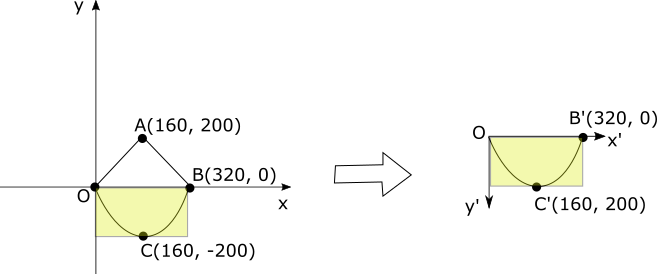
データ座標系の原点は描画したい領域の左下隅ですが、画面座標系の原点は描画される領域の左上隅となります。そこで、データ座標系の原点を画面座標系の原点へ平行移動させて描画したい領域を合わせます。
この場合の平行移動は、y軸方向に描画領域の高さ分の移動となります。描画領域の高さをhとすると次の変換式となります。
\begin{align*}
x' &= x\\
y' &= -(y - h) = -y + h\\
\end{align*}
アフィン変換で表現すると次となります。
\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & h\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}
高さhを200としたときの図と各座標は次となります。
\begin{align*}
(A'_x, A'_y) &= (A_x, -A_y + 200) = (160, 0)\\
(B'_x, B'_y) &= (B_x, -B_y + 200) = (320, 200)\\
(C'_x, C'_y) &= (C_x, -C_y + 200) = (160, 0)
\end{align*}
このアフィン変換は、次のコードで作成されます。
Affine affine = new Affine(1, 0, 0, 0, -1, 200);
JDK 9のjshell環境でAffineの実験
jshell> affine = new Affine(1, 0, 0, 0, -1, 200)
affine ==> Affine [
1.0, 0.0, 0.0, 0.0
0.0, -1.0, 0.0, 200.0
0.0, 0.0, 1.0, 0.0
]
jshell> affine.transform(dataA)
$19 ==> Point2D [x = 160.0, y = 0.0]
jshell> affine.transform(dataB)
$20 ==> Point2D [x = 320.0, y = 200.0]
jshell> affine.transform(dataC)
$21 ==> Point2D [x = 160.0, y = 400.0]
jshell>
点Aが(160, 200)から(160, 0)へ変換されました。
点Bが(320, 0)から(320, 200)へ変換されました。
点Cが(160, -200)から(160, 400)へ変換されました。
座標変換(その4):描画領域を移動
描画領域をデータ座標系の任意の箇所に移動させます。
描画領域の左上隅の座標を(x1, y1)とすると、次の式で平行移動を表します。
\begin{align*}
x' &= x - x_1\\
y' &= -(y - y_1) = -y + y_1
\end{align*}
アフィン変換で表現すると次となります。
\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & -x_1\\
0 & -1 & y_1\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}
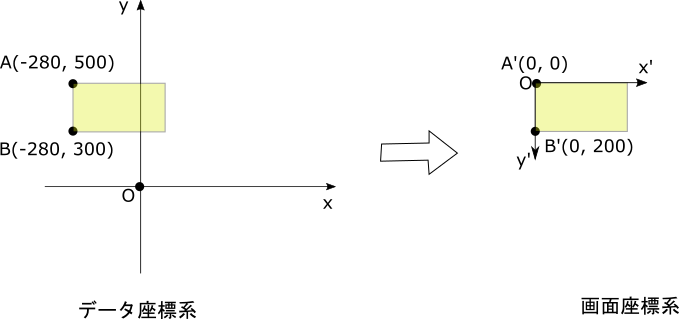
(x1, y1)を(-280, 500)としたときの図と各座標は次となります。
\begin{align*}
(A'_x, A'_y) &= (A_x - (-280), -(A_y - 500))\\
&= (A_x + 280, -A_y + 500)\\
&= (0, 0)\\
(B'_x, B'_y) &= (B_x - (-280), -(B_y - 500))\\
&= (B_x + 280, -B_y + 500)\\
&= (0, 200)
\end{align*}
このアフィン変換は、次のコードで作成されます。
Affine affine = new Affine(1, 0, 280, 0, -1, 500);
ちょっとわかりにくいですね。
2つの座標変換の組み合わせで考えてみます。
- 平行移動
- 上下反転
平行移動のアフィン変換は次の行列式で表されます。
\begin{pmatrix}
1 & 0 & -x_1\\
0 & 1 & -y_1\\
0 & 0 & 1
\end{pmatrix}
上下反転のアフィン変換は次の行列式で表されます。
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}
まず平行移動を実施して、次に上下反転をします。この場合、行列の結合では最初に適用する方を右側に書きます。
\begin{pmatrix}
1 & 0 & 0\\
0 & -1 & 0\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
1 & 0 & -x_1\\
0 & 1 & -y_1\\
0 & 0 & 1
\end{pmatrix}=
\begin{pmatrix}
1 & 0 & -x_1\\
0 & -1 & y_1\\
0 & 0 & 1
\end{pmatrix}
JDK 9のjshell環境でAffineの実験
2つのAffineを合成します。
jshell> Affine affineMove = new Affine(1, 0, -(-280), 0, 1, -500)
affineMove ==> Affine [
1.0, 0.0, 0.0, 280.0
0.0, 1.0, 0.0, -500.0
0.0, 0.0, 1.0, 0.0
]
jshell> Affine affineReverse = new Affine(1, 0, 0, 0, -1, 0)
affineReverse ==> Affine [
1.0, 0.0, 0.0, 0.0
0.0, -1.0, 0.0, 0.0
0.0, 0.0, 1.0, 0.0
]
jshell> affineReverse.createConcatenation(affineMove)
$35 ==> Affine [
1.0, 0.0, 0.0, 280.0
0.0, -1.0, 0.0, 500.0
0.0, 0.0, 1.0, 0.0
]
うーん、やはりわかりにくいです・・・。
さて、座標変換を実行してみます。
jshell> affine = new Affine(1, 0, 280, 0, -1, 500)
affine ==> Affine [
1.0, 0.0, 0.0, 280.0
0.0, -1.0, 0.0, 500.0
0.0, 0.0, 1.0, 0.0
]
jshell> Point2D dataJ = new Point2D(-280, 500)
dataJ ==> Point2D [x = -280.0, y = 500.0]
jshell> affine.transform(dataJ)
$29 ==> Point2D [x = 0.0, y = 0.0]
jshell> Point2D dataK = new Point2D(-280, 300)
dataK ==> Point2D [x = -280.0, y = 300.0]
jshell> affine.transform(dataK)
$30 ==> Point2D [x = 0.0, y = 200.0]
データ座標系の(-280, 500)が画面座標系の(0, 0)へ変換されました。
データ座標系の(-280, 300)が画面座標系の(0, 200)へ変換されました。
座標変換(その5):拡大縮小と平行移動
データ座標系の描画領域の大きさを任意の大きさに拡大または縮小させます。
拡大率を S とし、データ座標系上での描画領域の左上隅の座標を (x1, y1)とすると、次の式で拡大縮小と平行移動を表します。
\begin{align*}
x' &= s(x - x_1) = sx - sx_1\\
y' &= -s(y - y_1) = -sy + sy_1
\end{align*}
アフィン変換で表現すると次になります。
\begin{pmatrix}
x'\\y'\\1
\end{pmatrix}=
\begin{pmatrix}
s & 0 & -sx_1\\
0 & -s & sy_1\\
0 & 0 & 1
\end{pmatrix}
\begin{pmatrix}
x\\y\\1
\end{pmatrix}
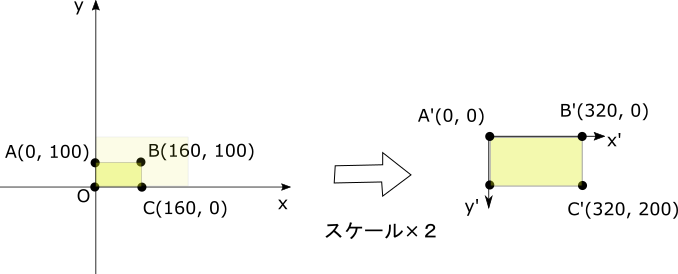
拡大率2、平行移動(0, 100)の場合
ここで、拡大率を2に、平行移動量を(0,100)とした場合のデータ座標系の表示領域と、画面座標系への変換を図で見てみます。
拡大率が2倍なので、データ座標系の中の160×100の範囲が画面座標系320×200に描画されます。
\begin{align*}
(A'_x, A'_y) &= (2A_x + 2・0, -2A_y + 2・100)\\
&= (0, 0)\\
(B'_x, B'_y) &= (2B_x + 2・0, -2B_y + 2・100)\\
&= (320, 0)\\
(C'_x, C'_y) &= (2C_x + 2・0, -2C_y + 2・100)\\
&= (320, 200)
\end{align*}
データのコンテンツは次の図のようになります。
このアフィン変換は、次のコードで作成されます。
Affine affine = new Affine(2, 0, 0, 0, -2, 200);
JDK 9のjshell環境でAffineの実験
jshell> affine = new Affine(2, 0, 0, 0, -2, 200)
affine ==> Affine [
2.0, 0.0, 0.0, 0.0
0.0, -2.0, 0.0, 200.0
0.0, 0.0, 1.0, 0.0
]
jshell> dataA = new Point2D(0, 100)
dataA ==> Point2D [x = 0.0, y = 100.0]
jshell> affine.transform(dataA)
$38 ==> Point2D [x = 0.0, y = 0.0]
jshell> dataB = new Point2D(160, 100)
dataB ==> Point2D [x = 160.0, y = 100.0]
jshell> affine.transform(dataB)
$40 ==> Point2D [x = 320.0, y = 0.0]
jshell> dataC = new Point2D(160, 0)
dataC ==> Point2D [x = 160.0, y = 0.0]
jshell> affine.transform(dataC)
$42 ==> Point2D [x = 320.0, y = 200.0]
データ座標系の(0, 100)が画面座標系の(0, 0)へ変換されました。
データ座標系の(160, 100)が画面座標系の(320, 0)へ変換されました。
データ座標系の(160, 0)が画面座標系の(320, 200)へ変換されました。
拡大率0.5、平行移動(100, 1000)での例
拡大率が0.5で平行移動量が(100,1000)のときの変換の図を次に示します。
このときのアフィン変換の行列は次になります。
\begin{pmatrix}
0.5 & 0 & -50\\
0 & -0.5 & 500\\
0 & 0 & 1
\end{pmatrix}
JDK 9のjshell環境でAffineの実験
jshell> Affine affine = new Affine(0.5, 0, -50, 0, -0.5, 500)
affine ==> Affine [
0.5, 0.0, 0.0, -50.0
0.0, -0.5, 0.0, 500.0
0.0, 0.0, 1.0, 0.0
]
jshell> affine.transform(100, 1000)
$4 ==> Point2D [x = 0.0, y = 0.0]
jshell> affine.transform(740, 1000)
$5 ==> Point2D [x = 320.0, y = 0.0]
jshell> affine.transform(740, 600)
$6 ==> Point2D [x = 320.0, y = 200.0]
jshell> affine.transform(100, 600)
$7 ==> Point2D [x = 0.0, y = 200.0]
jshell>
今回は、変換のインプットとしてPoint2Dインスタンスではなく直接x座標値、y座標値を入れてみました。
データ座標系の(100, 1000)が画面座標系の(0, 0)へ変換されました。
データ座標系の(740, 1000)が画面座標系の(320, 0)へ変換されました。
データ座標系の(740, 600)が画面座標系の(320, 200)へ変換されました。
データ座標系の(100, 600)が画面座標系の( 0, 200)へ変換されました。
座標変換(その6):画面中心で拡大縮小
これまでの座標変換における拡大・縮小では、画面左上を基点としています。
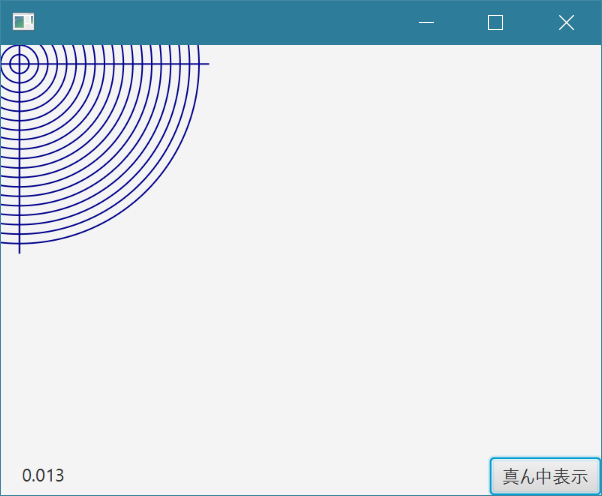
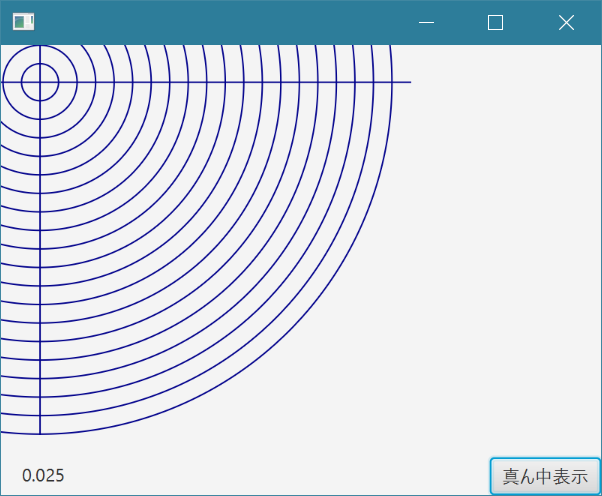
次に、ここまでの座標変換を実装したとあるCanvasのサンプルプログラムの表示を見てみます。表示(1)から表示(3)へ拡大していくと、左上隅を基点に表示されていることがわかります。
しかし、直感的な操作としては、画面中心を基点として拡大・縮小してほしいところです。
そこで、今回は画面座標系において画面左上隅の座標を画面中心に移動させる平行移動を追加することとします。
まず、「座標変換(その5):拡大縮小と平行移動」で使用した座標変換の式を次に再度挙げます。
\begin{align*}
x' &= sx - sx_1 \\
y' &= -sy + sy_1
\end{align*}
画面の幅をw, 画面の高さをhとします。画面左上隅を画面中心に平行移動する操作の座標変換式は次となります。
\begin{align*}
x'' &= x' + \frac{w}{2}\\
y'' &= y' + \frac{h}{2}
\end{align*}
画面左上隅を画面中心に平行移動する操作を追加した座標変換式は次となります。
\begin{align*}
x'' &= sx - sx_1 + \frac{w}{2}\\
y'' &= -sy + sy_1 + \frac{h}{2}
\end{align*}
画面のサイズに応じた平行移動は、データ座標系の拡大縮小には影響されないので、上の式のように拡大縮小係数sはかけられていません。
図を次に示します。
アフィン変換は次の行列式で表されます。
\begin{pmatrix}
s & 0 & -sx_1 + \frac{w}{2}\\
0 & -s & sy_1 + \frac{h}{2}\\
0 & 0 & 1
\end{pmatrix}
JDK 9のjshell環境でAffineの実験
画面サイズを320x200として、データ座標系での描画領域の左上隅座標を(200, 500)、スケールを2としたとき
jshell> affine = new Affine(2, 0, -240, 0, -2, 1100)
affine ==> Affine [
2.0, 0.0, 0.0, -240.0
0.0, -2.0, 0.0, 1100.0
0.0, 0.0, 1.0, 0.0
]
jshell> affine.transform(200, 500)
$12 ==> Point2D [x = 160.0, y = 100.0]
とデータ座標系の左上隅(200, 500)が画面座標系での(160, 100)と画面中心に変換されたことがわかります。
画面サイズを320x200として、データ座標系での描画領域の左上隅座標を(200, 500)、スケールを0.5としたとき
jshell> affine = new Affine(0.5, 0, 60, 0, -0.5, 350)
affine ==> Affine [
0.5, 0.0, 0.0, 60.0
0.0, -0.5, 0.0, 350.0
0.0, 0.0, 1.0, 0.0
]
jshell> affine.transform(200, 500)
$14 ==> Point2D [x = 160.0, y = 100.0]
とデータ座標系の左上隅(200, 500)が画面座標系での(160, 100)と画面中心に変換されたことがわかります。
まとめ
右手系の直交座標系で定義されるデータを画面に表示する際に使用するアフィン変換は、次のとおりです。
\begin{pmatrix}
s & 0 & -sx_1 + \frac{w}{2}\\
0 & -s & sy_1 + \frac{h}{2}\\
0 & 0 & 1
\end{pmatrix}
但し、\\
sは拡大率\\
(x_1, y_1)は画面の中心に表示するデータ座標\\
(w, h)は画面座標系における表示サイズの幅と高さ
参考・関連情報
このアフィン変換を使用したJavaFX Canvasでの画面表示サンプルプログラムとその解説を次に記載しています。
本記事を書くきっかとなったJJUG CCC 2016 Fallでの発表スライドは次です。
過去にCanvasでのアフィン変換に取り組みはまったことを書いたブログ