はじめに
「量子コンピュータができたら暗号が解かれてヤバい」なんて話を聞いたことは無いでしょうか。
量子コンピュータは因数分解を高速に解けるので、現在の暗号システムはすぐに破られてしまう、などと言われていますね。
今回はその暗号を解くために必要な因数分解についての話をします。
厳密な理論とかいいから、イメージだけ知りたいって人向けにゆるくまとめます。
因数分解の解き方
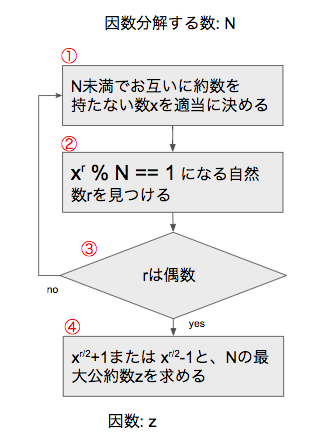
因数分解のための定番アルゴリズムがありまして、量子コンピュータでも同じものを使います。
フローチャートを貼っておきますが、最悪内容は分からなくても番号だけ覚えてもらえれば大丈夫です。
高速に解けない原因
フローチャートの各項目に①〜④の番号を付けておきました。大きく分けて4つ項目があるわけですが、実は
① 条件付きで乱数を生成するだけ
③ ただのif文
④ ユークリッドの互除法を使えば四則演算で解ける
ですので、②以外はサクッと計算できるものばかりなんですね。
ところが、②の計算時間は、因数分解する数の桁が1つ増えれば10倍、2つ増えれば100倍と、指数関数的に増えていきます。
②の求め方としてすぐに思いつくのは、しらみ潰しに全部の自然数を確認していく方法です。
しかし、上記のようにこれではすぐに計算量が爆発的に増えてしまいます。
そこで、少し工夫が必要です。
rを求めたい
②を解くために、余剰の周期性を利用します。
イメージしやすいようにPythonコードで具体的な例を出すと、x = 4, N = 25として
4**1 % 25 # => 4
4**2 % 25 # => 16
4**3 % 25 # => 14
4**4 % 25 # => 6
4**5 % 25 # => 24
4**6 % 25 # => 21
4**7 % 25 # => 9
4**8 % 25 # => 11
4**9 % 25 # => 19
4**10 % 25 # => 1
4**11 % 25 # => 4
4**12 % 25 # => 16
4**13 % 25 # => 14
4**14 % 25 # => 6
4**15 % 25 # => 24
4**16 % 25 # => 21
4**17 % 25 # => 9
4**18 % 25 # => 11
4**19 % 25 # => 19
4**20 % 25 # => 1
4**21 % 25 # => 4
4**22 % 25 # => 16
4**23 % 25 # => 14
4**24 % 25 # => 6
4**25 % 25 # => 24
4**26 % 25 # => 21
4**27 % 25 # => 9
4**28 % 25 # => 11
4**29 % 25 # ...
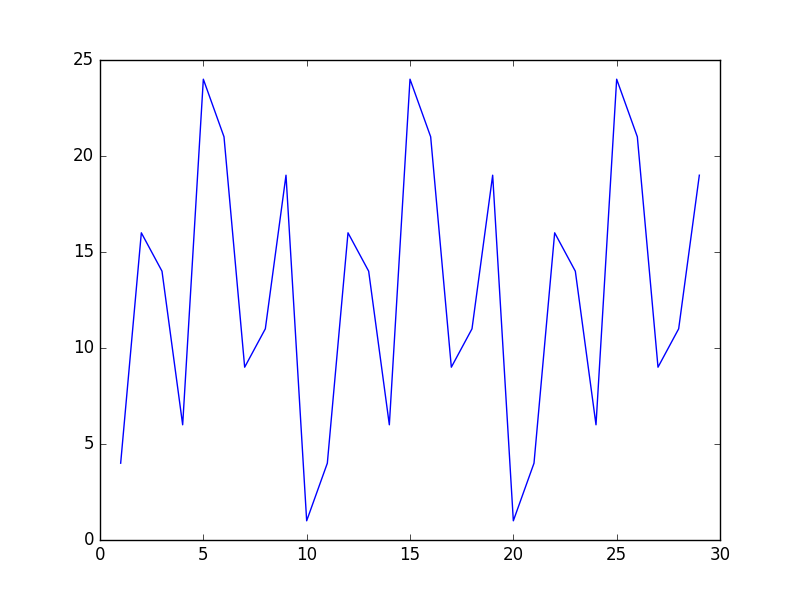
同じパターンが繰り返されています。
グラフにしてみるとこんな感じです。周期があるのがわかりますね。
この周期が分かれば、②を満たす自然数rを求める事ができます。
周期を求めると言えば
あるパターンから周期を求めるには、「フーリエ変換」がよく使われます。
フーリエ変換は奥が深くて重要な分野なのですが、詳しく話すにはどうしても数学的に難しくなるので、今回は使うとどうなるのか結果だけお見せします。
さっきの余剰のグラフの式をフーリエ変換すると、次のようになります。なんか城みたいなグラフですね。
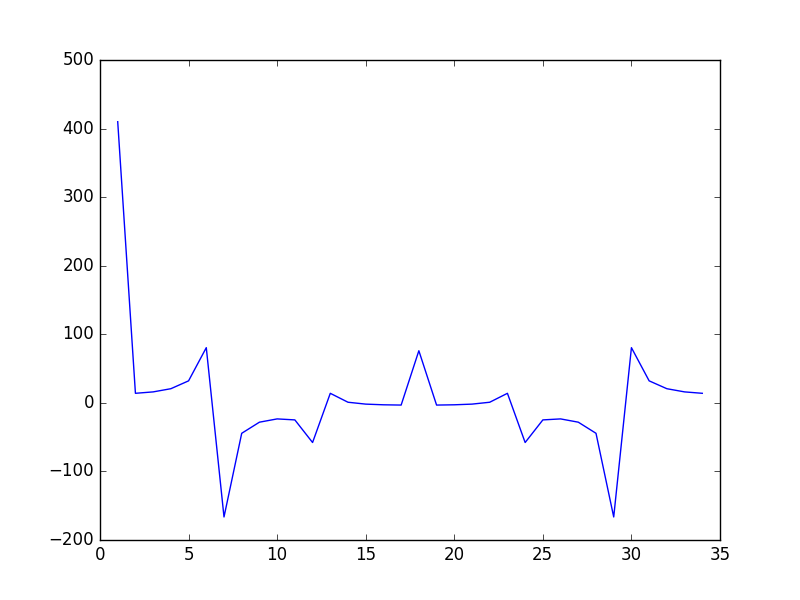
この中で尖ってる偶数をrとして使用します。
今回は3つありますが、どれでもいいので6を使うことにします。
これでrを求められたので、あとは簡単に因数を求める事ができます。
math.gcd(int(4**(6/2)+1), 25) # 5
こうして因数5が求められました。
このようにフーリエ変換を使えば因数を求められるのですが、従来のコンピュータはフーリエ変換も苦手です。
条件にもよりますが、最悪の場合はrをしらみ潰しに探した方が早いくらい苦手です。
ところが、量子コンピュータならフーリエ変換を高速に解けます。
どのくらい差があるかというと、従来のコンピュータで100桁の数字をフーリエ変換するなら、2の100乗回の操作が必要です。
数字で書くと1000000000000000000000000000000回です。
対して量子コンピュータならだいたい5000回で計算できます。
量子コンピュータの場合は何度か計算をやり直さなければいけない場合もあるのですが、それを差し引いても圧倒的な差ですね。
このフーリエ変換を高速に解けるという性質が、因数分解の高速な計算を可能にしています。
サンプル
projectQというライブラリで、今回紹介した量子アルゴリズムのExampleが用意されています。
https://github.com/ProjectQ-Framework/ProjectQ/blob/develop/examples/shor.py
projectQをインストールしているなら、gitからcloneしてpython shor.pyすれば試してみる事ができます。
あくまでシミュレータなので全く高速ではありませんが、コードを見てみると理解が深まるかもしれません。
まとめ
最後に要約すると、
因数分解はフーリエ変換に時間がかかる
でも量子コンピュータはフーリエ変換を高速に解ける
だから量子コンピュータは高速に因数分解できる
です。
フーリエ変換を高速に解けるなら、他にもいろいろな事に応用できそうな気がしますね。